Система относительных единиц

ТРЁХФАЗНОЕ КОРОТКОЕ ЗАМЫКАНИЕ В ЭЛЕКТРИЧЕСКОЙ СЕТИ

Все физические величины являются именованными. Представление их в относительных единицах (или процентах) позволяет упростить теоретические выкладки и придать им более общий характер. Поэтому относительные единицы широко используются в курсах «Электрические машины» и «Электромагнитные переходные процессы в энергетических системах».

Под относительным значением физической величины понимают её отношение к другой одноимённой физической величине, выбранной за единицу измерения, т.е. базисную величину (или базу). Относительные величины обозначают нижним индексом "_*" (звёздочка).

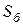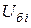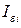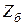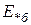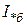В качестве базисных величин в расчётах часто принимают базисные мощность ( ), напряжения ( ), токи ( ), сопротивления ( ). Базисные величины обозначают нижним индексом "б". В этом случае относительные единицы называют относительными базисными, например, ЭДС , ток и т.п. Таким образом, относительные базисные единицы определяются следующими выражениями:

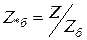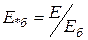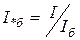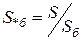, , , и т.п.

За единицу измерения угловых скоростей обычно принимают синхронную угловую скорость 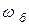, т.е. 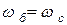. Тогда произвольная угловая скорость в относительных единицах будет:

.

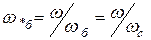Соответственно этому в качестве базисных единиц принимают:

· для индуктивности

;

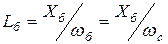· для потокосцепления

,

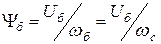т.е. потокосцепление, индуктирующее при базисной угловой скорости базисное напряжение.

Таким образом, при указанных базисных единицах и 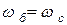, имеем

,

,

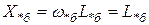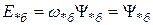т.е. в относительных единицах индуктивное сопротивление равно индуктивности, а ЭДС – потокосцеплению.

Фазное напряжение в относительных базисных единицах

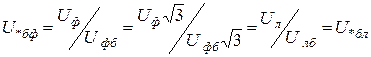
равно линейному относительному базисному. Аналогично в относительных единицах амплитудное значение равно действующему

.

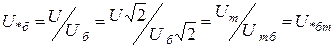Из этих выражений можно также установить, что в относительных единицах мощность одной фазы равна мощности трёх фаз; ток возбуждения, поток и ЭДС генератора численно равны между собой.

Необходимо отметить также, что для любого элемента электрической сети относительное сопротивление равно относительному падению напряжения при протекании через него номинального тока (или мощности).

При выполнении расчётов токов КЗ используются четыре базисных параметра: мощность, напряжение, ток и сопротивление. Базисные мощность и напряжение принимают независимыми, через которые выражаются базисные ток и сопротивление. Из уравнения мощности трёхфазной цепи

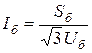, (1.1)

а на основании закона Ома для трёхфазной цепи

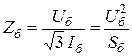. (1.2)

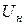Поскольку выбор базисных величин произволен, то одна и та же физическая величина может иметь разные численные значения при выражении её в относительных единицах. Обычно относительные значения сопротивлений элементов энергосистем: генераторов, трансформаторов, двигателей задаются в относительных номинальных единицах при номинальных параметрах: и (номинальные величины обозначают нижним индексом "н"). При этом относительные номинальные единицы записываются в виде

, , , , .

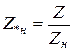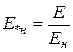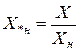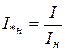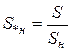Номинальный ток 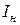и сопротивление 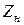можно найти с помощью выражений, аналогичных (1.1) и (1.2)

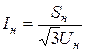, (1.3)

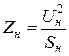. (1.4)

Установим связь между именованными величинами и относительными единицами. По определению, относительная базисная величина определяется выражением

,

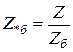подставив в последнее выражение формулу (1.2), получим

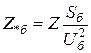(1.5)

С помощью выражения (1.5) осуществляется перевод именованных величин в относительные базисные.

Аналогично для относительных номинальных единиц с учётом (1.4), получим

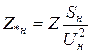. (1.6)

Выражение (1.6) наиболее часто используется для вычисления сопротивлений в именованных единицах, при известных относительных номинальных, в следующем виде

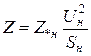. (1.7)

Подставив в (1.5) значение 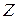из выражения (1.7), получим выражение, которое устанавливает связь между относительными номинальными и относительными базисными единицами

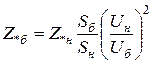. (1.8)

Выражение (1.8) используется для перевода относительных номинальных единиц в относительные базисные.

Для ограничения ТКЗ в энергосистемах используются токоограничивающие реакторы, представляющие собой линейные индуктивности. Для реакторов задаются номинальный ток (а не мощность) и напряжение.

Учитывая, что 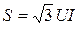выражения (1.6) и (1.8) преобразуются соответственно

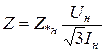(1.9)

и

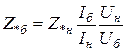. (1.10)

Относительные величины выражаются также и в процентах, например, сопротивление .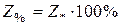

ЛЕКЦИЯ 2