Метод симметричных составляющих

2.1.1 Основные понятия метода симметричных составляющих.

Метод симметричных составляющих базируется на теории многофазных электрических систем при неодинаковых условиях работы фаз. Математическое обоснование метода было разработано К. Фортескью (C.L. Fortescue), а затем Р.Д. Эванс (R. Evans) и К.Ф. Вагнер (C. Wagner) применили его для анализа несимметричных коротких замыканий. В нашей стране большую роль во внедрении МСС в расчётную практику сыграли работы Николая Николаевича Щедрина и Сергея Александровича Ульянова.

Основная идея МСС заключается в следующем. В декартовой системе координат любой вектор имеет две степени свободы и может быть представлен через его проекции в виде

.

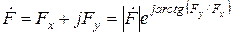Отсюда следует, что любая система из трёх несимметричных векторов имеет шесть степеней свободы. Несимметричную систему из трёх векторов можно представить в виде трёх симметричных систем, каждая из которых имеет две степени свободы. Исходя из физической картины явлений в электрических системах, используют три симметричных системы: прямой, обратной и нулевойпоследовательностей. Для каждой из этих систем явления в фазах подобны, что позволяет воспользоваться однолинейными схемами для каждой последовательности и вести расчёт для одной фазы. Такая фаза находится в условиях, отличающихся от условий для двух других фаз, и называется особой фазой. В этом заключается одно из главных достоинств МСС.

Разложение несимметричной трёхфазной системы произвольных векторов 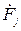( 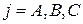) на три симметричных системы векторов прямой (1), обратной (2) и нулевой (0) последовательностей и чередование фаз в них показано на рис.2.1:

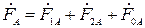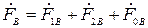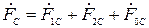; ; . (2.1)

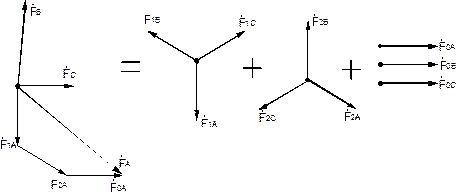
Рис.2.1. Разложение несимметричной системы векторов на три симметричные

Любой из векторов симметричной трёхфазной системы можно представить одноимённым вектором другой фазы с помощью оператора фазы (поворота) а:

.

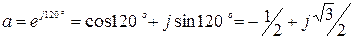Таким образом, оператор фазы является вектором, модуль которого равен единице, а аргумент 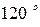. При умножении вектора на оператор фазы, происходит поворот исходного вектора на 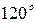в положительном направлении (против часовой стрелки) без изменения его длины.

Основные свойства оператора фазы:

, ,

, .

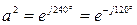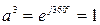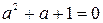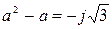Введение оператора фазы позволяет выразить два вектора каждой симметричной системы (2.1) через третий вектор той же системы, например, через вектор ( ).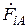

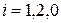В симметричной трёхфазной системе прямой последовательности каждый из векторов можно представить следующими выражениями:

; ; .

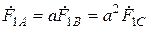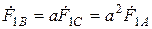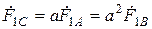Подобные выражения можно записать и для обратной последовательности

; ; .

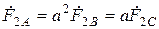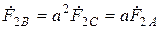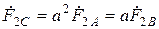Систему уравнений (2.1) можно представить в виде:

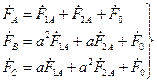, (2.2)

при этом .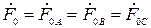

Компактно система уравнений (2.2) записывается в матричной форме

,

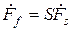где 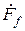− вектор фазных (несимметричных) величин; 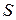− матрица Фортескью (коэффициентов симметричных составляющих); 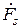− вектор симметричных составляющих.

Используя обратное преобразование можно получить

,

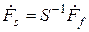где 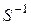- обратная матрица Фортескью:

.

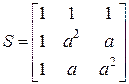
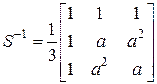Ротор любой реальной синхронной машины, даже турбогенератора, не обладает полной магнитной и электрической симметрией. Поэтому при несимметричном режиме синхронной машины, как в токе статора, так и в токе обмотки возбуждения возникают высшие гармонические составляющие. Токи различных последовательностей оказываются связанными между собой через бесконечный спектр гармоник. Полный спектр гармоник токов в синхронной машине возникает в результате несимметрии токов в фазах и несимметрии самой синхронной машины.

Однако при наличии демпферных контуров в обеих осях ротора синхронной машины (у турбогенераторов роль демпферных контуров выполняет стальной массив ротора) степень несимметрии ротора незначительна. Поэтому при несимметричных режимах таких машин высшие гармонические составляющие проявляются незначительно.

В связи с этим в практических расчётах учитывают только основные гармоники токов и напряжений, что в большинстве случаев является приемлемым с точки зрения допустимой погрешности. Использование только основных гармоник позволяет распространить МСС и для анализа переходных процессов при несимметричных КЗ.

Решение системы уравнений (2.2) даёт формулы для определения симметричных составляющих

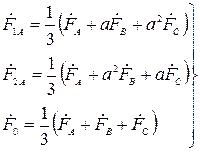. (2.3)

Системы уравнений (2.2) и (2.3) однозначно устанавливают связь между фазными величинами и их симметричными составляющими и являются основными уравнениями метода симметричных составляющих. Приведенные выражения справедливы для всех электрических векторов, например, токов, напряжений, ЭДС и т.п.

Поскольку векторы системы прямой (обратной) последовательности в сумме равны нулю, эти системы являются уравновешенными

,

.

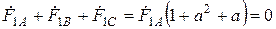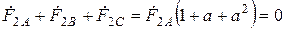Система нулевой последовательности состоит из трёх одинаковых векторов, совпадающих по направлению. Эта система симметрична, но не уравновешена:

.

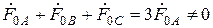Степень несимметрии системы векторов характеризуется коэффициентом несимметрии 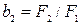, а степень неуравновешенности - коэффициентом неуравновешенности 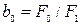. В нормальном симметричном режиме и при трёхфазном КЗ 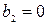и .

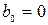При замыкании на землю в токах и напряжениях содержатся составляющие прямой, обратной и нулевой последовательностей; при междуфазных замыканиях только прямой и обратной.

2.1.2 Схемы замещения отдельных последовательностей. Сущность метода симметричных составляющих заключается в том, что если учитываются только основные гармоники токов и напряжений, то составляющие разноимённых последовательностей между собой не взаимодействуют. Это позволяет изображать схемы замещения отдельно для каждой последовательности.

Источники ЭДС (синхронные генераторы, электрические системы, электрические двигатели в начальный момент КЗ) являются источниками ЭДС прямой последовательности; источников ЭДС обратной и нулевой последовательностей нет (они равны нулю).

Ниже приведены рекомендации по составлению схем замещения отдельных последовательностей.

Схема замещения прямой последовательности (СЗПП). Эта схема имеет такую же структуру и параметры элементов, как и схема замещения при трёхфазном КЗ; но отличается от неё только тем, что в место повреждения включён источник напряжения прямой последовательности 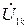. Симметричные составляющие в электрической сети появляются в результате разложения несимметричной системы векторов на симметричные составляющие.

Схема замещения обратной последовательности (СЗОП). Схема имеет такую же структуру и параметры элементов, как и схема замещения при трёхфазном КЗ, за исключением элементов с подвижными магнитосвязанными цепями (генераторы, электрические двигатели, синхронные компенсаторы); источники ЭДС генераторов закорочены (их сопротивления в течение переходного процесса не изменяются); в место повреждения включён источник напряжения обратной последовательности 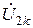. Для всей схемы замещения обратной последовательности, как правило, 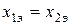, поэтому при выполнении производственных расчётов схемы замещения обратной последовательности иногда не изображают.

Схемы замещения нулевой последовательности (СЗНП) обычно значительно отличаются от схем замещения прямой (обратной) последовательности, так как отличаются пути протекания тока нулевой последовательности 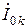от путей протекания токов прямой (обратной) последовательности.

Составление схемы замещения нулевой последовательности рекомендуется начинать с точки КЗ, в которую включают источник напряжения нулевой последовательности 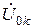.Условием для протекания тока нулевой последовательности является наличие элементов с заземлёнными нейтралями электрически связанных с точкой КЗ.

Схемам замещения прямой, обратной и нулевой последовательностей соответствуют первое, второе и третье уравнение системы соответственно:

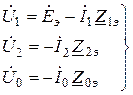, (2.4)

где 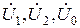- напряжения прямой, обратной и нулевой последовательности в точке КЗ в схемах замещения прямой, обратной и нулевой последовательности соответственно, 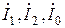- токи прямой, обратной и нулевой последовательностей, 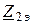, 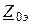- суммарные сопротивления прямой, обратной и нулевой последовательностей, 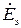- суммарная (эквивалентная) ЭДС (за положительное направление тока принимается направление к месту повреждения). Система уравнений (2.4) записана для установившегося синусоидального режима, однако в операторной форме справедлива и для переходного режима.

ЛЕКЦИЯ 8