Согласование источника заявок с каналом обслуживания
Способы согласованияподразделяются на два основных вида.
1) Синхронный способ. Используется при постоянной скорости поступления заявок. Моменты поступления заявок совпадают с моментами их передачи на обслуживание в канал обслуживания. При этом обслуживающий аппарат может простаивать или отклонять заявки.
2) Асинхронный способ. Используется при неравномерном поступлении заявок с целью избежать их потери. Для реализации необходим буферный накопитель, сглаживающий неравномерность поступления заявок. Главной задачей здесь является выбор емкости буферного накопителя, который основан на оценке средней длины очереди L. При этом используются введенные выше характеристики, такие как среднее время ожидания и среднее время обслуживания. Также используется показатель относительного ухудшения времени обслуживания за счет других заявок:
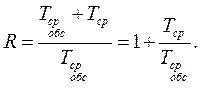
Случай согласования простейшего пуассоновского источника заявок с каналом с показательным законом распределения времени обслуживания (случай 1)
Случай 1. Пусть на вход системы поступает простой поток заявок, т.е. ν(t)=λt, а время обслуживания распределяется по экспоненциальному закону, т.е. F*(t)=1–exp(–μt).
Пусть также r £ 1. В этом случае обслуживающий прибор справляется с загрузкой, и возникает установившийся процесс обслуживания.
Тогда справедливо следующее выражение:
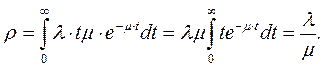
Известна следующая теорема. За время прохождения заявкой очереди от конца к началу длина очереди остается постоянной и равной числу заявок, пришедших за время ожидания, т.е.
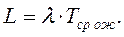

 Здесь
Здесь
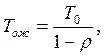
где T0 – среднее время, необходимое для завершения начатого обслуживания одной заявки при экспоненциальном законе распределения времени обслуживания.
 |  |  |  |
Вообще
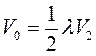
и
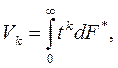
откуда
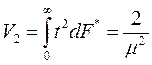
и
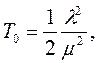
следовательно
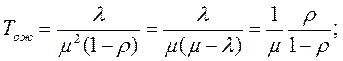
теперь можно найти длину очереди:
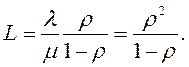
Случай согласования простейшего пуассоновского потока заявок с каналом с постоянным временем обслуживания (случай 2)
Случай 2. Пусть на вход системы поступает простейший пуассоновский поток заявок, а время обслуживания постоянно: Т=Тобсл.
Функция распределениявремени обслуживания в этом случае имеет вид, показанный на рисунке 5.10. (см. Приложение 3).
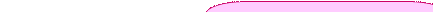
Рис. 5.10. Функция распределения в случае постоянного времени обслуживания
F*(t)=1[t – Tобсл] – это уже не случайная функция! Такое распределение называется вырожденным.
Плотность распределения w*(t) в этом случае есть производная от единичной ступенчатой функции, т.е. дельта-функция δ[t-Tобсл], смещенная относительно начала координат вправо по оси времени на величину Tобсл (рис. 5.11).

Рис. 5.11. К стробирующему свойству дельта-функции Дирака
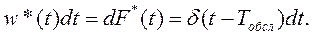
Используется стробирующее свойство δ-функции:

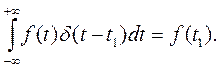
В данном случае загрузка обслуживающего прибора будет равна:
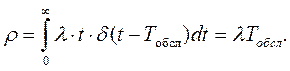
Дата добавления: 2021-09-07; просмотров: 430;











