ТЕПЛООБМЕН МЕЖДУ ТЕЛАМИ, РАЗДЕЛЕННЫМИ ПРОЗРАЧНОЙ СРЕДОЙ
Постановка задачи и общий метод расчета.
При проведении инженерных расчетов лучистого теплообмена между телами, разделенными прозрачной (диатермичной) средой, приходится вводить ряд упрощений. Наиболее широко распространено предположение о том, что поверхности излучения – серые, их эффективное излучение является диффузным (энергия отражается равномерно по всем направлениям) и характеризуется неизменной плотностью на изотермических участках поверхностей системы.
При таких приближениях для проведения расчетов требуется минимальная исходная информация: необходимо знать интегральные коэффициенты теплового излучения поверхностей системы и размещение тел в пространстве.
Типовая задача
Имеется замкнутая система известной геометрии, состоящая из N изотермических поверхностей, имеющих температуры Ti и коэффициенты теплового излучения 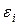 (i=1, 2, ... , N). Требуется рассчитать лучистый теплообмен в такой системе, т.е. найти результирующие лучистые потоки Ерезi для каждой поверхности.
(i=1, 2, ... , N). Требуется рассчитать лучистый теплообмен в такой системе, т.е. найти результирующие лучистые потоки Ерезi для каждой поверхности.
Ерезi = Есобсi - Епад= Есобсi-Аi* Епад
Метод решения.
Напомним, определение результирующего и эффективного излучения.
Эффективное излучение – это сумма собственного и отраженного излучения (излучения, которое регистрирует прибор).
Еэф1=Е1+(1-А1)Епад, (1)
где А1-коэффициент поглощения;
Е1-собственное излучение.
Результирующее излучение- разность между собственным и поглощенным излучением (показывает расход или приход энергии вследствие лучистого теплообмена с окружающей средой):
Ерезi=E1-A1Eпад
Из этих определений после исключения величины потока падающего излучения, получаем
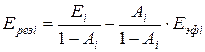 (3)
(3)
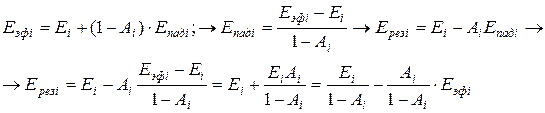
Это соотношение связывает собственное, эффективное и результирующее излучения для данной поверхности.
Известно (из закона Стефана-Больцмана), что собственное излучения для серых тел
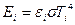 , где
, где
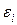 - интегральный коэффициент теплового излучения;
- интегральный коэффициент теплового излучения;
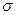 - постоянная Стефана-Больцмана
- постоянная Стефана-Больцмана
Из закона Кирхгофа – коэффициенты теплового поглощения и излучения равны, т.е.
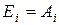
Тогда равенство (3) принимает вид
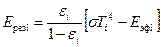 (3’)
(3’)
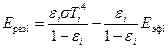
Следовательно, если известны эффективные потоки 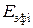 излучения в системе, то можно определить искомые результирующие потоки
излучения в системе, то можно определить искомые результирующие потоки 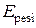 .
.
Выражения для эффективных потоков для каждой поверхности можно представить в виде
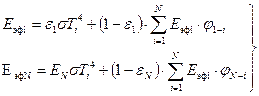
 (4)
(4)
В правой части этих соотношений первые слагаемые представляют потоки собственного излучения; суммы характеризуют потоки излучения, падающего на соответствующие поверхности; они же, умноженные на 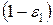 дают потоки отраженного излучения.
дают потоки отраженного излучения.
В соотношении (4) 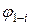 ,
, 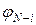 - угловые коэффициенты – геометрические характеристики пространственного расположения тел. Методы расчета этих коэффициентов рассмотрели ниже.
- угловые коэффициенты – геометрические характеристики пространственного расположения тел. Методы расчета этих коэффициентов рассмотрели ниже.
Итак, при известных угловых коэффициентах соотношения (4) образуют систему из N линейных алгебраических уравнений относительно N неизвестных величин 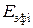 (i=1,…,N). Решение системы с учетом (3’) дает решение задачи.
(i=1,…,N). Решение системы с учетом (3’) дает решение задачи.
На практике возможны и иные постановки задачи. Например, известны 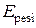 , а необходимо определить температуры поверхностей Ti. Может быт и смешанная задача. Но во всех случаях решение получается на базе приведенных алгебраических соотношений (3’) и (4).
, а необходимо определить температуры поверхностей Ti. Может быт и смешанная задача. Но во всех случаях решение получается на базе приведенных алгебраических соотношений (3’) и (4).
Угловые коэффициенты.
Угловой коэффициент 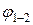 - показывает, какая доля от всего лучистого потока, излучаемого с поверхности F1 абсолютно черного изотермического излучателя 1 во все стороны пространства, достигает поверхности F2 тела 2, известным образом расположенного относительно 1 в пространстве.
- показывает, какая доля от всего лучистого потока, излучаемого с поверхности F1 абсолютно черного изотермического излучателя 1 во все стороны пространства, достигает поверхности F2 тела 2, известным образом расположенного относительно 1 в пространстве.
Угловые коэффициенты – положительные безразмерные числа, меньше 1 – они отражают лишь чисто геометрические особенности размещения 2-х тел в пространстве.
Угловые коэффициенты каждого из N тел, образующих замкнутую систему, обладают свойством замыкаемости:
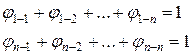
или в компактной форме 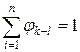
Это свойство вытекает из балансового соотношения для каждой поверхности, входящей в замкнутую систему.
Коэффициенты 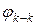 - учитывают излучения тела k на себя (самооблучение), что возможно, если тело k вогнутое. Для вогнутых m плоских тел
- учитывают излучения тела k на себя (самооблучение), что возможно, если тело k вогнутое. Для вогнутых m плоских тел 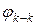 =0.
=0.
В общем виде в аналитической форме решение для углового коэффициента имеет простой вид лишь для определенного типа поверхностей. Имеются специальные диаграммы для определения угловых коэффициентов.
Дата добавления: 2021-09-07; просмотров: 819;











