Исследование функций с помощью производных: Достаточные признаки существования экстремумов. Выпуклость и вогнутость графика функции. Асимптоты
1. Первый и второй достаточные признаки существования экстремума.
Первый достаточный признак существования экстремума дается теоремой:
Т1. Если функция 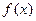 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки  , кроме может быть самой точки
, кроме может быть самой точки  , и при переходе через эту точку слева направо ее первая производная меняет свой знак с “+” на “–”, то в точке
, и при переходе через эту точку слева направо ее первая производная меняет свой знак с “+” на “–”, то в точке  функция
функция 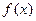 имеет максимум, а если ее первая производная меняет свой знак с “–” на “+”, то в точке
имеет максимум, а если ее первая производная меняет свой знак с “–” на “+”, то в точке  функция
функция 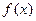 имеет минимум. Если при переходе через точку
имеет минимум. Если при переходе через точку  первая производная не меняет свой знак, то в этой точке экстремума нет.
первая производная не меняет свой знак, то в этой точке экстремума нет.
Второй достаточный признак существования экстремума дается теоремой:
Т2. Если в точке  первая производная функци
первая производная функци 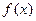 обращается в ноль (
обращается в ноль ( 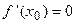 ), а вторая производная существует, непрерывна в некоторой окрестности этой точки и отлична от нуля в самой точке (
), а вторая производная существует, непрерывна в некоторой окрестности этой точки и отлична от нуля в самой точке ( 
 ), то в точке
), то в точке  наблюдается экстремум. Если при этом
наблюдается экстремум. Если при этом  , то точка
, то точка  является точкой минимума, а при
является точкой минимума, а при 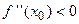 – точкой максимума.
– точкой максимума.
Пример 4. Найти и определить тип экстремумов функции  .
.

 Вычислим первую производную функции и приравняем ее к нулю с целью отыскания критических точек:
Вычислим первую производную функции и приравняем ее к нулю с целью отыскания критических точек: 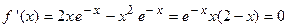 . Так как показательная функция
. Так как показательная функция  , то
, то 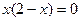 . Отсюда находим критические точки
. Отсюда находим критические точки 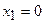 и
и 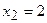 . Отложим эти точки на числовой оси и на каждом интервале определим знак первой производной функции, т.е. применим первый достаточный признак существования экстремума:
. Отложим эти точки на числовой оси и на каждом интервале определим знак первой производной функции, т.е. применим первый достаточный признак существования экстремума:



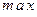
 |
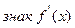 – 0 + 2 –
– 0 + 2 – 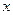
При переходе слева направо через точку 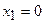 первая производная функция меняет свой знак с “–” на “+”, следовательно, в этой точке наблюдается минимум. При переходе слева направо через точку
первая производная функция меняет свой знак с “–” на “+”, следовательно, в этой точке наблюдается минимум. При переходе слева направо через точку 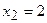 первая производная функция меняет свой знак с “+” на “–”, следовательно, в этой точке наблюдается максимум. Применим второй достаточный признак существования экстремума, для чего вычислим вторую производную функции:
первая производная функция меняет свой знак с “+” на “–”, следовательно, в этой точке наблюдается максимум. Применим второй достаточный признак существования экстремума, для чего вычислим вторую производную функции: 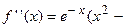
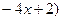 . Вычислим значение второй производной функции в точке
. Вычислим значение второй производной функции в точке 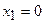 :
:  , следовательно, в этой точке функция имеет минимум. Вычислим значение второй производной функции в точке
, следовательно, в этой точке функция имеет минимум. Вычислим значение второй производной функции в точке 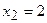 :
: 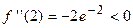 , следовательно, в этой точке функция имеет максимум.
, следовательно, в этой точке функция имеет максимум.
2. Наименьшее и наибольшее значения функции на сегменте 
1. Находят область определения функции и убеждаются в том, что заданный сегмент входит в эту область.
2. Находят критические точки, для чего решают уравнение  , и точки, в которых первая производная функции не существует.
, и точки, в которых первая производная функции не существует.
3. Вычисляют значения функции в критических точках, принадлежащих заданному сегменту, в точках, в которых первая производная функции не существует и на концах заданного сегмента.
4. Из полученных чисел выбирают наименьшее 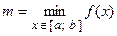 и наибольшее
и наибольшее 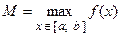 .
.
Пример 5. Найти наименьшее и наибольшее значения функции  на сегменте
на сегменте 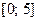 .
.
Действуя согласно вышеприведенной схеме, находим:
1.  . Следовательно, функция определена и непрерывна на заданном сегменте.
. Следовательно, функция определена и непрерывна на заданном сегменте.
2. Вычислим первую производную  . Производная существует на всей числовой оси, поэтому найдем критические точки
. Производная существует на всей числовой оси, поэтому найдем критические точки 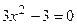 . Отсюда находим, что
. Отсюда находим, что 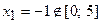 и
и 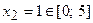 .
.
3. Вычислим значение функции в критических точках и на концах заданного сегмента: 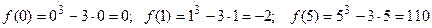 .
.
4. Из полученных чисел выбираем наименьшее 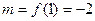 и наибольшее
и наибольшее  , которые определяют наименьшее и наибольшее значения функции
, которые определяют наименьшее и наибольшее значения функции  на сегменте
на сегменте 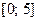 .
.
Дата добавления: 2021-09-07; просмотров: 485;











