Примеры решения задач. Определить реакции заделки

Пример 1. Одноопорная (защемленная) балка нагружена со­средоточенными силами и парой сил (рис. 6.7). Определить реакции заделки.

Решение

2. В заделке может возникнуть реакция, представляемая двум: составляющими (R_Ay,R_Ax), и реактивный момент М_A. Наносим на схему балки возможные направления реакций.

Замечание. Если направления выбраны неверно, при расчетах получим отрицательные значения реакций. В этом случае реакции на схеме следует направить в противоположную сторону, не повторяя расчета.

В силу малой высоты считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке. Для решения удобно использовать систему уравнений равновесия в первой форме. Каждое уравнение будет содержать одну неизвестную.

3. Используем систему уравнений:

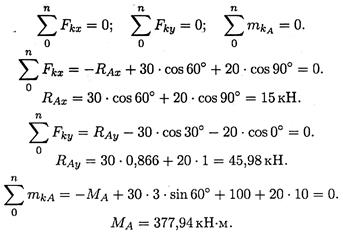
Знаки полученных реакций (+), следовательно, направления ре­акций выбраны верно.

3. Для проверки правильности решения составляем уравнение моментов относительно точки В.

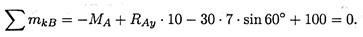
Подставляем значения полученных реакций:

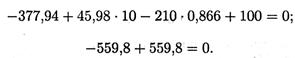
Решение выполнено верно.

Пример 2. Двухопорная балка с шарнирными опорами А и В нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой сил с моментом т (рис. 6.8а). Определить реакции опор.

Решение

1. Левая опора (точка А) — подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности.

Правая опора (точка В) — неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки.

2. Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецеле­сообразно.

3. Заменяем распределенную нагрузку сосредоточенной:

G = ql; G = 2*6 = 12 кН.

Сосредоточенную силу помещаем в середине пролета, далее за­дача решается с сосредоточенными силами (рис. 6.8, б).

4. Наносим возможные реакции в опорах (направление произвольное).

5. Для решения выбираем уравнение равновесия в виде

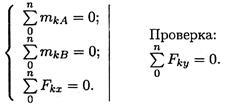
6. Составляем уравнения моментов относительно точек крепления:

Реакция отрицательная, следовательно, R_Аy нужно направить н противоположную сторону.

7. Используя уравнение проекций, получим:

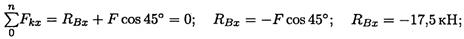
R_Bx — горизонтальная реакция в опоре В.

Реакция отрицательна, следовательно, на схеме ее направление будет противоположно выбранному.

8. Проверка правильности решения. Для этого используем чет­вертое уравнение равновесия

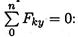
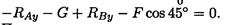
Подставим полученные значения реакций. Если условие выполнено, решение верно:

-5,1 - 12 + 34,6 – 25 -0,7 = 0.

Пример 3. Опреде­лить опорные реакции балки, показанной на рис. 1.17, а.

Решение

Рассмотрим рав­новесие балки АВ. Отбросим опорное закрепление (задел­ку) и заменим его действие реакциями Н_А,V_A и т_А (рис. 1.17, б). Получили плоскую систему произвольно распо­ложенных сил.

Выбираем систему координат (рис. 1.17,6) и состав­ляем уравнения равновесия:

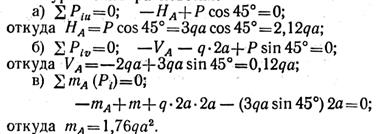
Составим проверочное уравнение

следовательно, реакции определены верно.

1. Замените распределенную нагрузку сосредоточенной и опре­делите расстояние от точки приложения равнодействующей до опо­ры А (рис. 6.9).

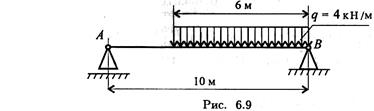
2. Рассчитайте величину суммарного момента сил системы от­носительно точки А (рис. 6.10).

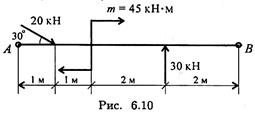
3. Какую из форм уравнений равновесия целесообразно исполь­зовать при определении реакций в заделке?

4. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?