Методы оценки надежности зданий с помощью математических моделей

Простейшая модель в предположении экспоненциальности

Рассматриваем n-мерный случайный процесс X(t)= x_x(t),...,x_n(t)с конечным множеством значений X и критическим множеством Q,попадание в которое интерпретируется как отказ всей системы. Считаются заданными следующие характеристики: α(х)-интенсивность выхода из состояния х; Р(у/х)-вероятность перехода из состояния х в состояние 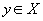,если выход из состояния х состоялся.

Пусть 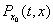-вероятность того, что за время t процесс не попал в критическое множество Q и в момент t он находится в точке х при условии, что в начальный момент процесс находился в точке х₀.

Обычными методами для функций мы получаем следующую систему дифференциальных уравнений

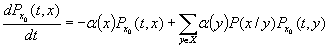(4.1)

для 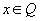и P_x(t,x) = Q. (4.2)

Начальные условия для системы 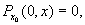если х ¹ x₀. Поскольку множество X конечно, система (4.2) имеет единственное решение и может быть решена, по крайней мере численно. Заметим, что число уравнений равно числу точек вне множества Q.

Функция надежности выражается через решение системы (4.2) с помощью соотношения 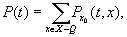где суммирование ведется по всем состояниям вне множества Q.

Полученная система кажется слишком сложной для практического использования. Чтобы убедиться, что это не так, рассмотрим численный пример.

Пример 2. Предположим, что система состоит из двух элементов и имеет три состояния с переходами и интенсивностями, изображенными на рис. 4.6.

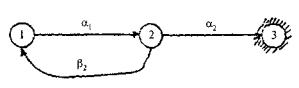
Рис. 4.6. Граф переходов из состояний для примера 2

При этом критическое множество состоит из одного состояния 3. В начальный момент система находится в состоянии 1. Нас интересует надежность системы, т.е. время до попадания в состояние 3. Система (4.1) принимает вид

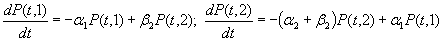(4.3)

с начальными условиями Р(0,1)=1, Р(0,2)=0. (Здесь для удобства опущен нижний индекс 1). Наиболее короткий метод решения системы (4.3) - использование преобразований Лапласа, т.е. функций вида

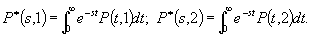
Для преобразований Лапласа вместо системы дифференциальных уравнений мы получаем систему алгебраических уравнений, интегрирование по частям дает

Итак, вместо (4.3) мы имеем

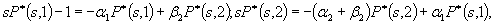(4.4)

откуда

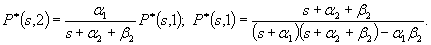(4.5)

Теперь необходимо обратить преобразование Лапласа для P(s,1). Обозначим s₁и s₂корни знаменателя в выражении (4.5) для P(s,1).Нетрудно проверить, что оба они отрицательны и

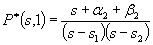
Значения s_1,2определяют из соотношения

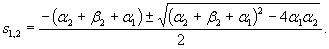
Для обращения преобразований Лапласа воспользуемся справочными данными и получим

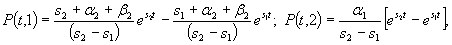
а надежность системы, т.е. вероятность того, что за время t не будет отказа

P(t) = P(t,1)+ P(t,2). (4.6)

На этом элементарном примере мы замечаем одно важное обстоятельство: функция надежности имеет экспоненциальный характер. Посмотрим, как ведет себя эта функция при большом t. Для определенности выберем s₂ < s₁,тогда при t → ¥

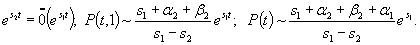(4.7)

В дальнейшем убедимся, что экспоненциальный характер функции надежности очень часто возникает в приложениях и объясняется целым рядом причин, коренящихся в характере случайных процессов, описывающих соответствующие объекты.

Пример 3. Рассмотрим с этих позиций пример, приведенный в § 4.2. Для простоты предположим, что грунт может находиться в двух состояниях: нормальное, без нарушения структуры, с несущей способностью, обеспечивающей нормальную эксплуатацию здания; нарушены физико-механические свойства, что может привести к неоднородным осадкам, просадкам фундамента и его разрушению.

Фундамент также может находиться в двух состояниях: нормальном, без видимых нарушений, с однородной допустимой осадкой; с потерянной несущей способностью вследствие разрушения полностью или части фундамента.

Вся система будет иметь четыре варианта состояний: 1 - нормальное состояние грунта и фундамента; 2 - нарушены физико-механические свойства грунта и несущая способность фундамента; 3 - нормальное состояние грунта, но фундамент разрушен и потерял несущую способность; 4 - нарушены физико-механические свойства грунта, и фундамент утратил несущую способность.

Критическое множество Q в этом случае содержит два состояния: (4.3) и (4.4). Граф переходов из состояния в состояние выглядит, как показано на рис. 4.7.

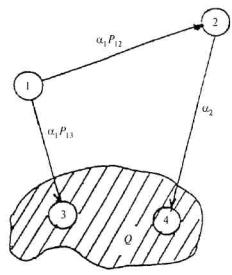
Рис. 4.7. Граф переходов
Состояния 3 и 4 образуют критическое множество

Пусть t₁-время, в течение которого в грунте не возникает опасных изменений; t₂ - время между возникновением опасных нарушений физико-механических свойств грунта и потерей несущей способности фундамента; 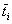- среднее значение t_i (i = 1,2).

Переход из состояния 1 в состояние 3 означает разрушение фундамента, не связанное с изменениями состояния грунтового основания.

Обозначим t₃-продолжительность нормального функционирования фундамента при условии, что грунт не подвергался никаким нарушениям.

В соответствии с развитой ранее техникой получим следующие значения для интенсивностей переходов

(4.8)

Система уравнений

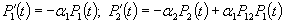
с начальными условиями Р₁(0)= 1, Р₂(0) = 0.

Решение:

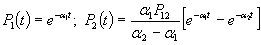
и вероятность отсутствия отказа до t

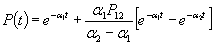(4.9)

Мы видим, что полученная зависимость (4.9) также носит экспоненциальный характер.

Небольшое усложнение модели позволяет учесть большое число состояний.

Основные трудности в применении предложенного метода состоят не в объеме вычислений, а в получении необходимых исходных данных.

Если имеется достаточное число наблюдений за поведением однотипных объектов, то величины, обратные интенсивности переходов, не что иное, как среднее время пребывания объекта в соответствующем состоянии.

Оценка среднего значения случайной величины по наблюдениям - это достаточно элементарная задача математической статистики.

Если объект уникален или нет достаточного числа наблюдений, математическая статистика помочь не может. Здесь можно использовать физико-механические методы.

Пусть, например, выход системы из данного состояния определяется значением некоторого числового параметра ξ(t) (осадка фундамента, степень уплотненности грунта, деформация конструкций и т.п.). Обычно ξ(t)-случайный процесс. Например, на конструкцию здания воздействуют следующие факторы: 1 - нагрузки (постоянные, временные, динамические, аварийные); 2 - окружающая среда (ветер, атмосферные осадки, солнечная радиация, неравномерные осадки оснований, землетрясения); 3 - внутренние источники напряжений (температура, усадки, ползучесть, перераспределение нагрузок).

Наличие большого числа факторов свидетельствует о том, что ξ(t) гауссовский процесс. Выход системы из состояния возникает тогда, когда значение характеристики ξ(t)превышает некоторый заданный уровень (например, нагрузка на несущие конструкции становится больше допустимой). Тогда нам нужно найти среднее время, за которое процесс ξ(t), выйдя из точки т, впервые пересечет уровень R. Эта задача имеет решение для целого ряда процессов.