Основная математическая модель для изучения надежности зданий

До сих пор мы говорили о понятиях надежности в самом общем плане. Однако если мы попытаемся ввести количественные показатели, то неизбежно приходим к вероятностной трактовке этих понятий.

Обычно под надежностью понимается вероятность безотказной работы в течение заданного промежутка времени. Наряду с этим встречаются и другие толкования этого термина. Вообще говоря, количественных характеристик надежности много, в каждом конкретном случае решающую роль могут играть различные показатели надежности.

В отличие от простых систем, где имеются только два возможных состояния - нормальное эксплуатационное и отказ, в зданиях большая часть конструкций и элементов может иметь несколько состояний, соответствующих частичным отказам и неисправностям. В связи с этим иногда- отказы классифицируют: частичный отказ узла или элемента, восстановление или усиление которого приводит к полному восстановлению надежности сооружений; отказ наиболее ответственных элементов сооружений (основания, фундаментов, колонн, ригелей и т.п.), приводящий к полному отказу всего сооружения. Отказы второй группы могут быть внезапными, а усиление этих элементов порой связано с большими объемами работ и экономическими затратами.

Таким образом, характеристики отказов должны отображать различные категории несущей способности здания или его частей. Предельно допустимую вероятность отказа, о которой мы еще будем говорить далее, следует определить в зависимости от тяжести последствий, как это всегда и делается в теории принятия решений. Обычно более надежным является изделие, работающее в мягких (благополучных) условиях эксплуатации, чем в жестких (предельных). Поэтому одним из способов повышения надежности, например в станкостроении, радиоэлектронике и т.п., является создание облегченных условий для работы изделий.

Специфика здания как изделия состоит: в невозможности создания облегченных условий для работы здания в целом, хотя для отдельных узлов и элементов такая возможность имеется; в трудности (или невозможности для некоторых элементов) использования резервирования.

Современные методы расчетов узлов и конструкций зданий (в частности, метод предельных состояний) сосредоточивают внимание на границах качества, хотя для многих характеристик (тепло-, звукоизоляция и др.) важно не только предельное состояние, но и распределение качества. Статистика показывает, что большая часть отказов и аварий происходит из-за так называемых мелочей: невыполнения всех поверочных расчетов конструкций, особенно при проектировании и при работе нескольких авторов, неаккуратности рабочих при изготовлении изделий и монтаже, отклонений от технологических режимов, неподготовленности обслуживающего эксплуатационного персонала и т.п.

Основной недостаток расчетов конструкций по предельным состояниям в том, что отсутствует фактор времени. Статистическую изменчивость нагрузок и механических свойств материалов конструкций указывают соответствующими коэффициентами запаса.

К сожалению, зависимость свойств материалов от времени невозможно прогнозировать с достаточной точностью на длительный промежуток времени. Разумеется, есть параметры, характеризующие свойства материалов, для которых тем или другим статистическим методом удается найти явные временные зависимости. Тем не менее следует отдавать отчет, что все эти параметры являются на самом деле случайными процессами и в лучшем случае мы получаем с помощью статистических исследований среднее их значение. Между тем надежность системы самым существенным образом зависит от статистических свойств этих случайных процессов.

В связи с этим предлагается достаточно общая математическая модель для оценки надежности сложной системы, работоспособность которой будет проиллюстрирована при оценке надежности реконструированных зданий.

Первый шаг состоит в разбиении сложной системы на ее составляющие - элементы. Способ разбиения определяется задачами, которые ставит перед собой исследователь, а также совокупностью статистического материала, которым он располагает.

В качестве примера рассмотрим здание, подлежащее реконструкции. На первом этапе исследования можно выделить следующие основные элементы: грунтовое основание; фундаментная часть; перекрытия; несущие стены продольные и поперечные; кровля.

Для описания состояния здания в каждый момент времени мы рассматриваем многомерный процесс X(t)= (x₁(t), ..., X_n(t)),n,так что в момент t состояние процесса описывается n-мерным (в нашем примере пятимерным) вектором. Каждая из компонент вектора X(t)может, в свою очередь, находиться в различных состояниях, так что компоненты принимают различные значения. Для практических расчетов достаточно предположить, что число этих значений конечно. Пусть е_i1,..., e_ik - возможные значения i-й компоненты.

Совокупность всех значений процесса X(t)принято называть фазовым пространством. Обозначим его X. В нашем случае X представляет собой конечное множество, состоящее из К₁´ К₂, ...,К_п точек. Если X(t)в момент t находится в точке (е₁,_j1, е₂,_j2, ..., е_п,_jn),это означает, что его первая координата принимает значение е₁,_j1, вторая е₂,_j2 и т.д. С позиции теории надежности в фазовом пространстве X выделяется некоторое подмножество состояний Q,попадание в которое процесса X(t)означает аварию (отказ). Тогда надежность системы Р(Т)за время Т есть вероятность того, что процесс X(t)за время Т,выйдя из некоторой фиксированной точки, не попадет во множество Q,т.е. .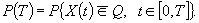

Чтобы сделать это понятие содержательным, необходимо задать вероятностно-статистические характеристики процесса X{t). Это второй шаг построения математической модели.

Мы будем строить это описание исходя из следующих предположений, которые в плане будущих применений к оценке надежности реконструированных зданий представляются достаточно естественными:

за малое время ∆t возможно изменение лишь одной из координат процесса;

за малое время ∆t возможен переход только в соседнее состояние.

Это означает, что возможные значения координаты перенумерованы таким образом, что возможны только переходы типа i → i + 1. Позднее мы проиллюстрируем это обстоятельство на примере.

Пусть теперь α_i,(x)∆t -вероятность того, что система за время ∆t из состояния х(х₁,..., х_n)перейдет в состояние 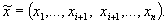.Если предположить, что переходы из одного состояния в другое зависят только от текущего состояния процесса, то совокупность функций {α_i(x), i = 1,2,...,п}полностью определяет вероятностные свойства процесса и, таким образом, математическая задача поставлена.

При этом возникают две основные проблемы:

- как на основании экспериментальных данных получить функцию α_i(x);

- как найти вероятность Р(Т),если α_i(x) ( i = 1,...,п)дана.

Первая проблема - из области математической статистики, но она самым тесным образом связана с предметной стороной исследования. Вторая проблема - очень трудная математическая задача, решенная к настоящему времени лишь для некоторых частных случаев.

Тем не менее есть математические идеи, позволяющие получить приближенное значение Р(Т). Они базируются на ряде математических теорем [95], утверждающих, что время достижения критического множества Q в достаточно общих предположениях, выполненных для широкого класса практических задач, имеет экспоненциальное распределение, так что 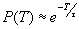, где τ - среднее время достижения критического уровня.

Проблема отыскания среднего времени τ достижения несравненно проще отыскания распределения. Более того, она может быть получена по результатам прошлых наблюдений за идентичными объектами.

Прежде чем переходить к моделям, связанным с надежностью зданий при их реконструкции, поясним сказанное на простом примере.

Пример 1. Рассмотрим систему, состоящую из двух элементов (например, элемент 1 - грунтовое основание здания, а элемент 2 - его фундаментная часть), так что фазовое пространство Xявляется двумерным с точками (х₁, х₂).

Зададим различные состояния грунтов, т.е. первой координаты, следующим образом:

состояние 1 - уплотненные фунты с допустимой осадкой и равномерной осадкой здания;

состояние 2 - грунты с нарушением их физико-механических свойств, однако не вызывающим опасения неравномерных осадок здания;

состояние 3 - грунты с таким нарушением их свойств, которое вызывает опасения относительно целостности здания;

состояние 4 - грунты с таким нарушением свойств, которое обычно вызывает неравномерную осадку здания и приводит к частичному разрушению фундамента;

состояние 5 - грунты с нарушением физико-механических свойств, обычно приводящим к полной потере несущей способности фундамента.

Итак, первая координата имеет 5 возможных состояний. При этом если не производятся работы, направленные на упрочнение и укрепление оснований, такие как поверхностное и глубинное уплотнение и инъецирование, закрепление силикатизацией, цементацией и другими техническими приемами, движение процесса по первой координате возможно только в одном направлении, т.е. схематически мы можем иметь только траекторию, представленную на рис. 4.4. Если, например, при достижении состояния 3 проводятся работы по упрочнению и укреплению основания, то возможен переход из состояния 3 в 2 или 1.

Рис. 4.4. Траектория процессов для примера 1

Мы предполагаем, что время выполнения работ по укреплению грунтов весьма мало по сравнению со временем функционирования системы и даже по сравнению со средним временем движения системы из одного состояния в другое. Это позволяет не вводить дополнительную переменную в наш случайный процесс X(t),которая фиксировала бы, на какой стадии находятся реконструктивные работы в данный момент. Итак, реконструктивные работы могут быть заданы такими вероятностями: 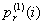- вероятность осуществления восстановительных работ, если первая координата находится в состоянии i; -вероятность перехода первой координаты из состояния i в состояние j £ i,если осуществляются восстановительные работы.

Переходим к определению возможных значений второй координаты (фундаменты) по состояниям: 1 - нормальное без видимых нарушений; 2 - локальные нарушения сцепления с кладочным раствором; 3 - повсеместное нарушение сцепления с кладочным раствором; 4 - сквозные трещины; 5 - потеря несущей способности (разрушение).

Итак, вторая координата нашего процесса также имеет пять возможных значений, и если не производятся работы по усилению, восстановлению или защите фундаментов от агрессивных воздействий, движение второй координаты возможно только в одном направлении, т.е. из состояния i в состояние i + 1. Учет восстановительных работ можно проводить так же, как для координаты х,вводя соответствующие вероятност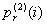и и .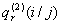

Критическое множество фазового пространства состоит из точек вида (i, 5), т.е. содержит все точки, в которых фундамент потерял несущую способность: Q = {( i,5), i = 1,2,3,4,5}.

Фазовое пространство X(t)состоит из 25 точек. Критическое множество содержит 5 точек.

На рис. 4.5 изображена одна из возможных траекторий процессов.

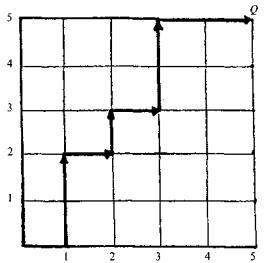
Рис. 4.5. Пример траектории процессов

Эта траектория соответствует такой ситуации: из нормального состояния грунта и фундамента (1,1) осуществляется переход в состояние, когда в грунте возникают первичные нарушения физико-механических свойств (состояние (2,1)), что приводит к локальным нарушениям сцепления с кладочным раствором в фундаменте (состояние (2,2)), далее в грунте происходят более глубокие нарушения физико-механических свойств (состояние (3,2)), что приводит к повсеместным нарушениям сцепления с кладочным раствором фундамента (состояние (3,3)) и т.д.

Математическая модель будет полностью определена, если будут заданы вероятностные характеристики, описывающие случайный процесс X(t). Наиболее простая модель получается при предположении экспоненциальности.

Времена пребывания случайного процесса X(t)в состоянии (i_l,i₂),коль скоро он туда попал, имеют экспоненциальное распределение с параметром a(i_l,i₂), по истечении этого времени процесс с вероятностью р(j_l,j₂/i_l,i₂) переходит в состояние (j_l,j₂).

Математически это предположение означает, что процесс X(t)является цепью Маркова с конечным множеством состояний и поглощающим множеством состояний Q. Задача вероятности поглощения за определенное время, т.е. по существу надежности системы, может быть решена достаточно стандартными приемами, по крайней мере численно.

Физически предположение об экспоненциальности означает, что мы рассматриваем только так называемые внезапные отказы, не связанные со старением здания, а вызванные скорее нежелательными флуктуациями внешней среды. Безусловно, такие отказы могут иметь место при эксплуатации зданий, но с точки зрения надежности реконструируемых зданий наибольший интерес представляют так называемые постепенные отказы, связанные с изменением свойств материалов при длительной эксплуатации, постепенной неравномерной осадкой здания, разрушениями кирпичной кладки, потерей несущей способности перекрытия из-за коррозии опорных частей, балок и т.п.

Некоторые исследователи считают, что распределение времени пребывания в любом состоянии близко к нормальному. Тем не менее этот вопрос требует глубокого анализа, который выходит за рамки данной работы, кроме того, в дальнейшем мы укажем приемы для оценки надежности реконструированных зданий, позволяющие обойти предположение об экспоненциальности.

Одним из таких приемов служит предположение о том, что интенсивности изменения состояния системы a(t, x)являются функциями не только состояния, но и времени. Это в значительной мере позволяет учесть старение материалов и конструкций, и такая модель хорошо описывает поведение системы в промежутках между ремонтами, возвращающими систему в начальное нормальное или близкое к нему состояние.