Расчет зубчатого зацепления на контактную прочность

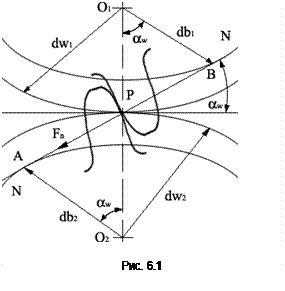
Расчет сводится к удовлетворению усло­вия, по которому контактные напряжения зубьев не должны превышать допускаемые. Расчет ведут для зацепления в полюсе (рис. 6.1), т.к. выкрашивание начинается у полюсной линии.

В качестве исходной принимают формулу Герца-Беляева для наибольших контактных напряжений при скольжении цилиндров, соприкасающихся вдоль образующей

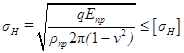. (6.1)

Входящие в формулу (6.1) величины известны из предыдущих лекций.

Обозначим 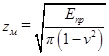- коэффициент, учитывающий механические свойства материала колес. Для стальных колес z_м=275 МПа.

Получим 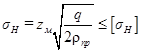. (6.2)

Здесь 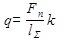- погонная нагрузка, где 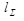- длина контактных линий

(в прямозубых передачах );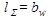

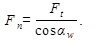
Так как 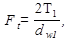получаем 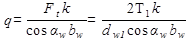. (6.3)

Приведенный радиус кривизны 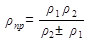. По свойству эвольвенты

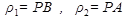, поэтому 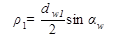и

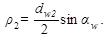
Так как 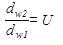, следовательно

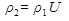и 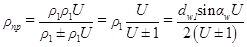. (6.4)

Подставив выражения (6.3) и (6.4) в уравнение (6.2), получим

.

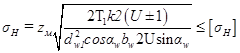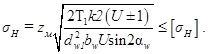Так как 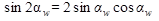, то

Обозначим 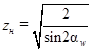- коэффициент, учитывающий форму сопряженных поверхностей ( при 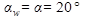коэффициент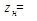 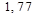), тогда

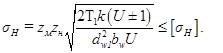В передачах высокой точности (выше седьмой) вводится коэффициент 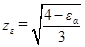, учитывающий влияние коэффициента торцевого перекрытия 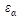. Этот коэффициент получен экспериментальным путем. При отсутствии необходимости повышенной точности расчета можно принимать 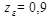, что соответствует .

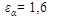Окончательно получим

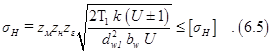Таким образом, контактная прочность зубчатых колес определяется межосевым расстоянием, передаточным числом и шириной зубчатого венца, но не зависит от модуля.