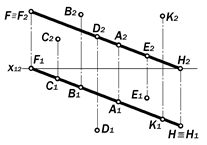
Графические модели проецирующих прямых и их изобразительные свойства

Геометрические модели прямых линий в системе двух плоскостей проекций

Прямыми линиями являются те, ко-торые сливаются, проходя через две несовпадающие точки. Они бесконечны и в проективном смысле замкнуты (см.

определение 6.12). Поэтому изобра-зить всю прямую невозможно. Обычно изображают участок прямой линии а между двумя её нетождественными точками А и В, называемый отрезком АВпрямой а.

По отношению к плоскостям проек-ций П₁ и П₂ прямые линии могут зани-

мать частные, т.е., параллельные и перпендикулярные к ним, и общее,т.е.,

не параллельные и не перпендикуляр-ные к ним, положения.

Определение 9.1.Прямые, парал-лельные плоскостям проекций или принадлежащие им, называются л и –

н и я м и у р о в н я: ( рис. 9.1)

b ^ П₂ - фронтально -проецирующая

прямая;

с^ П₃ – профильно-проецирующая

прямая.

Если прямые перпендикулярны к од-ной плоскости, то они параллельны другой или могут совпадать с ней. Это значит, что проецирующие прямые

занимают в пространстве д в а ж д ы ч а с т н о е положение и обладают всеми свойствами линий уровня.

Определение 9.3.Прямые, рас-положенные в пространстве произ-вольно, называются п р я м ы м и о б -щ е г о п о л о ж е н и я.

Следы прямых

Если прямые не параллельны пло-скостям проекций, то они с ними пере-секаются.

Определение 9.4.Точки пересе-чения изображаемых прямых с плоско-стями проекций называются с л е д а- м и прямых (см. п.5.1,определение 2.10).

Следы прямых бывают горизонта-льными,фронтальными и профильны-ми, в зависимости от того, с какими плоскостями проекций эти прямые пе-ресекаются. Основным позиционным свойством следов прямых линий яв-ляется их двойная природа, ибо они одновременно принадлежат и плоско-сти проекций и самой прямой, т.е., сами себя изображают. Отсюда следует, что построение следа прямой равносильно построению соответствующей проекции одной её точки.

Совершенно очевидно, что в си-стеме двух плоскостей проекций линии уровня и проецирующие прямые имеют по одному следу, а прямые общего положения, – по два.

9.2.Графические модели линий уровня и их изобразительные свойства(рис.9.4 – 9.6)

Так как прямая линия задаётся дву-мя нетождественными точками, то для её изображения достаточно изобразить эти точки и соединить их одноименные проекции под линейку.

Рис.9.4. Графические модели горизонтальных прямых

Рис.9.5. Графические модели фронтальных прямых

Рис.9.6. Графическая модель профильной прямой

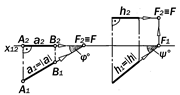
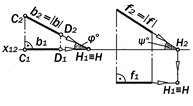
Рис. 9.7.Графические модели проеци-рующих прямых

Рис.9.8. Графическая модель прямой общего положения

Одной из таких точек может быть след линии уровня, а если прямая об-щего положения, то обе точки могут быть её разноименными следами.

Для построения следов прямых ли-ний необходимо графически промоде-лировать два их позиционных свой-ства:

1. принадлежность следа к изобра-жаемой прямой и

2. принадлежность следа к плоскос-ти проекций.

Так как след принадлежит плоскости проекций, то одна из его проекций обя-зательно принадлежит оси проекций. Эта первая проекция следа строится как точка пересечения с осью той про-екции прямой, которая ей не парал-лельна. Вторая проекция следа строит-ся в проекционной связи с первой на второй проекции прямой, которая мо-жет быть параллельной или не парал-лельной оси проекций (см. рис.9.1- 9.5).

Изобразительные свойства проекций линий уровня

Позиционные свойства:

(в осной системе) (в безосной системе)

1. аÎП₁ Þа₂Îх₁₂ ; ¾

2. bÎП₂ Þ b₁Îх₁₂; ¾

3. h || П₁Þ h ₂ || x₁₂; h || П₁ Þ h₂^A₂A₁;

4. f || П₂ Þ f₁ || x₁₂; f || П₂ Þ f₁^ A₂A₁;

5. p || П₃Þ(р₁ºА₂А₁ p || П₃ Þр₁º

ºр₂)^х₁₂ ; º А₂А₁º р_2..

Утверждение 9.1. Горизонталь-ность одной из проекций прямой линии является графическим признаком то-го, что изображенная прямая являет-ся линией уровня.

Метрические свойства проекций

прямых линий

Метрическими характеристиками прямой линии является натуральная величина расстояния между двумя её точками и натуральные величины углов её наклона к плоскостям проек-ций.

Так как линии уровня параллельны плоскостям проекций, то они проециру-ются на них в свою натуральную ве-личину. По этой же причине угол на-клона прямой к той плоскости проекций,

по отношению к которой она не парал-лельна, проецируется в натуральную величину на ту плоскость проекций, по отношению к которой она параллельна:

1. h || П₁ Þ h₁ = | h |;

2. f || П₂ Þ f ₂ = | f |;

3. c ^П₁ Þ с || П₂ Ù с₂ = | c |;

4. d ^П₂ Þ d || П₁ Ù d₁ = | d |;

5. p || П₃ Þ р₃ = | p |;

6. h || П₁ Þ h₁ ^ x₁₂ = j° = | h ^ П₂ | ;

7. f || П₂ Þ f₂ ^ x₁₂ = y° = | f ^ П₁ | ;

8.c^П₁ Þ с ^ П₁ = 90° ;

9.d^П₂ Þ d ^ П₂ = 90° ;

10. р || П₃ Þ р₃ ^ z₂₃ = j° = | p ^ П₂ | Ù

Ù p₃ ^ y₃ = y° = | p ^ П₁ | .

Графические модели проецирующих прямых и их изобразительные свойства

(рис. 9.7)

Так как проецирующие прямые за-нимают дважды частное положение, то их невырожденные проекции равны их натуральным величинам, а вырожден-ные в точку обладают с о б и р а т е -л ь н ы м свойством (см.п. 5.1, опреде-ление 2.7).

1. с ^ П₁ Þ с₂ = | c |, c₁ – точка;

2. d ^ П₃ Þ d₁ = | d |, d ₂ – точка;

3. q ^ П₃ Þ q₁, q₂ = | q |, q₃ –точка.

Утверждение 9.2.Точка, как вы-рожденная проекция прямой, являет-ся графическим признаком того, что изображенная прямая является прое-цирующей.

Утверждение9.3.(общее). Орто-

гональные проекции прямых линии ча-стного положения содержат в себе не-посредственную информацию об их по-зиционных и метрических свойствах.

9.4.Графические модели прямых общего положения и их изобра-зительные свойства

(рис. 9.8, 9.9)

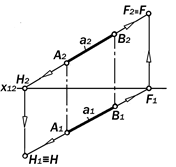
Если обе проекции прямой явля-ются прямыми, не параллельными и не перпендикулярными к осям проекций или вертикальным линиям связи, то изображенная ими прямая занимает в пространстве общее положение ( рис. 9.8).

 

 

Рис9.9. Геометрическая модель идеи способа прямоугольного треугольник

 

 

Рис.9.10. Правило прямоугольного

треугольника

 

 

Если отрезок прямой не параллелен плоскости проекций, то длина его орто-

гональной проекции на эту плоскость не равна длине самого отрезка, а мень-ше неё на косинус угла его наклона к этой плоскости.

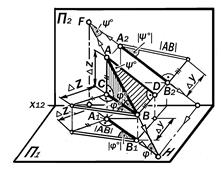
Из рис 9.9. видно, что отрезок АВ является ребром некоторого тетраэдра АВСD, по которому пересекаются две его грани в виде прямоугольных тре-угольников АВС и АВD, катеты ВС и АD которых являются соответственно гори-зонтальной и фронтальной линиями уровня, метрически равными горизонта-льной и фронтальной проекциям отрез-ка АВ.

Углы между гипотенузой АВ и прилежащими катетами ВС и АD метрически равны натуральным величинам углов

наклона отрезка АВ к П₂ и П_1, а длина гипотенузы АВ этих треугольников равна длине отрезка АВ общего положе-ния. Для графического по-строения гипотенузы пря-моугольного треугольника не-обходимо иметь два его кате-та. Информация о этих катетах непо-средственно присутствует на комплек-сном чертеже. Ведь прилежащий к углу наклона катет равен данной проекции отрезка, а противолежащий равен раз-ности расстояний другой его проекции до оси проекций.

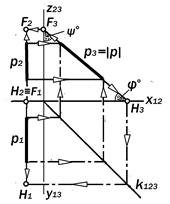
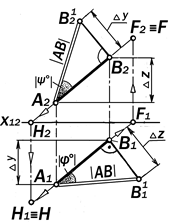
Отсюда вытекает правило прямо-угольного треугольника для опреде-ления длины отрезка прямой общего положения и величин углов его наклона к плоскостям проекций по его ортого-нальному комплексному чертежу (рис. 11.9):

Натуральной величиной отрезка

прямой общего положения является длина гипотенузы прямоугольного треугольника, одним из катетов ко-торого является одна из проекций этого отрезка, а второй катет ме-трически равен разности расстояний концов другой его проекции до оси про-екций.

Натуральной величиной угла j° на-клона отрезка АВ к плоскости П₁ явля-ется значение угла между горизонталь-ной проекцией отрезка и его натураль-ной величиной.

Натуральной величиной угла y° на-

клона отрезка АВ к плоскости П₂ явля-

ется значение угла между фронтальной проекцией отрезка и его натуральной величиной.

Утверждение 9.4.Ортогональ-ные проекции отрезка прямой обще-го положения не содержат в себе не-посредственной информации о его метрике, но содержат все необходи-мые данные для её определения.

 

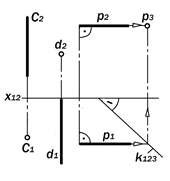
9.5.Графические модели простейших двухэлементных систем из точек и прямых и их изобразительные свойства

Двавозможных варианта систем из точек и одной прямой

1. А, В, С,…Î а; 2.А,В,С,…Ï а.

Рис.9.11. Геометрическая модель

системы из точек и прямой

Точка, не принадлежащая прямой, может быть над, под, перед, за, правее, правее и выше (ниже, дальше, ближе) и левее (ниже, дальше, ближе) этой пря-мой.

Утверждение 9.5.Если точка принадлежит прямой, то одноимен-ные проекции этой точки и этой пря-мой инцидентны (рис. 9.12)

А Î а Þ А₁ Î а₁ , А₂ Î а₂ .

 

Рис.9.12.Графическая модель системы из точек и прямой

Утверждение 9.6.Если точка не при-

надлежит прямой, то одна или обе её проекции не принадлежат соответст-вующим проекциям этой прямой (рис. 9.12).

Рис.9.13. Геометрические модели

систем из двух прямых

 

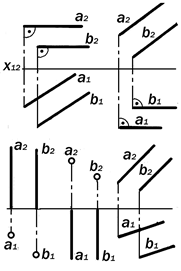
Рис. 9.14. Графические модели двух параллельных прямых

 

Рис. 9.15.Графические модели двух пересекающихся прямых

 

А Ï а Þ А₁ Ï а₁ , А ₂ Ï а ₂ ;

А Ï а Þ А₁ Î а₁ , А ₂ Ï а _{2 ;}

А Ï а Þ А₁ Ï а₁ , А ₂ Î а _2.

 

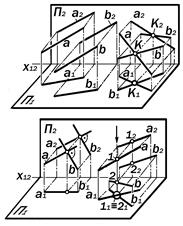
9.6. Геометрические модели систем из двух прямых(рис. 9.13)

1. а || b; 2. с ´ d = K;

3. a ^ b;4. a @ b.

 

Относителтьно друг друга прямые мо-гут быть параллельными, пересекаю-щимися, в том числе, и под прямым уг-лом, и скрещивающимися.

Относительно плоскостей проекций прямые этих систем могут занимать как частные, так и общее положение.

 

1.Параллельные прямые ( рис.9.14):

 

1.1. ( a || П₁ ) || ( b || П₁ );

1.2. ( a || П₂ ) || ( b || П₂);

1.3. ( a ∦ П₁; П₂ ) || ( b ∦ П₁; П₂ ).

 

Утверждение 9.7.Если две прямые в пространстве параллельны, то их одноименные проекции параллельны.

a || b Þ a₁ || b₁ , a₂ || b ₂ .

 

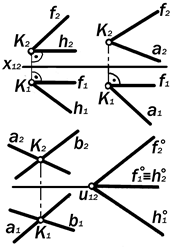
2.Пересекающиеся прямые (рис 9.15):

 

2.1. ( h || П₁ ) х ( f || П₂ ) = K;

2.2. ( a ∦ П₁) x ( f || П₂ ) = K;

2.3. ( a ∦ П₁, П₂ ) x ( b ∦ П₁, П₂) = K.

2.4. ( h Î П₁ ) x ( f Î П₂ ) = u_12.

 

Утверждение 9.8. Если прямые в пространстве пересекаются, то их одноименные проекции также пересе-каются, а разноименные проекции то-чки их пересечения лежат на одной вертикальной линии связи.

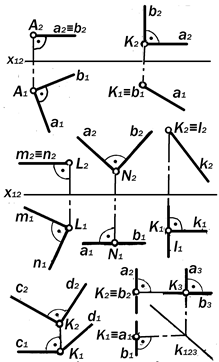
3. Перпендикулярные прямые

(рис. 9.16)

3.1. ( а || П₁ ) ^ ( b || П₁ ) = А ;

3.2. ( a ⊥ П₁ ) ^ ( b ^ П₁ ) = K ;

3.3. ( m || П₁) ^ ( n || П₁) = L ;

3.4. ( a || П₂ ) ^ ( b || П₂ ) = N ;

3.5. ( l || П₂ ) ^ ( k || П₁) = K ;

3.6. ( c || П₂ ) ^ ( d ∦ П₂ ) = K ;

3.7. (a ^ П₁ ) ^ ( b ^ П₂ ) = K ;

Рис.9.16. Графические модели взаимно-перпендикулярных прямых

 

Геометрическая модель системы из двух взаимно-перпендикулярных пря-мых предполагает такие 7 вариантов их расположения в пространстве, когда прямой угол между ними проецируется в прямой угол между их проекциями (рис.9.16).

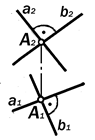
Утверждение 9.9.Прямой угол проецируется в натуральную величи-ну на ту плоскость проекций, по отно-шению к которой либо обе его сторо-ны, либо одна из них параллельна.

Изобразительной особенностью комплексного чертежа прямого линей-ного угла является наличие на нем двух прямых углов. Один между одной из проекций его стороны -- линии уровня и вертикальной линией связи, второй, – собственно изображаемый угол.

8-й вариант расположения

сторон прямо-

го угла пред-

полагает их

общее поло-

жение. В этом

случае пря-

мой угол бу-

Рис. 9.17.Угол междудет проециро-

прямыми а и b непрямой ваться в ту- или острый, но не в прямой (рис. 9.17).

Рис. 9.18. Графические модели двух

скрещивающихся прямых

 

 

Рис. 9.19.Геометрическая модель горизонтально-проецирующей плоскости

Отсюда следует утверждение 9.10:

Если между одноименными проекциями двух пересекающихся прямых прямые углы, то изображенный угол между этими прямыми в пространстве не яв-ляется прямым.

Задача на построение проекций прямого угла со сторонами общего по-ложения является позиционной, тре-бующей выполнения последовательных графических операций, и поэтому будет рассмотрена выше (см. рис.10.35) .

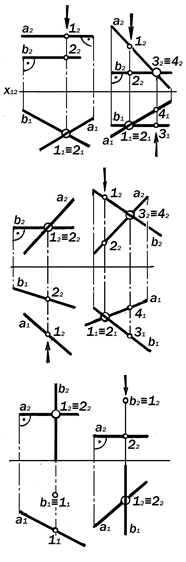
4.Скрещивающиеся прямые (рис.9.18).

 

Для того, чтобы прямые в прост-ранстве скрещивались, необходимо на-рушить в их расположении условия параллельности и пересечения.

4.1. ( a || П₁ ) ∸ ( b || П₁ );

4.2. ( a⊥П₃ ) ∸ ( b ∦П₁, ∦П₂ );

4.3. ( a – о.п.) ∸ ( b || П₁);

4.4. ( a – о.п.) ∸ ( b – о.п. );

4.5. ( a || П₁ ) ∸ ( b ⊥ П₁);

4.6. ( a || П₁) ∸ ( b ⊥П₂ ).

Это означает, что на их комплекс-ных чертежах должны отсутствовать графические признаки таких располо-жений. (см. утверждения 9. 7 и 9. 8).

 

Утверждение 9.11.Если прямыев пространстве скрещиваются, то их одноименные проекции в общем случае пересекаются, но разноименные про-екции точек их пересечения не лежат на одной вертикальной линии связи.

Возникает вопрос: что изображаютточки пересечения одноименных проек-ций двух скрещивающихся прямых?

Ответ: Они изображают такие две точки на этих прямых, которые лежат на одном проецирующем луче.

 

Определение 9.4.Точки двух скре-

щивающихся прямых, лежащие на од-ном проецирующем луче, называются к о н к у р и р у ю щ и м и.

На основе анализа взаимного рас-положения конкурирующих точек двух скрещивающихся прямых определяют

видимость этих прямых в составе не-

сквозных пространственных систем.

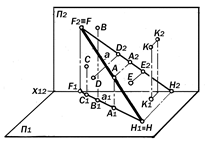
Пример 9.1.: Определить проекции не-видимых рёбер тетраэдра ( рис.9.20 ).

 

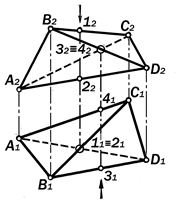
Рис.9.20. Анализ положения конкурирующих точек

 

Анализ условия: На горизонтальной проекции тетраэдра пересекаются проек-ции скрещивающихся рёбер АD и ВС в точке, где 1₁ º 2₁;

На фронтальной проекции тетраэдра пересекаются проекции скрещивающихся прямых АС и ВD в точке, где 3₂ º 4₂ .

Решение: 1. Определив фронтальные проекции 1₂ и 2₂ конкурирующих точек 1 и 2 на рёбрах ВС и АD, видим, что точка 1 на ребре ВС дальше от П₁, чем точка 2 на ребре АС и поэтому на виде сверху про-екция В₁С₁ будет видимой, а проекция

А₁D₁ - невидимой.

2. Определив горизонтальные проек-ции 3₁ и 4₁ конкурирующих точек 3 и 4 на рёбрах АС и ВD, видим, что точка 3 на ре-бре АС дальше от П₂ , чем точка 4 на ребре АС и поэтому на виде спереди проекция А₂D_2, будет видимой, а проекция А₂С₂ - невидимой.

 

Утверждение 9.12.На комплек-сном чертеже непрозрачного гранного объекта видимыми будут те проекции его скрещивающихся рёбер, конкуриру-ющие точки которых расположены в пространстве дальше от соответст-вующих плоскостей проекций.

Это происходит потому, что, распо-лагаясь по направлениям проециро-вания дальше от плоскостейпроекций, они закрывают собой те конкурирующие точки, которые ближек этим плоскос-тям и поэтому невидимы. Определение видимости проекций элементов на чер-тежах пространственных систем обяза-тельно.

 

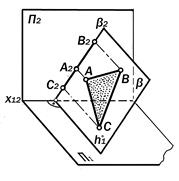
Рис. 9.21. Геометрическая модель фронтально-проецирующей плоскости

 

 

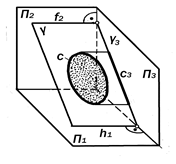
Рис.9.22. Геометрическая модель профильно-проецирующей плоскости

 

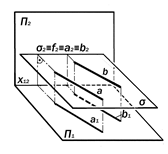
Рис.9.23. Геометрическая модель горизонтальной плоскости уровня

 

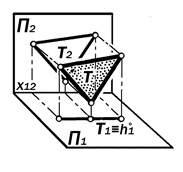
Рис.9.24. Геометрическая модель фронтальной плоскости уровня

9.7. Геометрия ортогональных проекций плоскости

Общие положения

Плоскость является системой ком-планарных точек и линий. Она задаётся этими её элементами и простирается в двух взаимно-перпендикулярных напра-влениях до бесконечности. Эвклидова плоскость бесконечна и безгранична и поэтому всю её изобразить невозмож--но.

Проективная плоскость (см. глава 2, определение 2.14) также бесконечна, но концептуально гранична, ибо она замкнута по бесконечно-удалённой прямой, которая, в частности, у любой горизонтальной плоскости зрительно воспринимается как линия горизонта или граница, на которой «земля схо-дится с небом». Другими словами, про-ективная плоскость подобна сфере бес-конечно большого радиуса и поэтому всю её изобразить также невозможно.

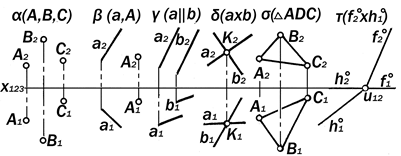
Практически плоскости изображают-ся элементами их определителей, т.е., следующими системами компланарных точек и линий:

1.a (А,В,С) - тремя неколлинейны-

ми точками;

2.b ( А, а ) - точкой и неинцидент-

ной ей прямой;

3. g ( а || b ) - двумя параллельны-

ми прямыми;

4.d ( a´b ) - двумя пересекающими-

ся прямыми;

5.s (DABC) - плоской фигурой;

6.t ( f₂°´h₁° ) - следами;

7. w ( O ) - плоской фигурой.

Все способы задания плоскостей геометрически равноценны, так как могут взаимно перезадаваться.

9.7.1. Геометрические модели плоскостей в системе двух плоскостей проекций

По отношению к плоскостям проек-ций П₁ и П₂ изображаемые плоскости могут занимать частные и общееполо-жение.

Частные положения плоскостей де-лятся на проецирующие и уровня.

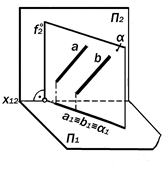
Определение 9.5Плоскости, пер-пендикулярные к плоскостям проек-

ций, называются п р о е ц и р у ю щ и-

м и ( рис. 9.19 – 9.22 ):

a^ П₁ – горизонтально-проеци-рующая плоскость;

b ^ П₂ – фронтально-проециру-ющая плоскость;

g ^ П₃ – профильно-проециру-ющая плоскость.

Определение 9.6.Плоскости, па-раллельные плоскостям проекций, на-зываются п л о с к о с т я м и у р о в-н я (рис. 9.23 – 9.25).

s || П₁ – горизонтальная плоскость

уровня;

t || П₂ – фронтальная плоскость

уровня;

w || П₃ – профильная плоскость уро-

вня.

Плоскости уровня занимают в про-странстве дважды частное положение, так как будучи параллельными к одной из плоскостей проекций, они перпен-дикулярны к другой и поэтому облада-ют всеми свойствами проецирующих плоскостей.

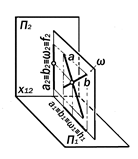
Рис.9.25.. Геометрическая модель про-

фильной плоскости уровня

Определение 9.7.Плоскости, расположенные в пространстве про-извольно, т.е., не параллельно и не перпендикулярно ни к одной плоско-сти проекций, называются п л о с к о- с т я м и о б щ е г о п о л о ж е н и я

(рис. 9.26.).

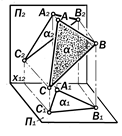
Рис. 9.26. Геометрическая модель

плоскости общего положения

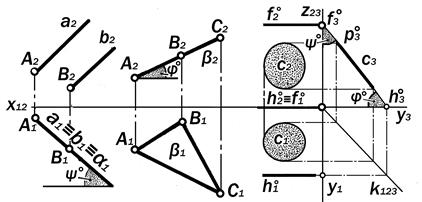
Рис.9.27.Графические модели

проецирующих плоскостей

9.7.2.Графические модели

плоскостей различного положения в пространстве и их изобразительные свойства

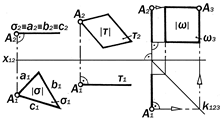
Графические модели проецирующих плоскостей и их изобразительные свойства(рис.9.27)

Если плоскость является проециру-ющей, то она проходит через центр про-ецирования и, будучи перпендикуляр-ной к соответствующей плоскости про-екций, проецирует себя на неё в пря-мую линию. Так как эта прямая изобра-жает в с ю плоскость с её инциденция-ми, то с ней совпадают или на ней соби-раются проекции всех точек и линий этой плоскости.

Определение 9.8.Способность вырожденной в прямую линию проек-ции проецирующей плоскости приво-дить в тождественное расположение соответствующие проекции компла-нарных точек и линий называется её

с о б и р а т е л ь н ы м свойством.

Утверждение 9.13.Прямолинейно-сть одной из проекций изображаемой плоскости является графическим при-знаком того, что эта плоскость прое-цирующая.

Метрические свойства проекций проецирующих плоскостей

Так как проецирующие плоскости не параллельны ни одной из плоскостей проекций, то проекции их плоских фигур не могут быть им конгруэнтны. Другими словами, на комплексном чертеже про-ецирующей плоскости нет непосред-ственной информации о натуральном виде её плоских фигур.

Так как проецирующие плоскости с

одной из плоскостей проекций состав-ляют прямой угол и поэтому проециру-ются на неё в прямую линию, то с этой прямой и осью проекций совпадут соответствующие проекции линейного угла как меры того двугранного угла, который составляется изображаемой плоскостью и той плоскостью проекций, к которой она не перпендикулярна.

Утверждение 9.14.Величина ли-нейного угла между вырожденной про-екцией изображенной плоскости и осью проекций метрически равна на-туральной величине угла наклона этой плоскости к той плоскости про-екций, к которой она не перпендику-лярна.

Отсюда следует, что комплексные чертежи проецирующих плоскостей содержат в себе непосредственную информацию о величинах двугранных

углов между ними и не перпендикуляр-

ными к ним плоскостями проекций.

Рис.9.28. Графические модели плоскостей

уровня

Графические модели плоскостей уровня и их изобразительные свойства ( рис.9.28)

Будучи проецирующей, плоскость уровня на одной плоскости проекций изображается в виде прямой линии, па-раллельной оси проекций (или пер-пендикулярной к вертикальной линии связи), а на второй – в поле точек, конгруэнтное её точечному полю.

s|| П₁ Þ s₂ ^ А ₂ А₁ , s₁ = |s | ;

t|| П₂ Þ t₁ ^ А₂ А₁ , t ₂ = | t | ;

w || П₃ Þ w₁, w₂ º А₂ А_1, w₃ = | w |.

Это значит, что её вырожденная проекция обладает собирательным

свойством, а невырожденная изобра-жает все её конструктивные элементы в натуральную величину.

Рис.9.29. Графические модели

плоскостей общего положения

Метрические свойствапроекций

плоскостей уровня

Особенности метрических свойств

проекций плоскостей уровня определя-

ются особенностями их позиционных

свойств.

Так как эти плоскости параллельны одним плоскостям проекций и перпен-дикулярны к другим, то с одними они составляют углы в 0°, а с другими - 90°,т.е.:

s || П₁ Þ Ð s, П₁ = 0° , Ð s, П ₂ = 90°;

t || П₂ Þ Ð t, П ₂ = 0° , Ð t, П₁ = 90°;

w || П₃ Þ Ðw,П ₃ = 0°, Ð w, П₁ Ù

Ù Ð w,П ₂ =90°.

Способность плоскостей уровня проецироваться на параллельные им плоскости проекций в натуральную ве-личину даёт возможность непосредст-венных измерений проекций для опре-деления метрических характеристик изображенных плоских фигур ( их раз-меры, углы и расстояния между их эле-ментами, а также их площади).

Утверждение 9.15.Комплексные чертежи плоскостей уровня содержат в себе непосредственную информацию о позиционных и метрических свойст-вах изображенных плоских фигур.