Графические модели плоскостей общего положения и их

Так как плоскости общего положе-ния не являются проецирующими, то ни одна из их проекций не является вы-рожденной в прямую линию и поэтому не обладают собирательным свойст-вом.

Так как плоскости общего положе-ния не являются плоскостями уровня,

то ни одна из проекций их плоских фи-

гур не конгруэнтна этим фигурам.

Отсюда следует, что комплексные

чертежи плоскостей общего положения не содержат непосредственной инфо-рмации о метрических характеристиках изображенных плоских фигур, опреде-ляющих их конкретное общее положе-ние.

Для определения этих характе-ристик необходимо графически решить соответствующие метрические задачи путем преобразования проекций фигу-ры общего положения в проекции этой же фигуры, но занимающей такое ча-стное положение, изображение кото-рого будет непосредственно содержать искомую метрическую информацию.

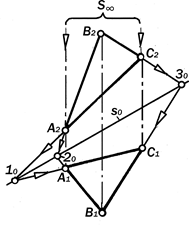
Рассматривая комплексный чертёж плоской фигуры, в частности, треуголь-ника АВС (рис. 9.30), обращаем вни-мание на то, что соответственные раз-ноименные проекции его вершин А, В и С лежат на параллельных, т.е., пересе-

Рис. 9.30. Двухкартинный комплексный чертеж плоской фигуры как дезаргова конфигурация

кающихся в бесконечно-удалённой точ-ке S_¥ линиях связи, а при продолжении его соответственных сторон убежда-емся, что они пересекаются в точках 1₀, 2₀, 3₀, лежащих на одной прямой s₀.

Отсюда следует вывод:Двухкар-тинный комплексный чертёж плоской фигуры является графической конс-трукцией, удовлетворяющей услови-ям теоремы Дезарга, а поэтому раз-ноименные проекции этой фигуры перспективно-аффинны или родст-

венны, т.е., являются гомологичными

фигурами.

Рис.9.31. Положительно равнонаклонённая плоскость

Рис.9.32. Отрицательно равнонаклонённая плоскость

Рис9.33. Графическая модель положительно равнонаклонённой плоскости

Рис.9.34. Графическая модель отрицательно равнонаклонённой плоскости

Рис.9.35. Изобразительные свойства отогональных проекций равнонаклонённых плоскостей

Другими словами, двукартинный комплексный чертёж плоской фигуры задаёт на картине гомологию, т.е.,даёт возможность по заданной проек-ции строить ей соответственную по гра-фическим законам теоремы Дезарга.

Двухкартинный комплексный чер-тёж треугольника АВС как графическая конструкция интересен тем, что эле-ментами его структуры являются 10 то-чек (S_¥, А₁, А₂, В₁ В₂, С₁, С₂, 1₀, 2₀, 3₀) и 10 прямых (А₁А₂, В₁В₂, С₁С₂, А₁В₁ А₂В₂, В₁С₁, В₂С₂, А₁ С₁ , А₂С₂, s₀), которые так взаимосвязаны отношениями инциден-тности, что через каждую точку прохо-дят по три прямые, а на каждой прямой лежит по три точки.

Такая закономерная графическая конструкция называется к о н ф и г у – р а ц и е й Д е з а р г а и она справедлива не только в плоскости, но и в пространстве.

9.7.3.Графические модели

равнонаклонённых плоскостей и их позиционные свойства

К числу позиционных особенностей не-которых плоскостей общего положения от-носится их равнонаклонённость к разным плоскостям проекций.

Определение 9.9. Плоскости общего положения, составляющие метрически равные углы наклона к разноименным пло-скостям проекций, называются равнона-клонёнными.

Конструктивно они могут быть двух ви-дов: положительно (рис.9.31) и отрица-тельно равно наклоненными (9.32).

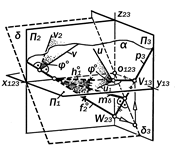
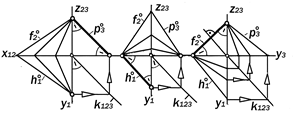
У первых одинаковые углы j° между линиями u и v наибольшего уклона к П₁ и П₂ и их проекциями на эти плоскости распо-ложены по одну от них сторону, а у вторых, - по разные стороны. Равнонаклонённость этих плоскостей к П₁ и П₂ определя-ет изобразительные свойства их зада- ния следами ( или линиями уровня) на 2-х и 3-х картинном комплексном черте- же (рис 9.33 -- 9. 35).

Утверждение 9.16.:Если плоскость a по- ложительно равнонаклонена к П₁ и к П₂, то её гори зональный h°₁ и фронталь-ный f°₂ следы равнонаклонённы к оси х_12, а профильный след р°₃ параллелен постоянной прямой k₁₂₃ трёхкартинного комплексного чертежа.

Из рис.9.31 видно, что треугольник сле-дов U₁₂ V₁₃ W₂₃ является равнобедренным. Его основанием служит профильный р°₃ след плоскости a, который параллелен профильному следу d°₃ биссекторной плос-кости d, откуда следует, что плоскость a пересекает эту биссекторную плоскость по её профильной линии уровня m_d , прохо-дящей через точку U₁₂ схода следов плос-кости a.

Утверждение 9.17.Если плоскость a отрицательно равнонаклонена к П₁ и к П₂, то её горизонтальный и фронтальный следы являются продолжением друг дру-га, а профильный след перпендикулярен к постоянной прямой k₁₂₃ трёхкартинного комплексного чертежа.

Из рис. 9.32 видно, что треугольник следов U₁₂ V₁₃ W₂₃ является равнобед-ренным, а линия пересечения плоскости a с биссекторной плоскостью d является биссектрисойострого угла между её гори-зонтальным и фронтальным следами.

Таким образом, равнобедренность тре-угольника следов плоскости a является графическим признаком её равнонакло-нённости к тем плоскостям проекций, с которыми она пересекается по его равным сторонам. При этом положение основания треугольника следов по отношению к пос-тоянной прямой k₁₂₃ говорит о характере равнонаклонённости ( положительная или отрицательная) и о плоскостях проекций, к которым она осуществляется ( рис.9.35 ):

1. p°₃ || k₁₂₃ Þ a^П₁ = a^П₂ ;

2. h°₁ || k₁₂₃ Þ a^П₂ = a^П_{3 ;}

3. f°₂ ^ k₁₂₃ Þ a^П₁ = a^П_{3 .}

Если равные между собой отрезки сле-

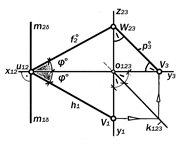
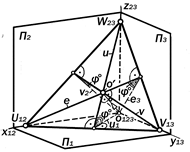
дов р°₃, h°₁ и f°₂ привести в состояние пе-ресекаемости на осях х₁₂, у₁₃ и z₂₃, то они образуют равносторонний треугольник сле-дов плоскости a, равнонаклонённый ктрём плоскостям проекций ( рис. 9.36).

Рис. 9.36. Плоскость, равнонаклонённая к трём плоскостям проекций.

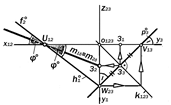
Рис 9.37..Графическая модель плоскости, равнонаклонённой к трём плоскостям проекций

Такая плоскость единственна. Её конст-руктивной особенностью является совпа-дение линий наибольших уклонов u, v, e к плоскостям проекций П₁, П₂ и П₃ с высота-ми, медианами и биссектрисами треуголь-ника следов, точкой О¢ пересечения кото-рых является основание перпендикуляра, опущенного из начала координат О₁₂₃ на плоскость a. Длина Н этого перпендикуляра определя- ет высоту пирамиды О₁₂₃ U₁₂ V₁₃ W₂₃ c равными рёбрами и прямыми углами при вершине О₁₂₃ ( рис. 9.37).

Изобразительной особеннос-

тью трёхкартинного комплексно-го чертежа такой плоскости яв-ляется взаимная перпендидику-лярность её следов ( h°₁^ f°₂^ p°₃ ), из которых h°₁ || p°₃ || k₁₂₃ , a f°₂ ^ k_123.

На рис 9.37 способом засе-чек по трём известным сторо-нам построен треугольник следов в его натуральную величину, а способом прямоугольного треугольника определено значение угла j° наклона плоскости a к плоскостям проекций П₁, П₂ и П₃, а также расстояние Н от точки О₁₂₃ до плоскости a.