Геометрия ортогональных

Проекций точек

8.2.1. Двухкартинный комплексный

чертеж точки

Геометрические модели точек пространства в системе 2-х

плоскостей проекций (рис.8.6)

Точки А, В, С, … в эвклидовом про-странстве могут отличаться только сво-им положением по отношению к плос-костям проекций П₁ и П₂, а также к d, т.е., они могут располагаться в разных его квадрантах, совпадать с плоскостя-ми проекций, с биссекторной плоскос-тью d, а также с осью х₁₂ .

С введением биссекторной плоско-сти d угла совмещения плоскостей П₁ и П₂ практически отпадает необходимо-сть в П₁.

Точки пространства, независимо от их положения в том или ином квадранте прежде из центра S¹_¥ проецируются, минуя П₁, на d, а затем полученные на ней проекции из центра S² проециру-ются на П¢ º П_{2 .} Тем самым устраняет-ся процесс совмещения П₁ с П₂ и свя-занное с ним искривление проецирую-щих лучей.

Графические модели различных точек пространства в системе 2-х плоскостей проекций (рис.8.7)

Определение 8.4.Графическая мо-дель точки в системе двух плоскос-

тей проекций называется б и н а р –

н о й.

Определение 8.5.Всякая пара кол-линейных разноименных проекций то-чки на вертикальной линии связи явля-ется бинарной геометро-графической

моделью одной точки эвклидова про-странства.

Изобразительные свойства ортогональных проекций различных точек эвклидова пространства (рис.8.7)

В изобразительных свойствах про-екций точек будем различать их позици-онное и метрическое содержание.

Позиционное содержание описы-вает особенности расположения проек-ций точек относительно оси х₁₂, кодиру-ющие информацию о положении самих точек в пространстве, отнесенном к си-стеме двух плоскостей ортогональных проекций.

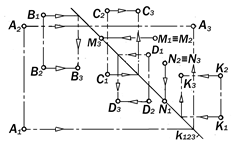
1. Если А₂ выше (­) х₁₂ , А₁ ниже (¯) х_{12 ,} то точка А - в 1-й четверти.

или

1. А₂­ х₁₂ , А₁¯ х₁₂ Þ А Î 1 четв. ;

2. В₂ , В₁­ х₁₂ Þ В Î 2 четв. ;

3. С₂¯ х₁₂ , С₁ ­ х₁₂ Þ С Î 3 четв.;

4. D₂ , D₁ ¯ х₁₂ Þ D Î 4 четв.

5. Е₁ º Е₂ º х₁₂ Þ Е Î х₁₂ ;

6. М₂ ­ х₁₂ , М₁ Î х₁₂ Þ М Î П₂ ;

7. N₂ Î х₁₂ , N₁ ¯ x₁₂ Þ N Î П₁ ;

8. (К₂ º К₁)­ х₁₂ , (L₂ º L₁) ¯ x₁₂ Þ K,LÎd

Если в рис.8.7 убрать ось х₁₂, то ис-чезнут двойные точки А₁₂ , В₁₂ и т.д. и полученный чертёж станет безосным.

Метрическое содержание изобрази-тельных свойств ортогональных проек-ций точек описывает метрику положе-ния изображаемых точек относительно плоскостей проекций.

Если отрезки линий связи между проекциями точек и осью х₁₂ изобра-жают соответствующие участки прое-ирующих лучей от самих точек до пер-пендикулярных к ним плоскостей проек-ций, то эти участки проецируются на те плоскости проекций, к которым они параллельны, в натуральную величину. Поэтому:

1. Расстояние от фронтальной проекции точки до оси проекций х₁₂ равно расстоянию от самой точки до горизонтальной плоскости проекций.

2. Расстояние от горизонтальной

проекции точки до х₁₂ равно расстоя-нию от самой точки до П₂ .

3. Если одна из проекций точки при-надлежит оси х₁₂, то сама точка принад-

лежит одной из плоскостей проекций.

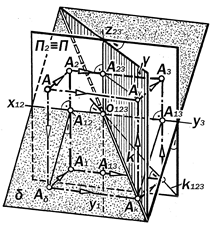
Рис.8.8.Геометрическая модель

точки А в системе трёх плоскостей

проекций

Рис.8.9.Трехкартинные чертежи

различных точек

8.2.2. Трёхкартинный комплексный

чертёж точки

Геометрические модели точек в системе трёх плоскостей проекций

Аппарат получения трёхкартинного комплексного чертежа образуется до-полнением аппарата получения двух-картинного чертежа (см. рис. 8.1) треть-ей, профильной плоскостью проекций (см. рис.8.4). При этом практически тре-тья проекция точки является как бы ис-комой при двух заданных. Отсюда вы-текает постановка важной построите-льной графической задачи: по двум за-данным проекциям объекта постритьего третью проекцию.

Решение этой задачи даёт дополнительную или избыточ-ную информацию о структуре объекта к той необходимой и достаточной, т.е., оптималь-ной информации, которой об-ладают две данные проекции.

Можно также сказать, что

процесс построения третьей

проекции по двум заданным

является процессом п р е о б-

р а з о в а н и я заданных проекций в искомую.

Так как в аппарате полу-чения трёхкартинного компле-ксного чертежа (см. рис.8.4) биссектор-ные плоскости d и g углов совмещения П₁ и П₃ с П₂ º П¢ практически заменяют плоскости проекций П₁ и П₃, то геоме-трическая модель точки А в системе трёх плоскостей проекций приобретает вид, приведенный на рис. 8.8.

Графические модели точек

в системе трёх плоскостей проекций

Определение 8.6.Графическая модель точки в системе трёх плоскостей проекций называется т е р н а р-

н о й.

Определение 8.7.Вся-кая тройка точек как три вершины прямоугольника линий связи, четвёртая вершина которого прина-длежит постоянной пря-мой трехкартинного комплексного

чертежа, называется тернарной мо-

моделью одной точки эвклидова про-странства (рис.8.9).

Изобразительные свойства трёхкартинного комплексного чертежа точки(см. рис.8.9)

Независимо от того, где расположе-на точка А:

1.её горизонтальная проекция А₁ и фронтальная проекция А₂ всегда рас-

полагаются на одной вертикальной линии связи;

2. её фронтальная проекция А₂ и профильная проекция А₃ всегда рас-полагаются на одной горизонтальной линии связи;

3. её горизонтальная А₁ и про- фильная А₃ проекции всегда взаимо-связаны двухзвенной ломаной линией связи с точкой излома на постоянной прямой k₁₂₃ трёхкартинного комплекс-ного чертежа.

Утверждение 8.1.

Независимость

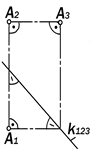
описанной гра-фической конс-трукции прямоу-гольника линий связи между тре-мя проекциями одной точки с по-стоянной прямой k₁₂₃ ,от геометр-рической струк-

Рис. 8.10. Тернарная туры изобража-

модельточки А емого объекта

придаёт ей свойства г р а ф и ч е с-

к о г о а л г о р и т м а п р е о бр а-

з о в а н и я любых двух его проекций в искомую третью.

Приведенная на рис.8.10 графичес-кая конструкция обладает минимально возможным количеством простых гра-фических элементов, т.е., рациональна и поэтому служит основой г р а ф и ч е- с к и х т е х н о л о г и й преоб-разования исходных ортогональных проекций объекта в его третью, иско-мую.

Так как ортогональные проекции являются частным случаем параллель-ных проекций, то следует ожидать, что приведенный графический алгоритм бу-дет справедлив для их общего случая.

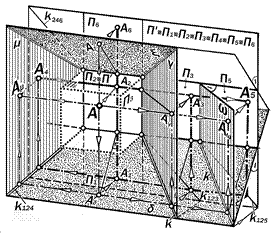
Рис. 8.11.Геометрическая модельаппарата получения многокартинных комплексных чертежей

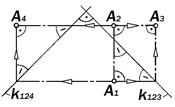
Рис.8.12. Четырёхкартинный

комплексный чертёж точки А

8.2.3. Многокартинные комплексные четрежи точек

В архитектурном и дизайнерском про-ектировании фронтальная проекция объ-екта называется видом спереди или глав-ным фасадом, горизонтальная проекция – видом сверху или планом, профильная – видом слеваили левым боковым фасадом ( располагается правее главного фасада).

Кроме этих видов у объекта есть вид справа или правый боковой фасад (распо-лагается левее главного фасада) и вид сзади или дворовой фа-сад, который располага-ется на чертеже правее левого бокового фасада. Если предположить, что объект находится под го-ризонтальной плоскостью проекций, то возможен вид снизу или плафон, который на чертеже рас-полагается выше главно-го фасада.

Таким образом у пространственного объек-та шесть основных видов как его соответствующих проекций на шесть попар-но параллельных и по тройке перпенди-кулярных плоскостей проекций, образую-щих собой боковую поверхность проекци-онного параллелепипеда или куба (рис.8.11).

В связи с этим можно говорить о четы-рёх, пяти и шестикартинных комплексных чертежах объекта, получаемых последова-тельным совмещением граней куба как плоскостей проекций с плоскостью картины.

Четырёхкартинный комплексный

чертёж точки (рис. 8.12)

Четвертая проекция А₄ - вид справа, располагается левее А ₂, на одной горизон-тальной линии связи с ней и с А₃ , а с А₁ связана двухзвенной линией связи с точкой излома на второй постоянной прямой k₁₂₄ , идущей влево под 45° к вертикальной ли-нии связи.

Определитель четырехкартинного ком-плексного чертежа содержит две взаимно-перпендикулярные его постоянные прямые.

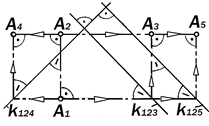
Пятикартинный комплексный

чертёж точки (рис. 8.13)

 

Пятая проекция А₅ - вид сзади, строит-ся по двум, трём или четырем заданным проекциям при помощи третьей постоянной

 

прямой k_{125 ,} параллельной k₁₂₃ .

Определитель пятикартинного компле-ксного чертежа содержит три постоянные прямые, две из которых перпендикулярны к третьей, а поэтому параллельны друг дру-гу.

 

Рис.8.13.Пятикартинный комплексный

чертёж точки А

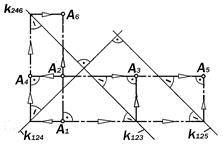
Шестикартинный комплексный чертёж точки А

Шестая проекция А ₆ - вид снизу, строится по двум, трём или четырём заданным про-екциям при помощи четвертой постоянной прямой k_246, либо параллельной, либо сов-падающей с k_123.

Шестикартинный комплексный чертёж является полной системой основных видов изображаемого объекта.

Рис.8.14.Шестикартинный комплексный чертёж точки А

Кроме этих основных видов возможны различные дополнительные виды по задан-ным направлениям проецирования, не сов-падающим с основными направлениями. В этих случаях дополнительные плоскости проекций не будут перпендикулярны в осям основных проекций.

Многокартинные комплексные чертежи информационно являются максимально полными, а двух и трёхкартинные – оптима-льно полными. Поэтому в дальнейшем рас-смотрении содержания системной начерта-тельной геометрии будем преимуществен-но использовать двух и реже трёхкартин-ные комплексные чертежи.

 

 

В о п р о с ы д л я п о в т о р е н и я: