Проверка прочности балки из хрупкого материала
Пример 12.1
a = 3.9м, b = 0.9м, c = 1.2м, 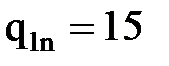 кН/м ,
кН/м , 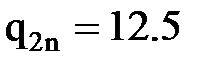 кН/м ,
кН/м ,
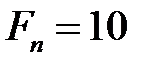 кН,
кН, 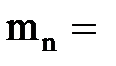 5кН×м,
5кН×м, 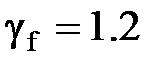 ;
;
сталь: 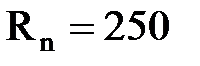 МПа,
МПа, 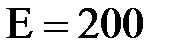 ГПа,
ГПа, 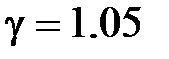 ;
;
древесина: 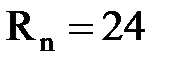 МПа,
МПа, 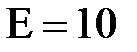 ГПа,
ГПа, 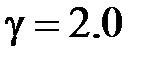 .
.
Расчетные нагрузки:
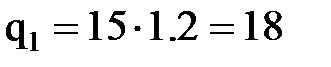 кН/м,
кН/м, 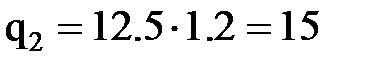 кН/м,
кН/м, 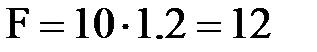 кН ,
кН ,
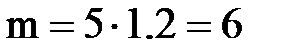 кН×м.
кН×м.
Расчетная схема балки приведена на рис. 12.1
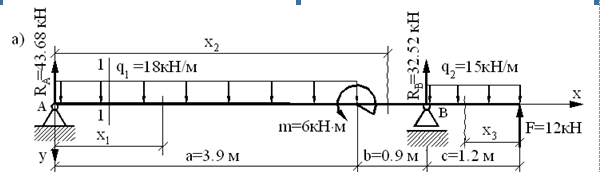
Рис.12.1 Расчетная схема балки
Вычисляем опорные реакции. Из уравнений равновесия получим
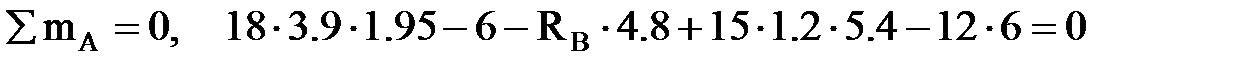 ,
, 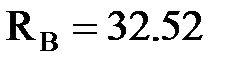 кН;
кН;
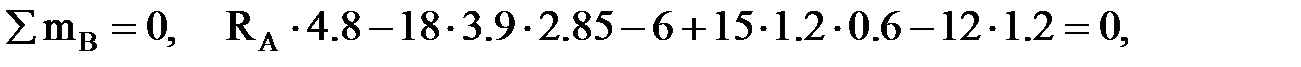
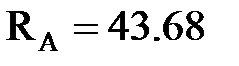 кН.
кН.
Проверка:
 На рис.12.2 показана расчетная схема балки, в которой опорные устройства удалены, а их действие заменено опорными реакциями.
На рис.12.2 показана расчетная схема балки, в которой опорные устройства удалены, а их действие заменено опорными реакциями.
Начало координат примем на левом конце балки. Построение эпюр 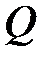 и
и 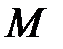 будем выполнять по участкам загружения, которых в рассматриваемом примере три. Граничные точки между участками будем называть узловыми или просто узлы. В качестве узловых принимаются точки приложения сосредоточенных нагрузок (сил и пар), начало или конец распределенной нагрузки, начало или конец балки. Узлы на расчетной схеме занумеруем цифрами 0, 1, 2, 3, а участки между узлами (элементы) цифрами 1,2,3 с прямоугольным окаймлением (рис.12.2).
будем выполнять по участкам загружения, которых в рассматриваемом примере три. Граничные точки между участками будем называть узловыми или просто узлы. В качестве узловых принимаются точки приложения сосредоточенных нагрузок (сил и пар), начало или конец распределенной нагрузки, начало или конец балки. Узлы на расчетной схеме занумеруем цифрами 0, 1, 2, 3, а участки между узлами (элементы) цифрами 1,2,3 с прямоугольным окаймлением (рис.12.2).
Построение эпюр усилий выполним используя уравнения равновесия узлов и элементов балки.
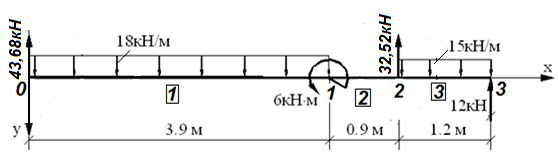
Рис.12.2 Балка с нумерацией узлов и участков (элементов)
Проведем сечение вблизи точки 0 справаивыделимузел 0. Узел должен находится в равновесии под действием внешних (сосредоточенных) и внутренних сил и моментов(рис.12.3). На рис.12.3 через 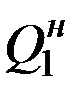 ,
, 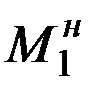 обозначены поперечная сила и изгибающий момент в начале первого элемента (участка) балки.
обозначены поперечная сила и изгибающий момент в начале первого элемента (участка) балки.
Составим уравнения равновесия узла: 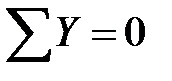 ,
, 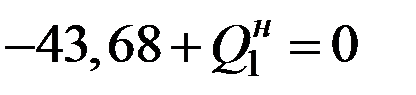 ,
, 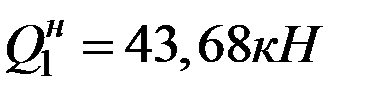 ;
; 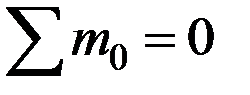 ,
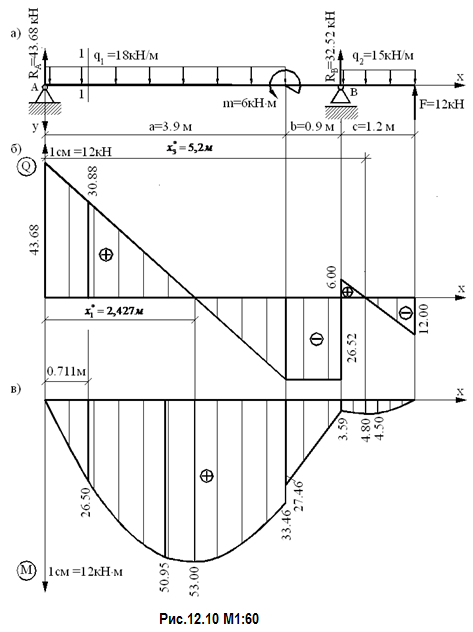
, 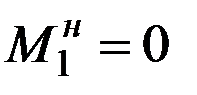 . Таким образом, усилия в начале первого участка известны, их необходимо проставить на эпюрах (рис.12.10) .
. Таким образом, усилия в начале первого участка известны, их необходимо проставить на эпюрах (рис.12.10) .
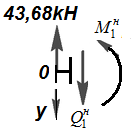 Рис.12.3 Узел 0
Рис.12.3 Узел 0
| 1-й участок 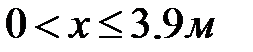
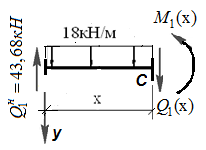 Рис.12.4 Элемент 1-го участка
Рис.12.4 Элемент 1-го участка
|
Выделим элемент балки в пределах первого участка двумя сечениями: первое правее точки 0, а второе в произвольном месте первого участка(рис.12.4). Второе сечение отмечено координатой 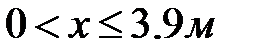 . В начале элемента балки поперечная сила и изгибающий момент известны:
. В начале элемента балки поперечная сила и изгибающий момент известны: 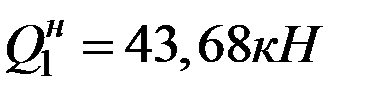 ;
; 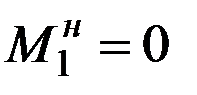 . Вдоль элемента на длине
. Вдоль элемента на длине 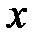 приложена распределенная нагрузка интенсивностью 18кН/м. На правом конце неизвестные внутренние усилия поперечная сила
приложена распределенная нагрузка интенсивностью 18кН/м. На правом конце неизвестные внутренние усилия поперечная сила 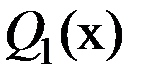 и изгибающий момент
и изгибающий момент 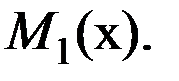 Составим уравнение равновесия элемента:
Составим уравнение равновесия элемента: 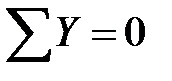 ,
, 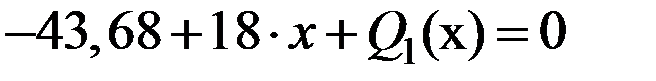 ,
, 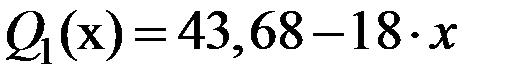 . На концах участка функция
. На концах участка функция 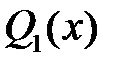 меняет знак, т.е.
меняет знак, т.е. 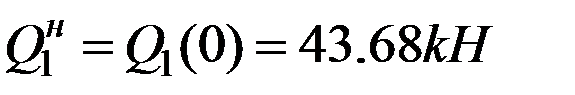 ,
, 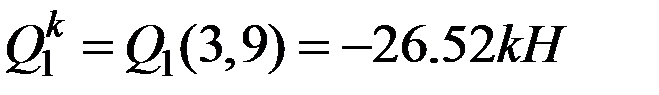 . Найдем положение сечения, в котором
. Найдем положение сечения, в котором 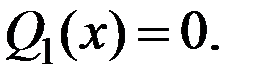 Имеем:
Имеем: 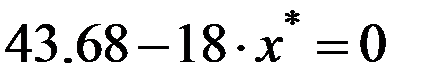 и
и 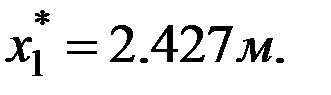 Ординаты проставляем на эпюре. Второе уравнение равновесия:
Ординаты проставляем на эпюре. Второе уравнение равновесия: 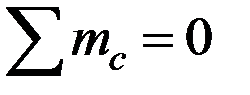 ,
, 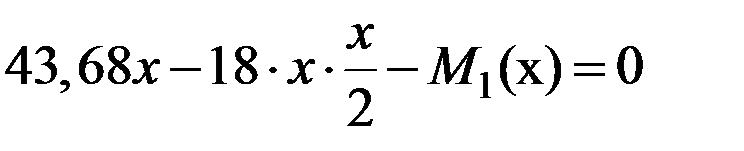 ,
, 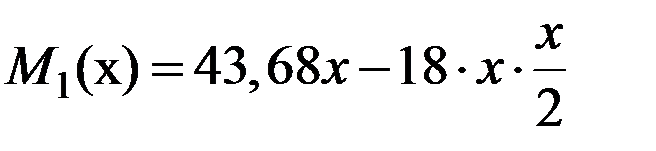 . Проверяем дифференциальную зависимость между изгибающим моментом и поперечной силой
. Проверяем дифференциальную зависимость между изгибающим моментом и поперечной силой 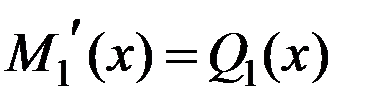 , выполняется. Значения изгибающего момента в характерных точках:
, выполняется. Значения изгибающего момента в характерных точках: 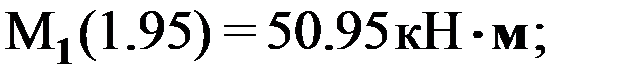
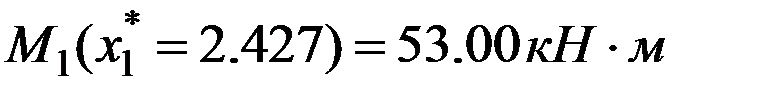 ;
; 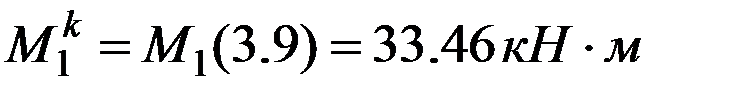 . Строим эпюру изгибающих моментов на первом участке (рис. 12.10)
. Строим эпюру изгибающих моментов на первом участке (рис. 12.10)
Вырезаем узел 1 (рис.12.5). Показываем внутренние усилия в элементах, прилегающих к узлу и приложенную в узле пару сил 6 кНм.Слева от узла 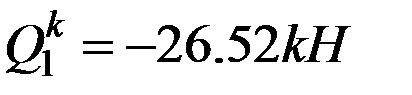 и
и 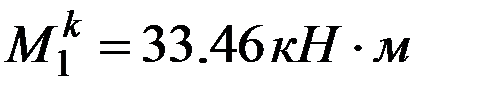 . Справа от узла в сечении действуют: поперечная сила
. Справа от узла в сечении действуют: поперечная сила 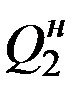 и изгибающий момент
и изгибающий момент 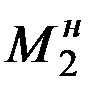 в начале 2-го участка.
в начале 2-го участка.
Составим равнения равновесия узла: 1: 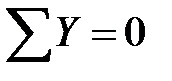 ,
, 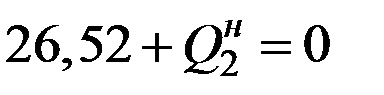 ,
, 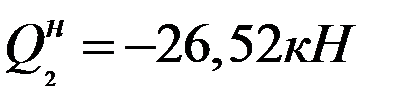 ;
; 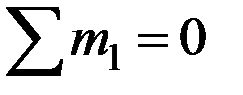 ,
, 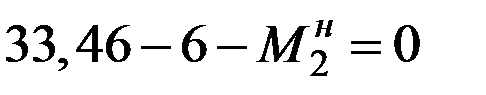 ,
, 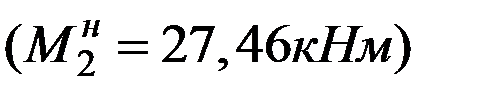 . Таким образом, усилия в начале 2-го участка известны, проставляем их значения на эпюрах.
. Таким образом, усилия в начале 2-го участка известны, проставляем их значения на эпюрах.

Рис. 12.2 Балка с нумерацией узлов и участков (повторение рисунка)
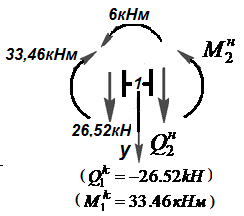 Рис.12.5 Узел 1
Рис.12.5 Узел 1
| 2-ой участок 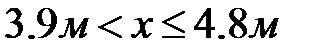 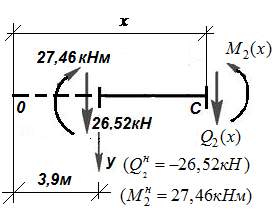 Рис.12. 6 Элемент 2-го участка
Рис.12. 6 Элемент 2-го участка
|
Выделим элемент балки в пределах 2-го участка двумя сечениями: первое правее точки 1, а второе в произвольном месте 2-го участка 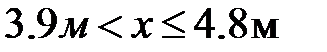 (рис.12.6). Составим уравнение равновесия элемента:
(рис.12.6). Составим уравнение равновесия элемента: 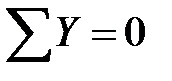 ,
, 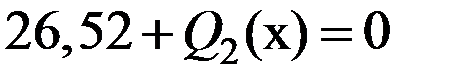 ,
, 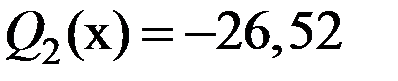 кН,
кН, 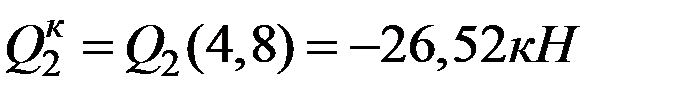 ,
,
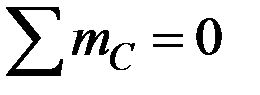 ,
, 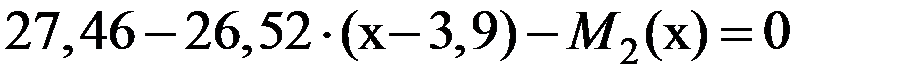 ,
, 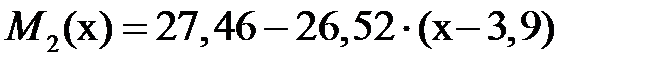 . Проверяем дифференциальную зависимость
. Проверяем дифференциальную зависимость 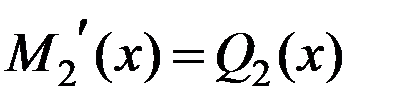 , выполняется. Значение на конце участка
, выполняется. Значение на конце участка 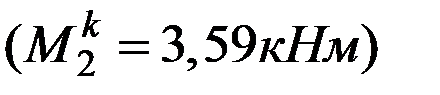 .
.
Вырезаем узел 2 (рис.12.7). Показываем внутренние усилия в элементах прилегающих к узлу и приложенную в узле внешнюю силу 32,52 кН.
Составим равнения равновесия узла 2: 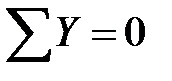 ,
, 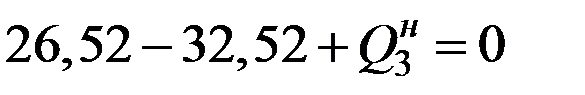 ,
, 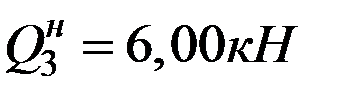 ,
, 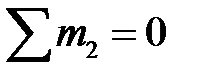 ,
, 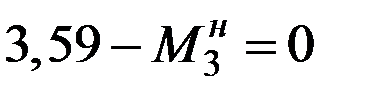 ,
, 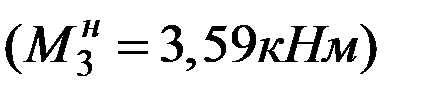 . Таким образом, усилия в начале 3-го участка известны.
. Таким образом, усилия в начале 3-го участка известны.
Выделим элемент балки в пределах 3-го участка двумя сечениями: первое правее точки 2, а второе в произвольном месте 3-го участка 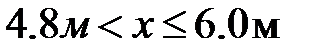 (рис.12.8).
(рис.12.8).
Составим уравнение равновесия элемента: 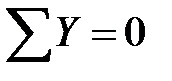 ,
, 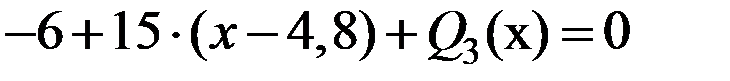 ,
,
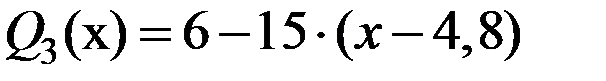 ,
, 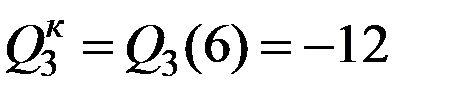 кН. По концам участка функция
кН. По концам участка функция 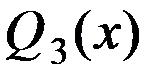 меняет знак
меняет знак 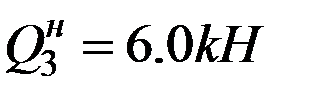 ,
, 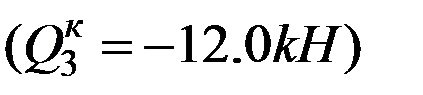 . Найдем положение сечения, в котором
. Найдем положение сечения, в котором 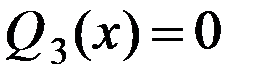 Имеем:
Имеем: 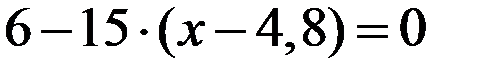 и
и 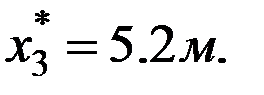 Сумма моментов всех сил относительно точки
Сумма моментов всех сил относительно точки 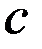 :
: 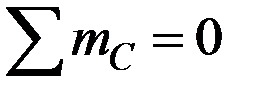 ,
, 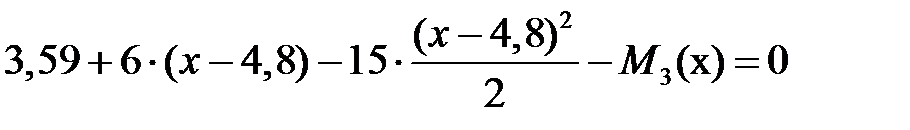 ,
,

Рис. 12.2 Балка с нумерацией узлов и участков (повторение рисунка)
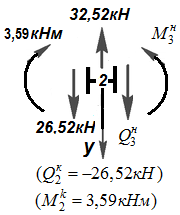 Рис.12.7 Узел 2
Рис.12.7 Узел 2
| 3-й участок 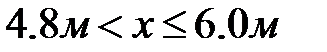 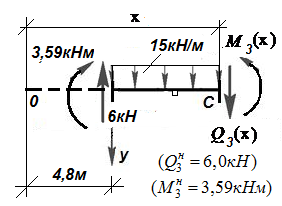 Рис. 12.8 Элемент 3-го участка
Рис. 12.8 Элемент 3-го участка
|
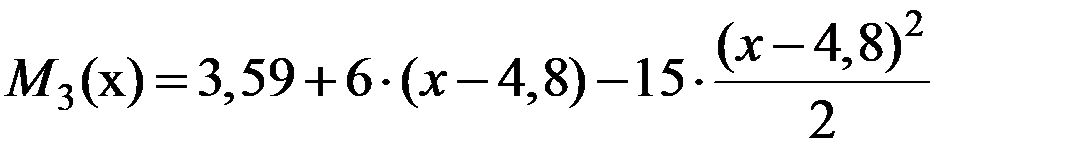 . Проверяем, дифференциальную зависимость
. Проверяем, дифференциальную зависимость 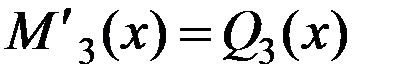 , выполняется. Значения изгибающего момента в характерных точках 3-го участка:
, выполняется. Значения изгибающего момента в характерных точках 3-го участка: 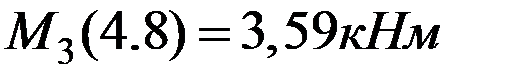 ;
; 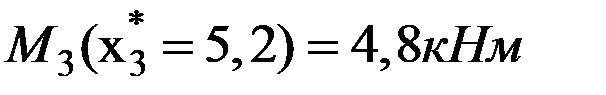 ;
; 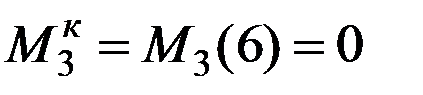 . Строим эпюры (рис.12.10).
. Строим эпюры (рис.12.10).
Заметим, что при построении эпюр для узла 3 уравнения равновесия не составлялись. Эти уравнения служат для проверки. Узел должен находиться в равновесии под действием внешних (сосредоточенных) и внутренних искомых сил и моментов(рис.12.9).
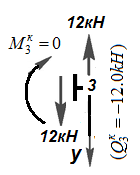 Рис12..9 Узел 3
Рис12..9 Узел 3
| 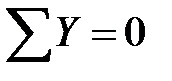 , , 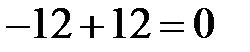 . .
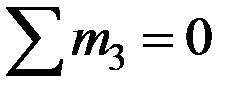 , 0=0. , 0=0.
|
Проверка прочности балки из хрупкого материала
Пример 12. 2. [1].Проверить прочность балки таврового сечения (рис.12.11), изготовленной из чугуна. Расчетное сопротивление на растяжение 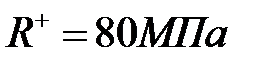 , расчетное сопротивление на сжатие
, расчетное сопротивление на сжатие 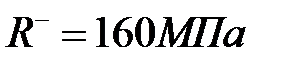 .
.
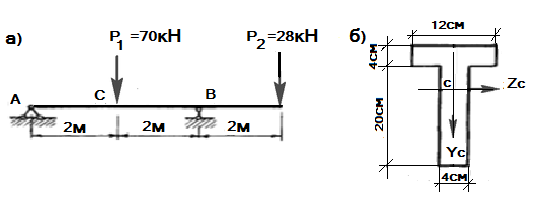
Рис.12.11 Балка таврового сечения
Решение. Определяем опорные реакции:
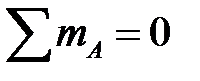 ,
, 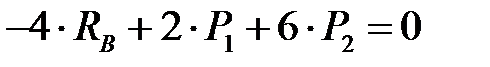 ,
, 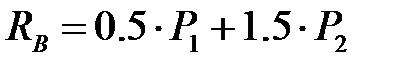 ,
, 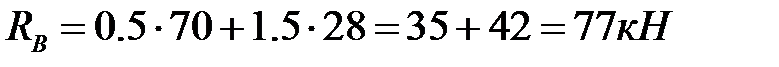 ;
;
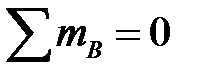 ,
, 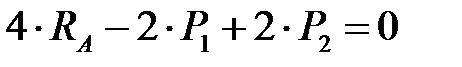 ,
, 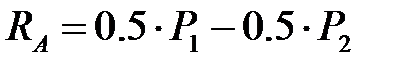 ,
, 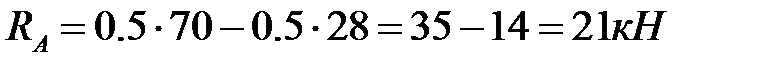 .
.
Строим эпюры поперечных сил 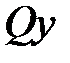 и изгибающих моментов
и изгибающих моментов 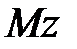 (рис.12.12).
(рис.12.12).
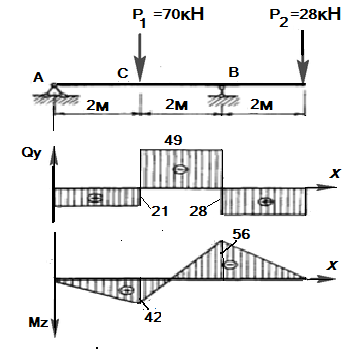
Рис.12.12 Эпюры поперечных сил и изгибающих моментов
Вычисляем статический момент тавра относительно вспомогательной оси 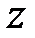 (рис.5а)
(рис.5а) 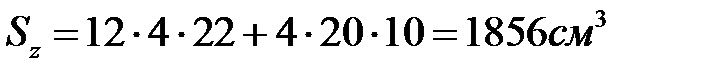 . Площадь сечения
. Площадь сечения 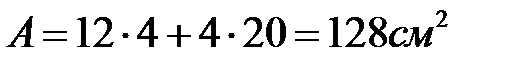 . Координата центра тяжести
. Координата центра тяжести 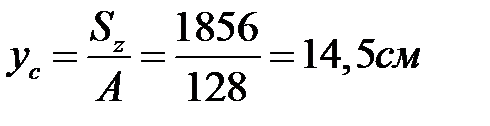 . Главный центральный момент инерции
. Главный центральный момент инерции
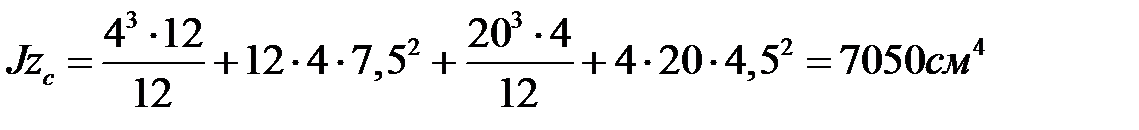 .
.
Координаты точек сечения наиболее удаленных от нейтральной оси 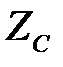 :
: 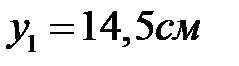 ,
, 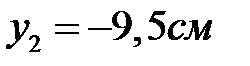 .
.
Моменты сопротивления сечения относительно нейтральной оси 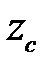 для нижних и верхних волокон
для нижних и верхних волокон 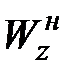 ,
, 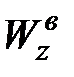 :
:
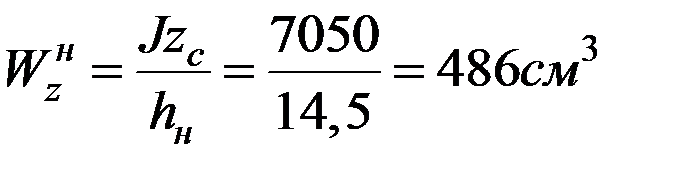 ,
, 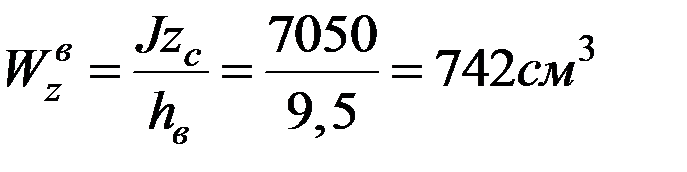
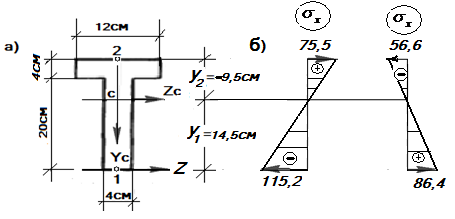
Рис. 12.13 Эпюры нормальных напряжений в опасных сечениях
При проверке прочности балки из хрупкого материала опасными являются сечения с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине отрицательным изгибающим моментом. В данной задаче таковыми являются сечение 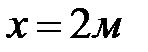 ,
, 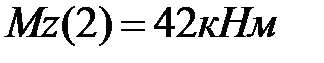 и сечение
и сечение 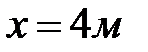 ,
, 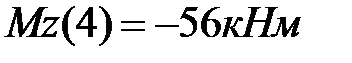 .
.
Строим эпюры нормальных напряжений в опасных сечениях (рис.12.13,б).
1) Сечение 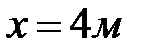 с наибольшим по абсолютной величине изгибающим моментом. Нормальные напряжения в точках 1 и 2:
с наибольшим по абсолютной величине изгибающим моментом. Нормальные напряжения в точках 1 и 2:
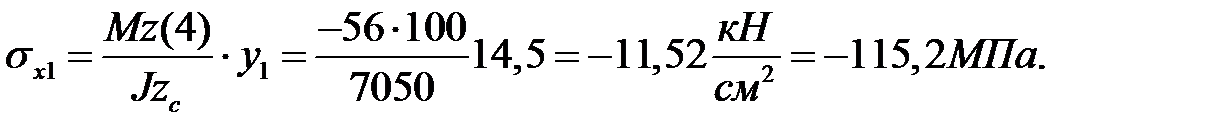 ,
, 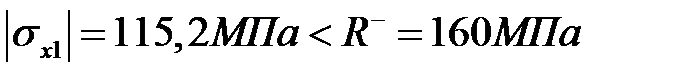 , прочность обеспечена.
, прочность обеспечена.
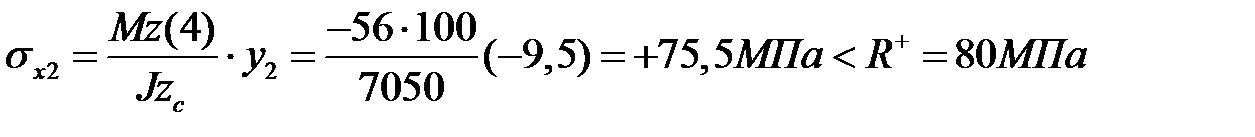 , прочность обеспечена.
, прочность обеспечена.
2) Сечение 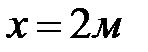 с наибольшим положительным изгибающим моментом. Нормальные напряжения в точках 1 и 2:
с наибольшим положительным изгибающим моментом. Нормальные напряжения в точках 1 и 2:
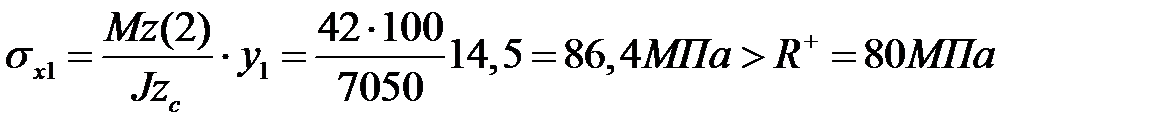 , прочность не обеспечена.
, прочность не обеспечена.
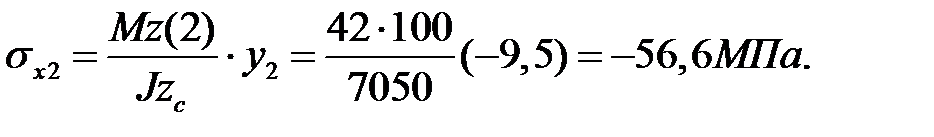
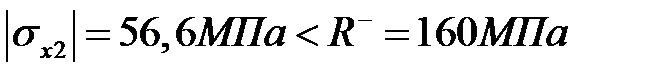 , прочность обеспечена.
, прочность обеспечена.

Дата добавления: 2017-09-01; просмотров: 1106;











