Вывод формул для нормальных напряжений в поперечных сечениях
Пусть в рассматриваемом сечении известны усилия: 
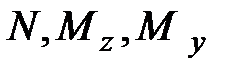 . Выразим через них напряжения
. Выразим через них напряжения 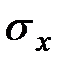 . С учетом формул (9.1), (9.2), (3.6) получим:
. С учетом формул (9.1), (9.2), (3.6) получим:
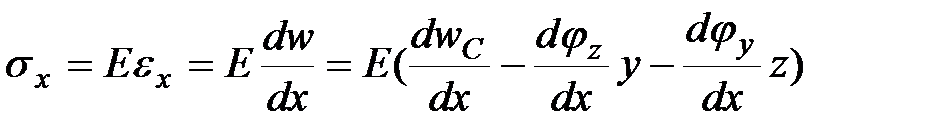
| (9.3) |
Обозначим для данного сечения постоянные:
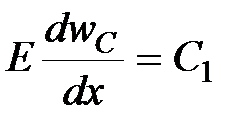 ; ;
|  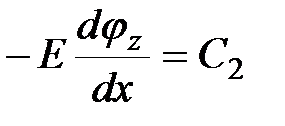 ; ;
| 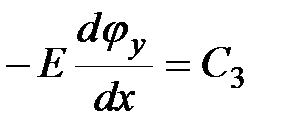 . .
| (9.4) |
Перепишем (9.3) с учетом обозначений (9.4)
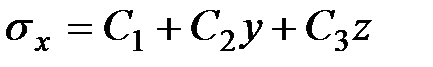
| (9.5) |
Формула (9.5) показывает, что 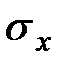 изменяется по закону плоскости, определяемой тремя константами:
изменяется по закону плоскости, определяемой тремя константами: 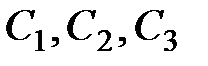 . Для определения констант необходимо потребовать, чтобы
. Для определения констант необходимо потребовать, чтобы 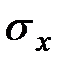 приводились к трем силовым факторам (см. формулы 1.2)
приводились к трем силовым факторам (см. формулы 1.2)
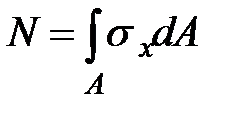 
| 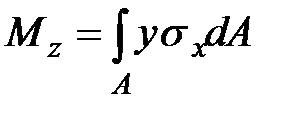
| 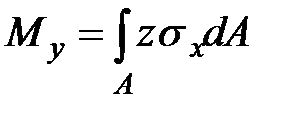
| (9.6) |
Формулы (9.6) следуют из рис. 9.4
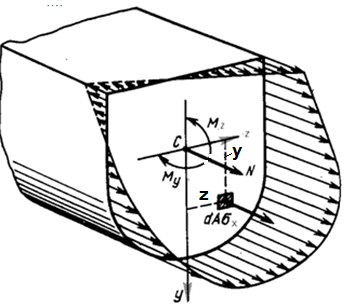
Рис. 9.4 Напряжения 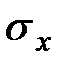 в поперечном сечении распределены по линейному закону
в поперечном сечении распределены по линейному закону
Подставляем последовательно выражение для напряжений(9.5) в формулы (9.6) . В результате получим:
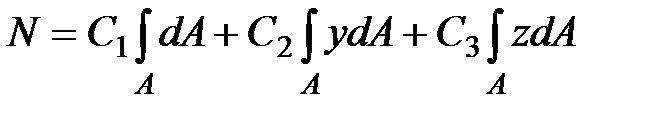
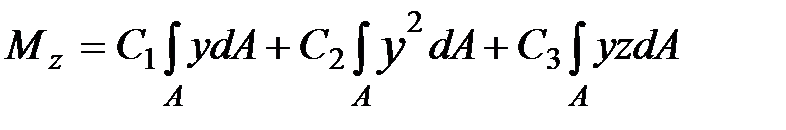
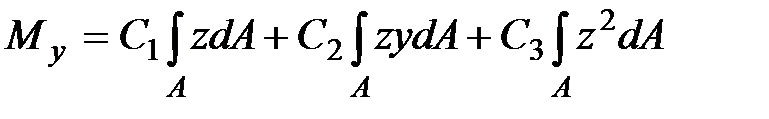
| (9.7) |
С учетом выражений для геометрических характеристик поперечных сечений будем иметь:
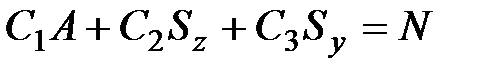 ; ;
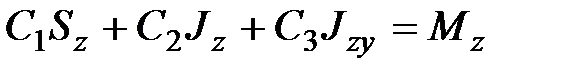 ; ;
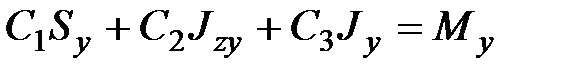 . .
| (9.8) |
В уравнениях (9.8) введены следующие обозначения: площадь и статические моменты площади относительно осей z и y
A= 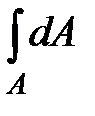 ; ;
| 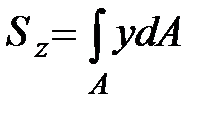 ; ;
| 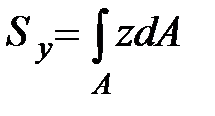 ; ;
| (9.9) |
осевые и центробежный моменты инерции
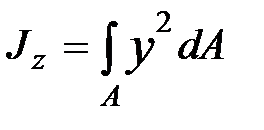 ; ;
| 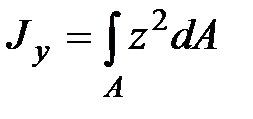 ; ;
| 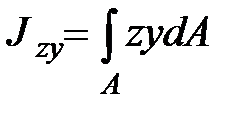 . .
| (9.10) |
Будем считать, что оси z,y главные центральные оси, тогда
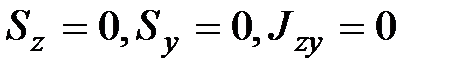 . .
| (9.11) |
В результате система (9.8) распадается на три независимых уравнения, из которых находим:
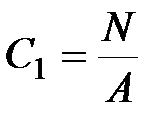
| 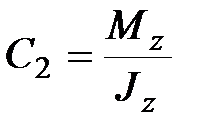
| 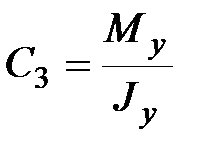
| (9.12) |
Подстановка выражений (9.12) в формулу (9.5) дает общую формулу для нормальных напряжений
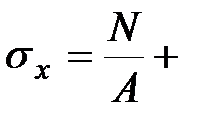 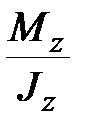 y+ y+ 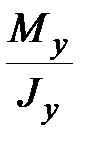 z z
| (9.13) |
Плоскости z-x, y-x, содержащие ось стержня и одну из главных осей сечения, называются главными плоскостями изгиба стержня.
В формуле (9.13) растягивающая продольная сила N положительна, изгибающие моменты 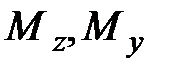 также положительны, если они в точке, принадлежащей первой четверти осей координат (гдеz>0,y>0), вызывают растягивающие напряжения (см.рис.9.4).
также положительны, если они в точке, принадлежащей первой четверти осей координат (гдеz>0,y>0), вызывают растягивающие напряжения (см.рис.9.4).
Дата добавления: 2017-09-01; просмотров: 1251;











