Процедуры оценки векторов
В основе этих процедур лежит предположение, что ЛПР может непосредственно сравнивать решения, предъявляемые ему в виде векторов в пространстве критериев, и последовательно искать в этом пространстве наилучший вектор.
Процедура Дайера-Джиофриона (Д - Д) ЧМП оценки векторов начинается с выбора начальной точки 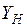 в пространстве критериев (рис. 13).
в пространстве критериев (рис. 13).
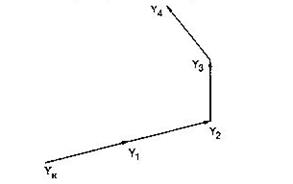
Рисунок 13. Поиск решения в пространстве критериев.
В этой точке ЛПР определяет градиент глобальной целевой функции. Один из критериев считается опорным. Берется небольшое изменение для значения этого критерия (в сторону улучшения) от начального. Перед ЛПР ставятся вопросы типа: какое изменение по иному критерию эквивалентно заданному изменению опорного критерия? Ответы ЛПР определяют вектор (направление), вдоль которого изменение глобального критерия будет наиболее эффективным. Вдоль этого направления реализуют шаг определенной величины, и получают новые значения по всем частным критериям. ЛПР сравнивает полученный вектор (совокупность новых решений) с первоначальным решением (соответствующим начальной точке). Далее перед ЛПР ставится вопрос: какое из решений лучше? Если новое решение 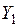 лучше, то делается еще шаг вдоль этого же направления и вычисляется решение
лучше, то делается еще шаг вдоль этого же направления и вычисляется решение 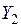 . Далее
. Далее 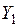 и
и 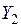 предъявляют ЛПР. Если
предъявляют ЛПР. Если 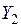 лучше, то делается еще шаг в прежнем направлении и т.д. Если
лучше, то делается еще шаг в прежнем направлении и т.д. Если 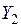 хуже, чем
хуже, чем 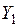 , то в точке
, то в точке 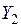 определяют новый градиент (направление) изменения глобальной целевой функции (см. рисунок 13) и т.д. Процедура заканчивается, если ЛПР признает очередное решение вполне для него удовлетворительным.
определяют новый градиент (направление) изменения глобальной целевой функции (см. рисунок 13) и т.д. Процедура заканчивается, если ЛПР признает очередное решение вполне для него удовлетворительным.
В отличие от прямых методов в ЧМП Д - Д реализован систематический поиск, помогающий ЛПР выбрать наилучшее решение. Недостатком ЧМП оценки векторов является предположение, что ЛПР может безошибочно определять градиент целевой функции. Отмечалось, что, работая с малыми приращениями критериев, ЛПР будет накапливать ошибки.
Дата добавления: 2017-09-01; просмотров: 1598;











