Предельная нагрузка при изгибе балки из упругопластического материала. Подбор сечения.

Практический интерес представляет задача об определении несущей способности балки, т.е. вычисление предельной нагрузки, которую она может выдержать. Рассмотрим ее определение в случае плоского изгиба.

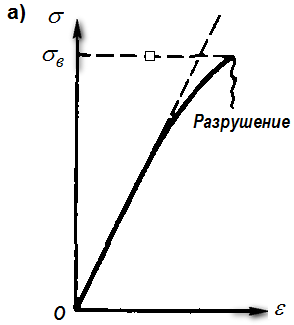
Для хрупкого материала, работающего вплоть до самого момента разрушения почти линейно упруго (рис. 10.4,а) предельная нагрузка определяется из формулы

,

,

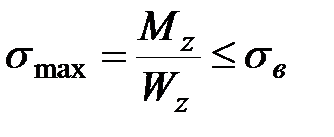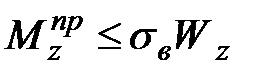(10.7)

где 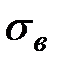- временное сопротивление (предел прочности) материала.

Сложнее обстоит дело с упругопластическим материалом. В целях упрощения задачи для материала балки примем в качестве расчетной диаграмму Прандтля (рис 10.4,б).

Пока напряжения 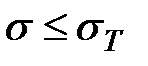материал работает линейно-упруго и применима формула (10.1). При достижении в крайних точках опасного сечения напряжений 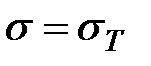возникает текучесть и продольное волокно в этих точках деформируется при постоянных напряжениях .

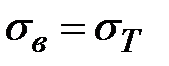Рис. 10.4 Диаграмма напряжений, материал хрупкий. Упругопластическая работа материала, диаграмма Прандтля

Рассмотрим стадии развития деформаций, возникающие в балке, с ростом нагрузки вплоть до исчерпания несущей способности (рис.10.5) .

При постепенном возрастании внешней силы 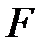упругая стадия работы заканчивается, когда в крайних точках опасного сечения возникают напряжения равные пределу текучести.

,

,

,

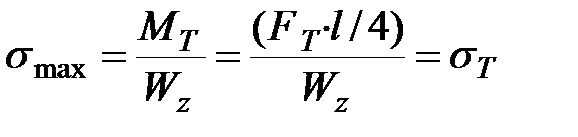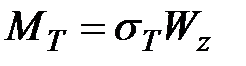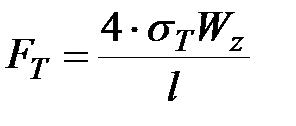(10.8)

где 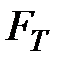- нагрузка начала текучести.

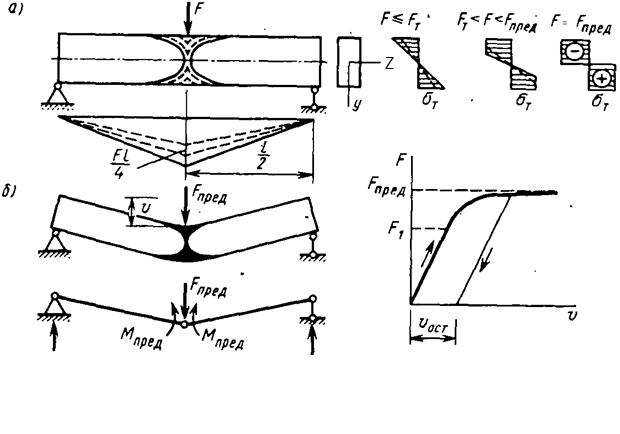Рис.10.5

При дальнейшем росте силы наступает упругопластическая стадия работы балки. Зона текучести будет расширяться от указанных крайних точек, а эпюра напряжений 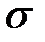будет трансформироваться ( ).

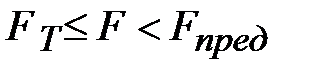Когда внешняя сила станет равной предельной 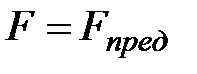, эпюра напряжений 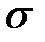переходит в ступенчатую эпюру с ординатами 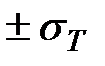. В балке образуется пластический шарнир .

Состояние сечения, когда во всех его точках развиваются пластические деформации, называют пластическим шарниром.

При этом балка превращается в механизм, продолжающий увеличивать прогибы 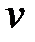при постоянной внешней нагрузке 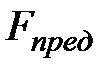. Такое состояние называется пластическим механизмом. 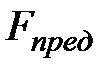- нагрузка образования пластического механизма. При разгрузке балки образуется остаточный прогиб .

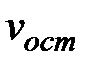В поперечном сечении, где образовался пластический шарнир, внутренний момент обозначим 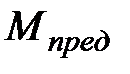и назовем его пластическим предельным моментом.

Выразим через 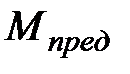предельную нагрузку

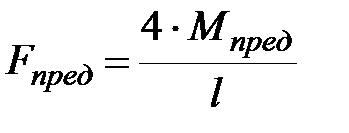
(10.9)

Таким образом, в опасном сечении балки напряженное состояние проходит три стадии: линейно-упругая ( 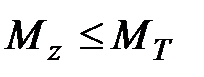); упругопластическая ( 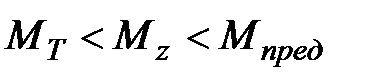); чисто пластическая ( ).

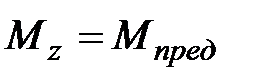Определим величину пластического предельного момента. Пусть поперечное сечение балки имеет одну ось симметрии (рис. 10.6).

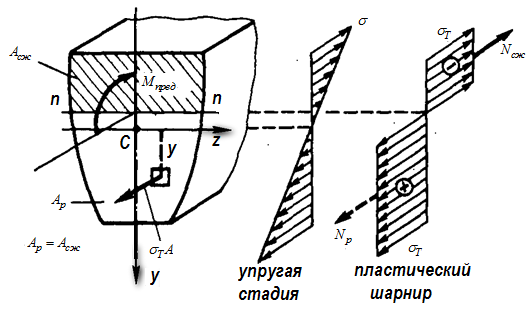
Рис. 10.6 Пластический шарнир в несимметричном сечении

При работе балки в линейно-упругой стадии нейтральная линия 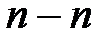совпадает с осью z. В общем случае при образовании пластического шарнира нейтральная линия 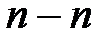смещается от центра тяжести сечения С.

Всё сечение делиться на две части:

1) площадью 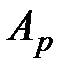, где действуют растягивающие напряжения 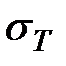и соответствующая продольная сила ;

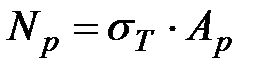2) площадью 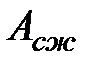, где действуют напряжения сжатия 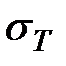и соответствующая продольная сила ;

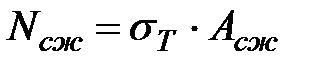Так как суммарная продольная сила в сечении при поперечном изгибе равна нулю, то из этого условия следует:

,

.

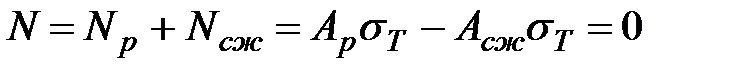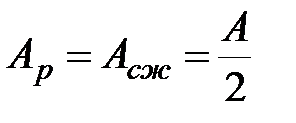(10.10)

При образовании пластического шарнира нейтральная линия делит площадь поперечного сечения на две равновеликие части.

И сходя из вида эпюры нормальных напряжений (рис 10.6,б), внутренний момент 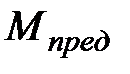найдем по формулам:

,

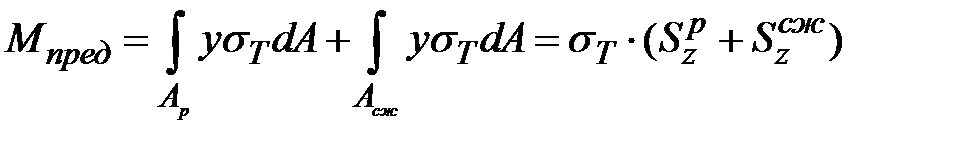(10.11)

где 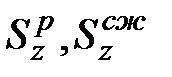- статические моменты растянутой и сжатой частей сечения (взятые по абсолютной величине):

,

.

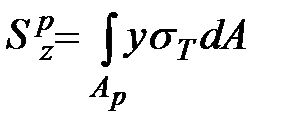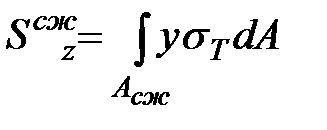(10.12)

Геометрическая характеристика

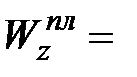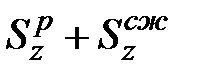
(10.13)

называется пластическим моментом сопротивления ( 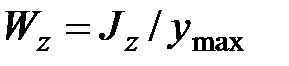-момент сопротивления при работе материала балки в упругой стадии).

Таким образом, выражение для предельного момента имеет вид

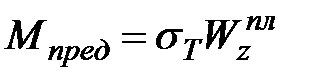
(10.14)

Обозначим через 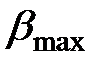коэффициент, показывающий во сколько раз должна возрасти нагрузка от момента появления текучести в балке до полного исчерпания ею несущей способности 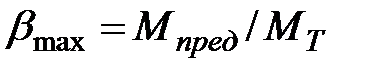. С учетом формул (10.8), (10.14) получим

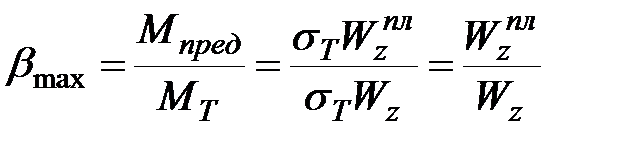
(10.15)

Если сечение имеет две оси симметрии, то

,

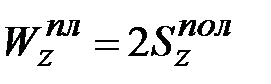(10.16)

где 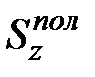- статистический момент половины поперечного сечения.

Для прямоугольного сечения

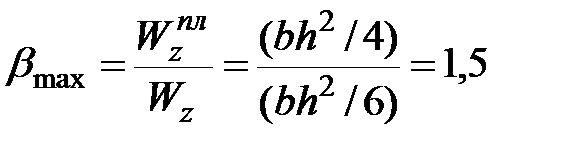
(10.17)

Для круглого сечения 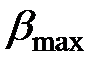=1,7. Для двутавра 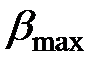=1,17.

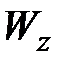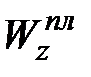В общем, можно заметить, чем рациональнее форма сечения по обычной оценке напряжений, тем ближе значение к и тем меньше различие между расчетами по напряжениям и по предельным нагрузкам.

Формула для подбора поперечного сечения балки из пластичного материала имеет вид

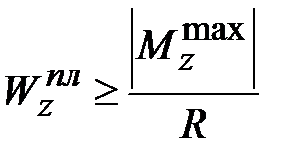
(10.18)

Подберем поперечное сечение двутавра для балки из примера 10.1 (рис.10.2), используя расчеты по предельным нагрузкам:

, , .

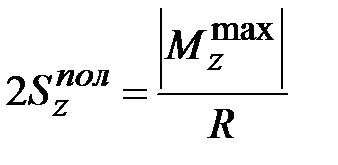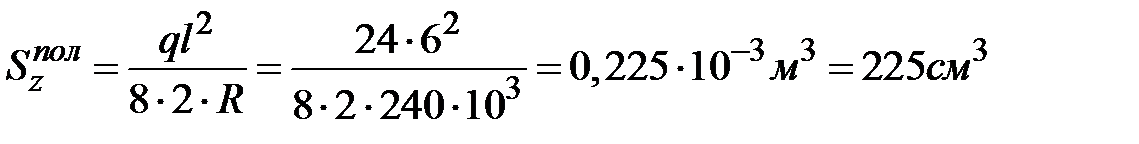Из таблицы сортамента (по ГОСТ 8239-89) находим двутавр №30, для которого статический момент полусечения (половины сечения ) 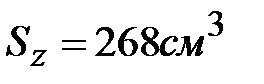. Таким образом, расчеты по методу предельных состояний и методу разрушающих нагрузок дали один и тот же результат.