ОСНОВЫ ТЕОРИИ ФИНАНСОВЫХ РАСЧЕТОВ

Деньги на финансовом рынке выступают в роли товара. Процентами (процентными деньгами) называют сумму доходов от предоставления денег в долг в различных формах (открытие депозитных счетов, выдача кредитов, покупка облигаций и т.д.). Сумма процентов ( 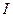) зависит от суммы долга ( 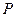), срока на который он выдан ( 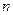- лет или 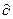- дней), вида и величины процентной ставки ( 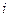– ставка % из расчета годовых, 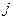– ставка % за период, d – учетная ставка % из расчета годовых, в том числе, формулы простых или сложных процентов), используемой практики начисления процентов (немецкой, французской, английской).

Сумму основного долга вместе с начисленными процентами называют наращенной суммой долга ( 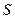). Увеличение суммы долга за счёт присоединения к ней суммы периодически начисляемых процентов называют наращением. Интервал времени, за который начисляют проценты, называют периодом наращения.

Проценты могут выплачиваться по мере начисления или в конце срока. Если проценты периодически начисляются на одну и ту же сумму долга, то в этом случае речь идёт о простых процентах и простых процентных ставках. Если проценты начисляются на сумму основного долга и начисленных за предыдущие периоды процентов, то в этом случае речь идёт о сложных процентах и сложных процентных ставках.

Простые проценты

Сумма процентов за год при начислении простых процентов определяется по формуле:

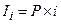(1.1.)

где 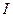- сумма начисленных процентов, руб.;

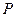- первоначальная сумма долга, руб.;

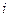- ставка простых процентов из расчёта годовых, в долях единицы.

То же за период меньший чем год (день, месяц, квартал, полугодие):

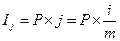(1.2.)

где 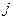- ставка простых процентов за период (день, месяц, квартал, полугодие);

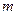- число периодов начисления процентов в году (соответственно 365, 12, 4, 2). Определяется по формуле:

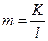(1.3.)

где 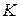- временная база, обычно количество дней в году (или в месяцах);

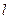- длительность одного периода наращения в днях (месяцах).

Сумма процентов за год в этом случае будет определяться по формуле:

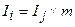(1.4.)

Если период наращения составляет 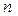лет, то сумма начисленных процентов определяется по формуле:

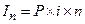(1.5.)

Наращенная сумма долга ( 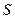), т.е. сумма долга вместе с начисленными процентами определяется по формуле:

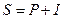(1.6.) или 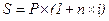(1.7.)

Если период наращения выражается в днях, то в формулы для определения суммы начисленных процентов или наращенной суммы долга вместо n следует подставить отношение:

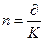(1.8.)

где 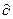– период наращения в днях;

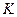- временная база, или количество дней в году (365, 366, 360).

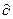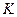В банковской практике различных стран эти два показателя ( и ) определяются по-разному. В германской практике подсчёт числа дней производится приближённо из расчёта продолжительности каждого полного месяца в 30 дней. Временная база (продолжительность года) берётся равной 360 дням. При использовании французской практики количество дней полного месяца считается точно, т. е. берётся равным их фактической календарной длительности (28, 29, 30 или 31 день). Временная база - 360 дней. При английской практике и период наращения в днях, и продолжительность года определяются точно. Исходя из этого, определяются соответственно:

1) Обыкновенные проценты с приближённым числом дней ссуды (германская практика):

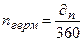(1.9.)

2) Обыкновенные проценты с точным числом дней ссуды (французская практика):

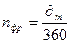(1.10.)

3) Точные проценты с точным числом дней ссуды (английская практика):

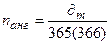(1.11.)

P.S.: Точное число дней периода наращения можно определить по таблице «Порядковые номера дней в году» вычитанием из порядкового номера даты окончания периода наращения порядкового номера даты его начала (см. табл. в приложении)

Если ставки процентов изменяются в течение срока хранения вклада, то сумму начисленных процентов можно определить как сумму процентов, начисленных для каждого периода наращения, на котором действовала определённая ставка процентов.

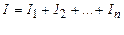(1.12.)

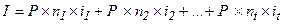(1.13.)

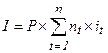(1.14.)

Наращенная сумма в этом случае определяется по формуле:

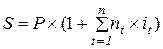(1.15.) или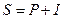

где 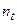- период времени, в течение которого действовала ставка .

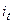При изменении суммы вклада в течение срока хранения (или периода наращения) общая сумма процентов за весь срок может быть определена как сумма процентов, начисленных для каждого периода начисления, на котором сумма на счёте была постоянна:

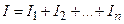
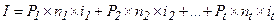(1.16.)

Наращенная сумма определяется по формуле:

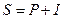
В практике банков для начисления процентов используется также методика с вычислением так называемых процентных чисел.

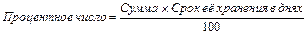(1.17.)

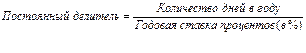(1.18.)

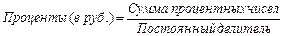(1.19.)

Используя формулу

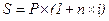
можно решать обратную задачу - по известной наращенной сумме определять сумму первоначального взноса. Данная операция называется дисконтированием по простой процентной ставке.

Известны:

1) математическое дисконтирование:

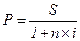(1.20.) или 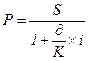(1.21.) или 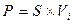(1.22.)

где Vi- коэффициент дисконтирования;

2) банковский учёт:

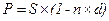(1.23.) или 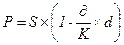(1.24.)

где 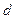-простая учётная ставка.

Как правило, в операции дисконтирования 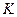= 360 дней.

Из формул:

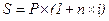или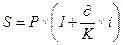

можно при прочих заданных условиях определить, соответственно, период наращения в годах и днях, ставку простых процентов. Формулы предлагается вывести самостоятельно путём математических преобразований формул для определения наращенной суммы.

Сложные проценты

Как было отмечено ранее, база начисления простых процентов не изменяется в течение всего периода наращения и наращенную сумму можно определить по формуле:

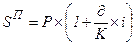
База начисления сложных процентов, в отличие от простых, возрастает после каждого периода наращения на сумму начисленных за предыдущий период процентов (естественно, в том случае, если они не будут выплачены вкладчику). Наращенная сумма определяется по формуле:

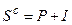(1.25.) или 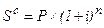(1.26.)

Сумму начисленных процентов можно определить по формуле:

(1.27.)

Если период наращения не является целым числом (например, n=3,5 года), то множитель наращения 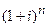можно определить двумя способами:

1) используя нецелый показатель степени. Тогда наращенная сумма определяется по формуле:

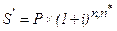(1.28.)

где 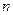- целая часть числа,

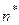- дробная часть числа,

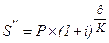(1.29.)

2) смешанный метод (дает большую, по сравнению с предыдущим методом, итоговую сумму):

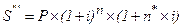(1.30.)

Начисление сложных процентов может осуществляться несколько раз в году (например, ежедневно, ежемесячно, ежеквартально, по полугодиям). В расчётах, в этом случае, используют либо ставку процентов за период, либо годовую ставку процентов, исходя из которой определяется ставка процентов за период (иными словами, номинальная ставка процента). Наращенная сумма в этих случаях может быть определена по формулам:

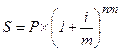(1.31.)

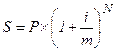(1.32.)

где 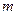- число периодов начисления процентов в году. Определяется независимо от длительности периода наращения по формуле:

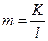(1.33.)

где l – длительность одного периода наращения в днях (месяцах);

K – временная база в днях или месяцах.

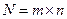(1.34.) -общее число периодов начисления процентов за весь срок хранения.

Сумма начисленных процентов определяется по формулам:

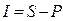(1.35.)

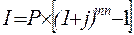(1.36.)

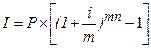(1.37.)

Из формул для определения наращенной суммы при начислении сложных процентов один или несколько раз в году можно, при прочих известных условиях, вывести формулу для определения:

1) срока хранения вклада для накопления заданной суммы:

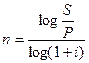(1.38.)

2) ставки сложных процентов:

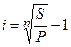(1.39.)

3) значения первоначальной суммы вклада, т.е. выполнить операцию дисконтирования будущей суммы:

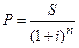(1.40.)

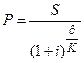(1.41.)

При начислении сложных процентов несколько раз в году дисконтированная сумма будет определяться по формуле:

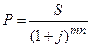(1.42.)

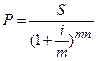(1.43.)

Финансовые ренты

Последовательность денежных поступлений, осуществляемых равными суммами через равные периоды времени, называют постоянной финансовой рентой.

Рента характеризуется следующими параметрами:

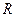- член ренты (размер отдельного платежа);

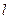- период ренты (временной интервал между двумя последовательными платежами);

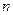- срок ренты (время от начала первого периода ренты до конца последнего периода);

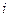- годовая процентная ставка;

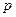-число платежей (взносов) в течение года;

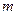- число начислений процентов в течение года.

По количеству выплат членов ренты на протяжении года ренты делятся на:

· годовые (выплата один раз в году);

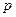· - срочные ( выплаты несколько раз в году, 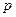- раз);

· ренты с периодом более года;

Эти виды рент называются дискретными. Если же платежи производятся очень часто, то такие ренты рассматриваются как непрерывные.

По количеству начислений процентов на протяжении года различают:

· ренты с ежегодным начислением;

· ренты с начислением процентов несколько раз в году ( 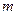- раз);

· ренты с непрерывным начислением процентов.

Частота начисления процентов может не совпадать с частотой уплат (взносов).

По величине своих членов ренты делятся на постоянные (с одинаковыми по величине платежами) и переменные.

По вероятности выплат ренты делятся на верные и условные. Верные ренты подлежат безусловной уплате. Число членов такой ренты заранее известно. Выплата условной ренты ставится в зависимость от наступления некоторого случайного события. Число членов такой ренты заранее неизвестно.

По количеству членов различают ренты с конечным числом членов, т.е. ограниченные по срокам ренты и бесконечные (вечные) ренты.

По моменту выплат платежей в пределах периода различают:

· ренту постнумерандо (обыкновенная), когда платежи производятся в конце периодов (в конце года, квартала, месяца);

· ренту пренумерандо, когда платежи производятся в начале периодов (в начале года, квартала, месяца).