Поперечная цилиндрическая проекция
Поперечная цилиндрическая проекция применяется для составления морских навигационных карт и карт-сеток на приполюсные районы для j Г > 75¸80°N(S).
Как и нормальная цилиндрическая проекция Меркатора (см. п. 6.2), эта проекция является равноугольной (не искажает углы).
При построении и использовании карт в данной проекции применяется система квазигеографических координат («квази» (лат.) – как бы»), которая получается следующим образом (рис. 10.1):
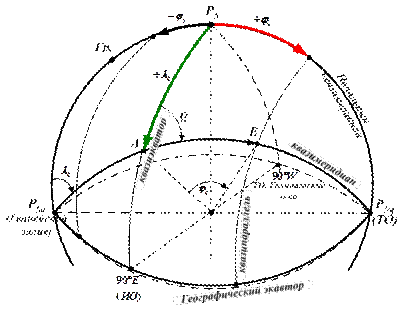
Рис. 10.1. Поперечная цилиндрическая проекция
† Северный полюс условно помещается в точку с координатами: jГ = 0°, lГ = 180° (р-н Тихого океана), а южный полюс – в точку с координатами: jГ = 0°, lГ = 0° (р-н Гвинейского залива).
Полученные точки называются квазиполюсами: PNq – северным, PSq – южным.
† Проведя квазимеридианы и квазипараллели относительно квазиполюсов, получим новую систему координат, повернутую на 90° относительно географической.
Координатными осями этой системы будут:
1) ® начальный квазимеридиан – большой круг, проходящий через северный географический полюс (PN) и квазиполюсы (PNq и PSq), он совпадает с географическим (lГ = 0° и lГ = 180°) Гринвичским (начальным) меридианом;
2) ® квазиэкватор – большой круг, проходящий через географический полюс (PN) и точки на экваторе с долготами: lГ = 90°Е (р-н Индийского океана) и lГ = 90°W (р-н Галапагоских островов).
Координатными линиями этой системы являются:
1) ® квазимеридианы – большие круги, проходящие через квазиполюсы;
2) ® квазипараллели – малые круги, плоскости которых параллельны плоскости квазиэкватора.
Положение любой точки на поверхности Земли на картах в поперечной цилиндрической проекции определяется квазиширотой (jq) и квазидолготой (lq).
† Квазиширота (jq)® угол при центре Земли (шара) между плоскостью квазиэкватора и радиусом, проведенным в данную точку земной поверхности. Квазиширота определяет положение квазипараллелей; отсчитывается от квазиэкватора к квазиполюсам: к PNq ® +jq и к PSq ® –jq от 0° до 90°.
† Квазидолгота (lq) ®двугранный угол при квазиполюсе между плоскостями начального квазимеридиана и квазимеридиана данной точки. Квазидолгота определяет положение квазимеридианов; отсчитывается от географического полюса РN по квазиэкватору к востоку (+lq) и к западу (–lq) от 0° до 180°.
Началом отсчета квазигеографических координат является географический северный полюс (т. РN).
Основные уравнения поперечной цилиндрической равноугольной проекции имеют вид:
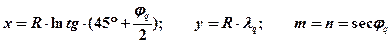 (10.1)
(10.1)
где 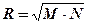 (10.2)
(10.2)
– радиус Земли (м);
m и n – частные масштабы по квазимеридиану и квазипараллели.
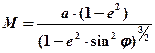 (10.3)
(10.3)
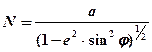 (10.4)
(10.4)
где а = 3437,74¢.
Для эллипсоида Красовского: а = 6378245 м.
Переход от географических координат к квазикоординатам выполняется по формулам:
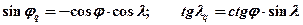 (10.5)
(10.5)
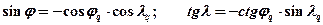 (10.6)
(10.6)
Прямой линией на такой карте изображается квазилоксодромия, пересекающая квазимеридианы под одним и тем же квазикурсом Кq (рис. 10.2).
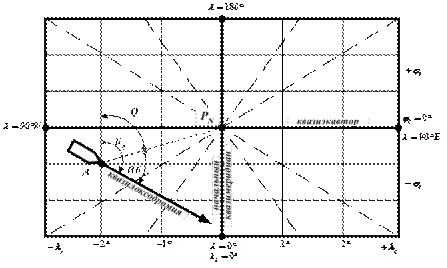
Рис. 10.2. Квазилоксодромия
Локсодромия, вследствие кривизны географических меридианов, сходящихся на полюсе, будет изображаться кривой линией, обращенной выпуклостью к экватору.
Ортодромия же представит собой кривую малой кривизны, обращенную выпуклостью в сторону ближайшего квазиполюса.
Таким образом, при построении квазигеографической сетки карты используются формулы, аналогичные формулам для нормальной проекции Меркатора с заменой в них географических координат квазигеографическими.
Главный масштаб карт и карт-сеток относят к квазиэкватору.
Географические меридианы изображаются кривыми, близкими к прямым линиям.
Географические параллели изображаются кривыми линиями, близкими к окружностям.
Квазикурс (Кq) – угол между квазисеверной частью квазимеридиана и направлением носовой части продольной оси судна (отсчитывается по часовой стрелке от 0° до 360°).
Для перехода от географических направлений к направлениям в квазигеографической системе координат используется угол перехода Q – угол между географическим меридианом и квазимеридианом, значение которого можно получить из треугольника АPNPNq (рис. 10.1).
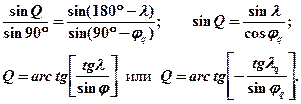 (10.7)
(10.7)
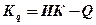 (10.8)
(10.8)
В широтах >80°, когда соs jq » 1, получим:
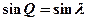 (10.9)
(10.9)
т.е. в высоких широтах угол перехода практически равен долготе точки (Q » 1).
Прокладка курса на такой карте относительно географических или квазигеографических меридианов осуществляется по формуле:
 (10.10)
(10.10)
Для прокладки расстояний необходимо пользоваться специальными вертикальными шкалами с линейным масштабом в морских милях, находящимися за боковыми рамками карт.
Для приполюсных районов Северного Ледовитого океана (СЛО) издаются карты М 1:500.000, на которых красным цветом нанесены квазипараллели, а черным цветом – географические меридианы и параллели с двойной оцифровкой красным и зеленым цветом. Это позволяет использовать карту-сетку в двух районах, симметричных относительно географических меридианов 0°…..180° и 90°Е…..90°W.
По аналогии с нормальной проекцией Меркатора на картах и картах-сетках в поперечной проекции Меркатора прямой линией изображается квазилоксодромия – кривая на поверхности Земли, пересекающая квазимеридианы под постоянным углом Кq (при jq £ 15° ее можно принимать за кратчайшую линию).
Уравнение квазилоксодромии:
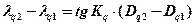 (10.11)
(10.11)
где lq2 – lq1 – разность квазидолгот точек;
Dq2 – Dq1 – разность квазимеридиональных частей (табл. 26 «МТ-75» или табл. 2.28а «МТ-2000»).
Уравнение (10.11) используется при аналитическом счислении в квазигеографической системе координат.
Если известен главный масштаб карты или карты-сетки
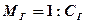 (10.12)
(10.12)
по квазиэкватору, то частный масштаб
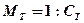 (10.13)
(10.13)
в точке с квазиширотой jq вычисляется по формуле:
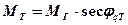 (10.14)
(10.14)
или 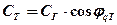 (10.15)
(10.15)
(масштаб карт увеличивается по мере удаления от квазиэкватора).
Дата добавления: 2017-09-01; просмотров: 2495;











