ЦАП с суммированием напряжений

Схема восьмиразрядного преобразователя с суммированием напряжений, изготавливаемого в виде ИМС, приведена на рис. 8.12. Основу преобразователя составляет цепь из 256 резисторов равного сопротивления, соединенных последовательно. Вывод W через ключи S0…S255 может подключаться к любой точке этой цепи в зависимости от входного числа. Входной двоичный код D преобразуется дешифратором 8х256 в унитарный позиционный код, непосредственно управляющий ключами. Если приложить напряжение U_AB между выводами А и В, то напряжение между выводами W и B составит

U_WB=U_ABD.

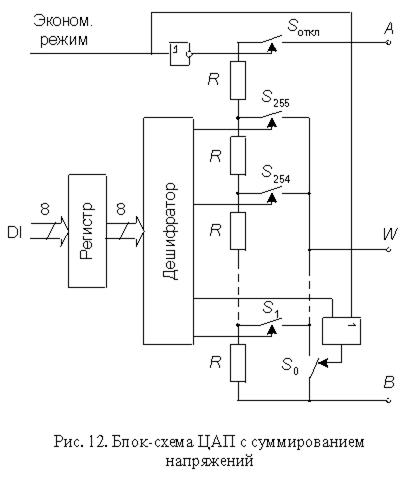
Рисунок 5.10. Блок схема ЦАП с суммированием напряжений

Достоинством данной схемы является малая дифференциальная нелинейность и гарантированная монотонность характеристики преобразования. Ее можно использовать в качестве резистора, подстраиваемого цифровым кодом. Выпускается несколько моделей таких ЦАП. Например, микросхема AD8403 содержит четыре восьмиразрядных ЦАП, выполненных по схеме на рис. 8.12, с сопротивлением между выводами А и В 10, 50 либо 100 кОм в зависимости от модификации. При подаче активного уровня на вход “Экономичный режим” происходит размыкание ключа Sоткл и замыкание ключа S0. ИМС имеет вход сброса, которым ЦАП можно установить на середину шкалы. Фирма Dallas Semiconductor выпускает несколько моделей ЦАП (например, сдвоенный DS1867) с суммированием напряжений, у которых входной регистр представляет собой энергонезависимое оперативное запоминающее устройство, что особенно удобно для построения схем с автоматической подстройкой (калибровкой). Недостаток схемы – необходимость изготавливать на кристалле большое количество (2N) согласованных резисторов. Тем не менее, в настоящее время выпускаются 8-ми, 10-ти и 12-ти разрядные ЦАП данного типа с буферными усилителями на выходе, например, AD5301, AD5311 и AD5321.

Параметры ЦАП

При последовательном возрастании значений входного цифрового сигнала D(t) от 0 до 2N-1 через единицу младшего разряда (ЕМР) выходной сигнал U_вых(t) образует ступенчатую кривую. Такую зависимость называют обычно характеристикой преобразования ЦАП. В отсутствие аппаратных погрешностей средние точки ступенек расположены на идеальной прямой 1 (рис. 22), которой соответствует идеальная характеристика преобразования. Реальная характеристика преобразования может существенно отличаться от идеальной размерами и формой ступенек, а также расположением на плоскости координат. Для количественного описания этих различий существует целый ряд параметров.

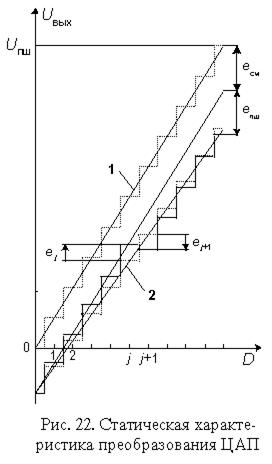
Рисунок 5.11. Статическая характеристика преобразования ЦАП