Представление отрицательных чисел в двоичной системе счисления
Положительные числа нами были рассмотрены ранее. Рассмотрим способы представления отрицательных чисел в двоичном коде. Существует несколько способов такого представления. Мы рассмотрим три:
1. прямой код (в этом случае в двоичном числе выделяется бит-знака - старший бит). Рассмотрим однобайтное (8 бит) двоичное число со знаком.
Старший бит младший бит
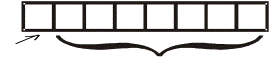
бит-знакa мантисса
Рисунок 2.5 - Представление однобайтных чисел со знаком
Если бит-знак равен 0, то число считается положительным, а если бит-знак равен 1 = отрицательным.
Например, 1210=000011002
-1210=100011002
Недостатком прямого кода является невозможность выполнения арифметических операций.
Рассмотрим сложение: 12+(-12)=0
+10001100
10011000 (-24)
Как видим в результате сложения получились число -24, что не равно 0.
2. смещенный код (аналогично прямому коду двоичное число, в смещенном число разделяется на бит-знак и мантиссу, причем, если бит-знак равен 0, то это число отрицательное, а если бит-знак равен 1 - положительное).
Числа здесь представляются так:
Таблица 2.1
| Число в смещенном коде | Двоичный код | Число без знака |
| ………. | ……… | ..……. |
| -1 | ||
| ………. | ………. | ……… |
| -127 | ||
| -128 |
Достоинством данной системы является то, что в ней выполняются арифметические операции, правда с учетом коррекции результата. А недостатком является то, что 0 соответствует числу 128.
Рассмотрим сложение: 12+(-12)=0
+01110100
100000000 (0)
Как видим, в результате операции получилось число 256. Ограничив предел рассмотрения одним байтом, получим 00000000, к этому результату надо прибавить смещение 128.
Рассмотрим сложение: 12+(-13)=0
+01110011
11111111 (-1)
Как видим, и в данном случае к результату необходимо прибавить 128 и ограничить рассмотрение одним байтом.
3. дополнительный код (это наиболее широко используемый код для представления отрицательных чисел). В нем в числе также выделяется бит-знак в старшем разряде. В дополнительном коде ноль в старшем разряде соответствует положительным числам, а единица - отрицательным числам, но при этом положительные числа представляются как обычно, а отрицательные - в виде записи дополнительного кода.
Рассмотрим порядок перевода числа -9 из десятичной системы в дополнительный код:
1. запишем число без знака: 9;
2. преобразуем число в двоичный код: 00001001;
3. получим обратный код: 11110110;
4. прибавим 00000001 и получим: 11110111.
Если результат операции представлен в дополнительном коде, то для перевода его в десятичный вид используем нижеследующую процедуру
1. запишем дополнительный код: 11110111;
2. получим обратный код: 00001000;
3. прибавим 00000001: 00001001;
4. преобразуем число в десятичный код: -9
Знак минус мы добавили, так как знаем, что наше исходное число в дополнительном коде отрицательное (старший бит равен 1)
Рассмотрим таблицу соответствия чисел представленных в дополнительном коде.
Таблица 2.2
| Число со знаком | Двоичный код | Число без знака |
| +127 | ||
| ………………………. | ………………………… | ………………………… |
| +2 | ||
| +1 | ||
| +0 | ||
| -1 | ||
| -2 | ||
| -3 | ||
| ………………………. | ………………………… | ………………………… |
| -128 |
В дополнительном коде сохраняются все правила выполнения арифметических операций.
Дата добавления: 2021-09-07; просмотров: 782;











