Движение заряженной частицы в однородном электромагнитном поле
Рассмотрим движение малой частицы с массой 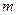 и электрическим зарядом
и электрическим зарядом 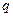 в стационарном однородном электромагнитном поле с напряжённостью электрического поля
в стационарном однородном электромагнитном поле с напряжённостью электрического поля 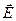 и индукцией магнитного поля
и индукцией магнитного поля 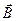 . Вектор напряжённости электрического поля
. Вектор напряжённости электрического поля 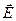 можно разложить на составляющую, параллельную индукции магнитного поля, и перпендикулярную к ней:
можно разложить на составляющую, параллельную индукции магнитного поля, и перпендикулярную к ней:
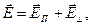
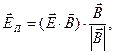
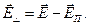 (1)
(1)
Декартову систему координат для рассматриваемого случая удобно выбрать следующим образом: ось 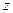 направим вдоль вектора индукции магнитного поля, ось
направим вдоль вектора индукции магнитного поля, ось 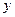 направим вдоль составляющей напряженности электрического поля
направим вдоль составляющей напряженности электрического поля 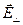 , а направление оси
, а направление оси 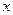 выберем так, чтобы система координат была «правой». В этой системе координат векторы
выберем так, чтобы система координат была «правой». В этой системе координат векторы 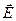 и
и 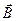 имеют проекции:
имеют проекции:
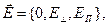
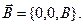 (2)
(2)
Уравнения движения заряженной частицы под действием силы Лоренца запишем в виде:
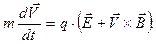 (3)
(3)
В проекциях на соответствующие оси координат уравнение (3) переходит в систему уравнений:
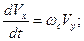
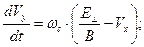
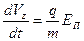 ;
; 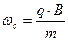 . (4)
. (4)
Параметр движения 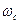 - циклотронная частота. Система уравнений (4) имеет решение:
- циклотронная частота. Система уравнений (4) имеет решение:
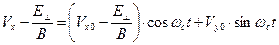 , (5)
, (5)
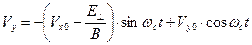 , (6)
, (6)
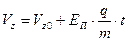 . (7)
. (7)
В приведённых зависимостях величины 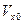 ,
, 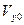 и
и 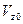 представляют собой проекции вектора скорости частицы в начальный момент времени на соответствующие направления координатных осей. Интегрированием выражений (5)-(7) по времени с учётом начального положения частицы в пространстве получаем зависимости для текущих координат заряженной частицы:
представляют собой проекции вектора скорости частицы в начальный момент времени на соответствующие направления координатных осей. Интегрированием выражений (5)-(7) по времени с учётом начального положения частицы в пространстве получаем зависимости для текущих координат заряженной частицы:
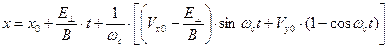 , (8)
, (8)

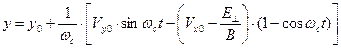 , (9)
, (9)
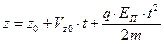 . (10)
. (10)
Анализируя системы соотношений (4), (5)-(7) и (8)-(10), отметим, что продольное движение заряженной частицы осуществляется независимо от поперечного движения и является равнопеременным во времени, такое движение рассматривалось в элементарном курсе физики. Уравнения (5)-(6) поперечного по отношению к вектору индукции магнитного поля движения заряженной частицы позволяют проверить, что модуль поперечной скорости частицы остаётся постоянным с течением времени в системе координат 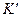 , которая движется вдоль оси
, которая движется вдоль оси 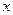 со скоростью
со скоростью 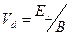 :
:
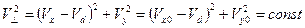 . (11)
. (11)
Скорость системы координат 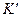 называют скоростью электрического дрейфа заряженной частицы в магнитном поле. Переход в эту систему координат позволяет рассматривать движение заряженной частицы так, как будто бы поперечного электрического поля просто не существует.
называют скоростью электрического дрейфа заряженной частицы в магнитном поле. Переход в эту систему координат позволяет рассматривать движение заряженной частицы так, как будто бы поперечного электрического поля просто не существует.
Полученный результат справедлив и в общем случае. Пусть 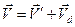 , где
, где 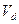 -постоянный (пока неопределённый) вектор, и справедливо уравнение (3):
-постоянный (пока неопределённый) вектор, и справедливо уравнение (3):
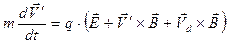 . (12)
. (12)
Потребуем, чтобы выполнялось условие:
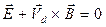 . (13)
. (13)
Умножим каждое слагаемое левой части уравнения (13) векторно на 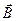 и используем известные тождества векторной алгебры:
и используем известные тождества векторной алгебры:
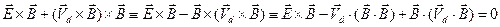 . (14)
. (14)
Одно из решений уравнения (14) можно записать в виде:
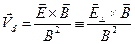 . (15)
. (15)
Общее решение уравнения (14) имеет вид
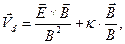
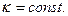 (16)
(16)
Добавка произвольной скорости в продольном направлении никак не сказывается на поперечном движении заряженной частицы, поэтому для определения скорости электрического дрейфа обычно пользуются зависимостью (15).
Уравнения поперечного движения заряженной частицы можно привести к безразмерному виду:
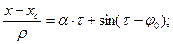
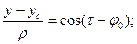
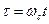 ;
; 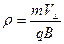 , (17)
, (17)
где
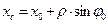 ,
, 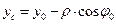 ,
, 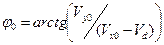 ,
, 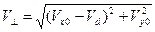 . (18)
. (18)
Параметр 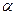 в первом из соотношений (17) представляет собой отношение
в первом из соотношений (17) представляет собой отношение
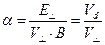 (19)
(19)
и определяет форму траектории заряженной частицы в проекции на плоскость 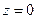 : при
: при 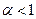 имеем удлинённую циклоиду, при
имеем удлинённую циклоиду, при 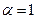 - циклоиду, а при
- циклоиду, а при 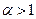 - укороченную циклоиду (или трохоиду).
- укороченную циклоиду (или трохоиду).
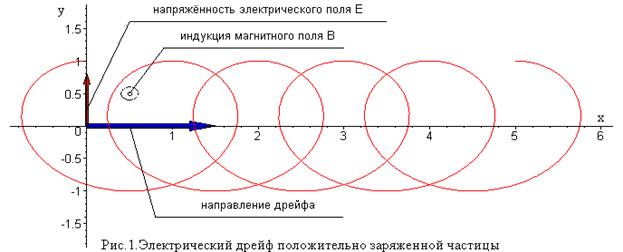
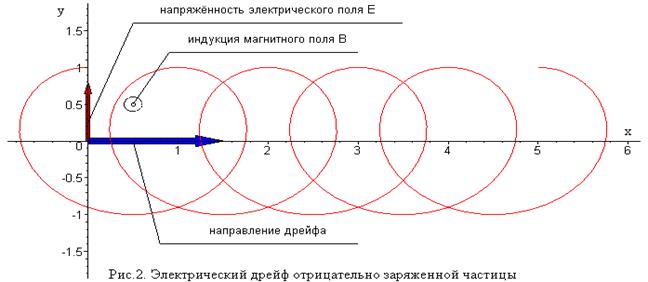
На рисунках 1 и 2 показано различие траекторий положительно и отрицательно заряженных частиц в скрещенных электрическом и магнитном однородных полях в отсутствие продольной скорости частицы. Расчёты траекторий выполнены для 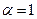 и для специально выбранных значений начальных поперечных координат и начальных проекций поперечной скорости заряженных частиц. Здесь важно заметить, что направление электрического дрейфа перпендикулярно вектору индукции магнитного поля и вектору поперечного электрического поля и не зависит от знака электрического заряда частицы (в зависимости от знака электрического заряда частицы меняется направление «вращения»). В однородном электромагнитном поле движение заряженных частиц в форме дрейфа происходит с постоянной скоростью «ведущего центра», так называют точку плоскости, вокруг которой имеет место мгновенное вращение заряженной частицы.
и для специально выбранных значений начальных поперечных координат и начальных проекций поперечной скорости заряженных частиц. Здесь важно заметить, что направление электрического дрейфа перпендикулярно вектору индукции магнитного поля и вектору поперечного электрического поля и не зависит от знака электрического заряда частицы (в зависимости от знака электрического заряда частицы меняется направление «вращения»). В однородном электромагнитном поле движение заряженных частиц в форме дрейфа происходит с постоянной скоростью «ведущего центра», так называют точку плоскости, вокруг которой имеет место мгновенное вращение заряженной частицы.
| <== предыдущая лекция | | | следующая лекция ==> |
| Электронный осциллограф. | | | Движение частицы в однородном магнитном поле. |
Дата добавления: 2017-09-01; просмотров: 2913;











