Намагничивание парамагнетиков и поляризация диэлектриков внешним полем. Теория Ланжевена-Дебая.
В предыдущих разделах показано, что электрический диполь с моментом 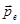 в электрическом поле с напряженностью
в электрическом поле с напряженностью 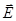 и магнитный диполь с моментом
и магнитный диполь с моментом 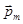 в магнитном поле с индукцией
в магнитном поле с индукцией 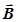 ведут себя удивительно одинаково. Это дает нам возможность рассмотреть явление поляризации диэлектриков в электрическом поле и намагничивание парамагнетиков в магнитном поле с единых позиций. Более того, почти простой заменой обозначений в получаемых ниже формулах можно перейти от одного случая к другому. Для определенности будем делать выкладки для случая намагничивания, тем более что исторически рассматриваемая ниже теоретическая модель намагничивания парамагнетиков была построена П.Ланжевеном (1872-1946) на несколько лет раньше аналогичной модели П.Дебая (1884-1966) для диэлектриков, состоящих из жестких электрических диполей.
ведут себя удивительно одинаково. Это дает нам возможность рассмотреть явление поляризации диэлектриков в электрическом поле и намагничивание парамагнетиков в магнитном поле с единых позиций. Более того, почти простой заменой обозначений в получаемых ниже формулах можно перейти от одного случая к другому. Для определенности будем делать выкладки для случая намагничивания, тем более что исторически рассматриваемая ниже теоретическая модель намагничивания парамагнетиков была построена П.Ланжевеном (1872-1946) на несколько лет раньше аналогичной модели П.Дебая (1884-1966) для диэлектриков, состоящих из жестких электрических диполей.
Рассмотрим безграничную однородную среду, заполненную магнитными диполями с магнитными моментами 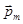 (т.е. элементарными контурами с током по гипотезе Ампера). Допустим, что модуль величины
(т.е. элементарными контурами с током по гипотезе Ампера). Допустим, что модуль величины 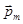 не может измениться (
не может измениться ( 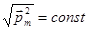 ). Допустим, что объемная концентрация магнитных диполей равна n. В физически бесконечно малом объеме пространства dV содержится
). Допустим, что объемная концентрация магнитных диполей равна n. В физически бесконечно малом объеме пространства dV содержится 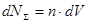 магнитных диполей. Полагаем, что объемная концентрация магнитных диполей достаточно мала, чтобы можно было пренебречь влиянием диполей друг на друга. Полагаем также, что под действием температуры в отсутствие внешнего силового поля распределение по направлению магнитных диполей
магнитных диполей. Полагаем, что объемная концентрация магнитных диполей достаточно мала, чтобы можно было пренебречь влиянием диполей друг на друга. Полагаем также, что под действием температуры в отсутствие внешнего силового поля распределение по направлению магнитных диполей 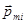 , i - номер диполя, входящего в объем dV, является хаотичным. Интуитивный физический смысл этого утверждения очевиден. Облечем его в строгую математическую форму. Пусть элемент объема dV, а значит совокупность магнитных диполей
, i - номер диполя, входящего в объем dV, является хаотичным. Интуитивный физический смысл этого утверждения очевиден. Облечем его в строгую математическую форму. Пусть элемент объема dV, а значит совокупность магнитных диполей 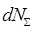 , находится в начале сферической системы координат
, находится в начале сферической системы координат 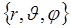 . Элемент площади поверхности сферы, описываемой уравнением
. Элемент площади поверхности сферы, описываемой уравнением 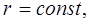 имеет вид:
имеет вид: 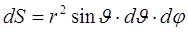 . Телесный угол, в пределах которого описанный элемент площади виден из начала координат, имеет вид:
. Телесный угол, в пределах которого описанный элемент площади виден из начала координат, имеет вид:
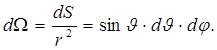 (1)
(1)
Будем считать, что распределение дипольных магнитных моментов в элементе объема хаотично, если выполнено условие:
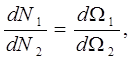 (2)
(2)
где 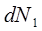 – число магнитных диполей с магнитным моментом с ориентацией внутри элемента телесного угла
– число магнитных диполей с магнитным моментом с ориентацией внутри элемента телесного угла 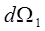 ,
, 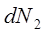 - число магнитных диполей с магнитным моментом с ориентацией внутри элемента телесного угла
- число магнитных диполей с магнитным моментом с ориентацией внутри элемента телесного угла 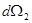 .
.
Смысл определения (2) сводится к посылке: чем больше рассматриваемый телесный угол, тем большее число магнитных диполей обладают магнитными моментами, направление которых может варьироваться в пределах этого угла.
Замкнутая (полная) сфера видна из центра сферы под углом 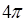 стерадиан, а полное число рассматриваемых частиц при этом
стерадиан, а полное число рассматриваемых частиц при этом 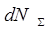 . С учетом сказанного из соотношения (2) можно получить:
. С учетом сказанного из соотношения (2) можно получить:
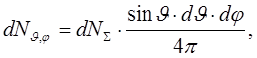 (3)
(3)
где 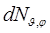 – число дипольных магнитных моментов, направление которых определено угловыми переменными в пределах от
– число дипольных магнитных моментов, направление которых определено угловыми переменными в пределах от 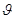 до
до 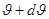 и от
и от 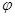 до
до 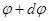 .
.
Ниже нас будут интересовать физические ситуации с осевой симметрией. В этих условиях соотношение (3) можно проинтегрировать по переменной 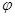 в пределах от значения
в пределах от значения  до значения
до значения 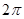 :
:
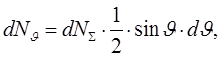 (4)
(4)
Напомним, что здесь 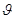 – угол между осью z и радиус-вектором точки поверхности сферы.
– угол между осью z и радиус-вектором точки поверхности сферы.
Если pm – модуль магнитного момента отдельной частицы, 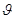 - значение описанного выше угла, то проекция вектора
- значение описанного выше угла, то проекция вектора 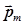 на направление z имеет вид
на направление z имеет вид 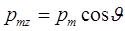 . По правилу вычисления средней величины получим с учётом соотношения (4):
. По правилу вычисления средней величины получим с учётом соотношения (4):
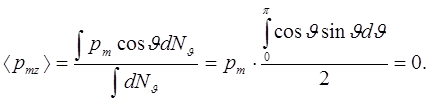 (5)
(5)
Направление оси z можно выбрать произвольно, поэтому можно сказать, что для любого направления величина 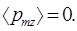 Поскольку проекция намагниченности среды
Поскольку проекция намагниченности среды 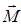 на ось z определяется соотношением
на ось z определяется соотношением
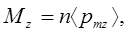 (6)
(6)
то из соотношения (5) следует, что хаотическое распределение векторов магнитных моментов в элементе объема dV по направлению в пространстве не приводит к намагничиванию среды.
Теперь допустим, что ось z выбрана по направлению внешнего магнитного поля 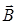 . Теперь каждый магнитный диполь испытывает со стороны внешнего магнитного поля воздействие, результатом которого является уменьшение угла между направлением магнитного момента диполя
. Теперь каждый магнитный диполь испытывает со стороны внешнего магнитного поля воздействие, результатом которого является уменьшение угла между направлением магнитного момента диполя 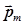 и направлением магнитной индукции
и направлением магнитной индукции 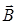 . Энергетической мерой этого воздействия является величина потенциальной энергии магнитного диполя во внешнем магнитном поле с магнитной индукцией
. Энергетической мерой этого воздействия является величина потенциальной энергии магнитного диполя во внешнем магнитном поле с магнитной индукцией 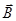 :
:
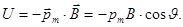 (7)
(7)
Тепловое движение системы магнитных диполей направлено на усиление хаотичности распределения магнитных диполей по направлению. Энергетической мерой теплового воздействия является величина kT, где k– коэффициент Больцмана, Т – абсолютная температура среды.
В рассматриваемой ситуации вместо условия (2) в соответствии с принципом Больцмана должно иметь место соотношение:
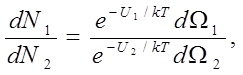 (8)
(8)
где U1 , U2 – значения потенциальной функции системы в первом и во втором состоянии соответственно.
Из соотношения (8) следует:
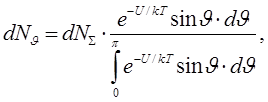 (9)
(9)
Соотношение (9) получено с использованием очевидной нормировки:
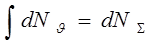 . (10)
. (10)
Вычисление величины 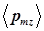 с учетом соотношения (9) приводит к выражению:
с учетом соотношения (9) приводит к выражению:
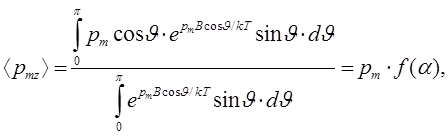 (11)
(11)
где
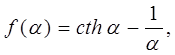
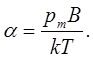 (12)
(12)
Здесь 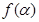 – функция Ланжевена, график которой показан на рис. 1.
– функция Ланжевена, график которой показан на рис. 1.
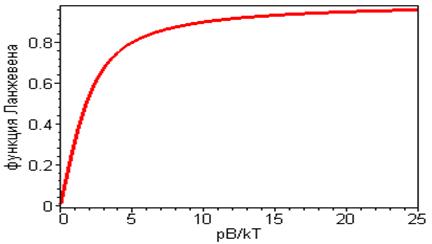

Легко проверить, что при малых значениях параметра 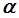 (малые значения индукции внешнего поля, или большие значения температуры среды)
(малые значения индукции внешнего поля, или большие значения температуры среды)
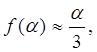
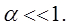 (13)
(13)
При больших значениях параметра 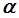 имеем:
имеем:
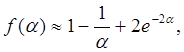
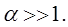 (14)
(14)
Проекция 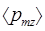 по выражению (11) является единственной отличной от нуля проекцией вектора
по выражению (11) является единственной отличной от нуля проекцией вектора 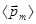 на направление индукции магнитного поля
на направление индукции магнитного поля 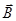 . Ориентация осреднённого вектора
. Ориентация осреднённого вектора 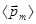 совпадает с ориентацией вектора магнитной индукции внешнего магнитного поля
совпадает с ориентацией вектора магнитной индукции внешнего магнитного поля 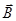 . Суммарный магнитный момент элемента объема dV определен выражением:
. Суммарный магнитный момент элемента объема dV определен выражением:
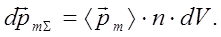 (15)
(15)
В этом случае вектор намагниченности принимает вид:
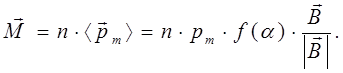 (16)
(16)
Традиционно вектор намагниченности 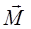 считают функцией вектора напряженности внешнего магнитного поля
считают функцией вектора напряженности внешнего магнитного поля 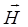 . В этом случае:
. В этом случае:
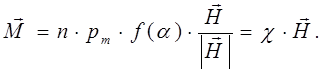 (17)
(17)
где 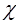 – магнитная восприимчивость среды. Для величины
– магнитная восприимчивость среды. Для величины 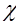 можно получить:
можно получить:
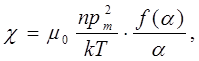
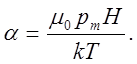 (18)
(18)
Соотношение (18) позволяет вычислить зависимость магнитной проницаемости парамагнитной среды от величины напряжённости внешнего магнитного поля: 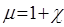 .
.
Заметим, что зависимость 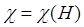 в общем случае не линейна. Для малых значений параметра
в общем случае не линейна. Для малых значений параметра 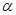 (формула (13)) имеем:
(формула (13)) имеем:
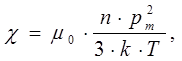 (19)
(19)
что можно записать в форме закона Кюри:
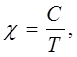
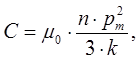 (20)
(20)
где С - постоянная Кюри.
Легко видеть, что магнитная восприимчивость среды определяется объемной концентрацией диполей, величиной их магнитного момента и абсолютной температурой. В “сильных” магнитных полях (или при “низких” температурах) величина 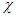 нелинейным образом зависит от безразмерного параметра
нелинейным образом зависит от безразмерного параметра 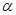 , т.е. от величины напряженности магнитного поля.
, т.е. от величины напряженности магнитного поля.
Формула (17) удачно описывает явление насыщения. Вектор 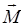 остается ограниченным по величине при бесконечно большом увеличении индукции внешнего магнитного поля
остается ограниченным по величине при бесконечно большом увеличении индукции внешнего магнитного поля 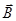 , или напряженности магнитного поля
, или напряженности магнитного поля 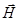 .
.
Для вектора поляризованности среды 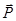 , очевидно, можно получить:
, очевидно, можно получить:
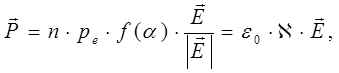 (21)
(21)
где 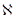 – диэлектрическая восприимчивость среды:
– диэлектрическая восприимчивость среды:
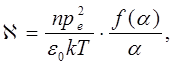
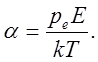 (22)
(22)
со всеми вытекающими последствиями. В частности, соотношение (22) позволяет вычислить величину диэлектрической проницаемости среды при наличии внешнего электрического поля напряжённости 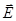 :
: 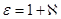 . Заметим, что соотношение (22) справедливо для среды электрических диполей, для которых
. Заметим, что соотношение (22) справедливо для среды электрических диполей, для которых 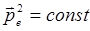 : случай “атомной” поляризации здесь не рассматривается.
: случай “атомной” поляризации здесь не рассматривается.
В проведенном выше анализе было принято, что отдельные диполи в рассматриваемом физически бесконечно малом объеме не взаимодействуют между собой. В общем случае это взаимодействие имеет место и сводится к появлению в среде “собственного” поля, которое накладывается на “внешнее” поле. Последнее обстоятельство принуждает нас рассматривать поведение отдельного диполя, электрического или магнитного, в некотором “эффективном” поле.
Существуют методы расчета упомянутого эффективного поля, в частности, метод “самосогласованного” поля Хартри-Фока, и метод пробной частицы. Обсуждение этих методов является предметом специального исследования.
Ниже рассмотрим одну простую модель среды с учетом взаимодействия диполей между собой. Положим, что “собственное” магнитное поле как результат взаимного влияния диполей друг на друга пропорционально величине намагниченности среды
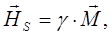 (23)
(23)
где 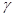 - некоторая безразмерная постоянная, не зависящая от намагниченности
- некоторая безразмерная постоянная, не зависящая от намагниченности 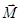 величина. Ее численное значение по оценке Лоренца равно
величина. Ее численное значение по оценке Лоренца равно 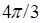 . Экспериментальные значения для разных материалов различны и могут достигать очень больших значений (заметим, что в случае электрического поля размерность величины
. Экспериментальные значения для разных материалов различны и могут достигать очень больших значений (заметим, что в случае электрического поля размерность величины 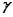 в системе единиц СИ совпадает с размерностью величины
в системе единиц СИ совпадает с размерностью величины 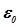 , т.е. Ф×м-1). Более детальный анализ должен был бы учитывать то обстоятельство, что величины
, т.е. Ф×м-1). Более детальный анализ должен был бы учитывать то обстоятельство, что величины 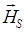 и
и 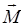 не обязательно должны совпадать по направлению, в этом случае величина
не обязательно должны совпадать по направлению, в этом случае величина 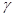 в зависимости (23) являлась бы тензором второго ранга. Ниже величину
в зависимости (23) являлась бы тензором второго ранга. Ниже величину 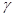 будем считать скалярной величиной.
будем считать скалярной величиной.
Проведенные выше выкладки по расчету величины 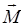 , очевидно, остаются справедливыми при переходе от внешнего поля
, очевидно, остаются справедливыми при переходе от внешнего поля 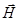 к эффективному полю
к эффективному полю 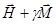 . Соотношение (17) при этом можно переписать в виде формулы Ланжевена-Вейсса:
. Соотношение (17) при этом можно переписать в виде формулы Ланжевена-Вейсса:
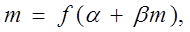
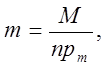
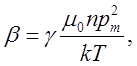 (24)
(24)
где m - безразмерная величина намагниченности среды, 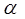 - безразмерный параметр, определенный соотношением (18),
- безразмерный параметр, определенный соотношением (18), 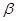 - безразмерный параметр, пропорциональный величине
- безразмерный параметр, пропорциональный величине 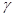 , следовательно, учитывающий влияние “собственного” поля магнитных диполей на эффект намагничивания среды. Интересно отметить, что вместо формулы (17) для расчета величины намагниченности с использованием функции Ланжевена теперь приходится рассматривать уравнение (24) для нахождения величины m, следовательно, и величины намагниченности среды М.
, следовательно, учитывающий влияние “собственного” поля магнитных диполей на эффект намагничивания среды. Интересно отметить, что вместо формулы (17) для расчета величины намагниченности с использованием функции Ланжевена теперь приходится рассматривать уравнение (24) для нахождения величины m, следовательно, и величины намагниченности среды М.
Случай 1. Допустим, что выполняется условие 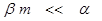 , т.е. HS<<H. В этом случае правую часть соотношения (24) можно разложить в ряд Тейлора в окрестности величины
, т.е. HS<<H. В этом случае правую часть соотношения (24) можно разложить в ряд Тейлора в окрестности величины 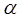 и ограничиться членами нулевого и первого порядка малости:
и ограничиться членами нулевого и первого порядка малости:
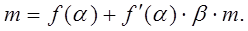 (25)
(25)
Решением полученного уравнения является выражение:
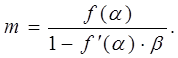 (26)
(26)
Зависимость 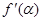 положительно определена для всех
положительно определена для всех 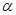 , из выражения (26) получается, что слабое взаимодействие диполей между собой приводит к увеличению намагниченности вещества.
, из выражения (26) получается, что слабое взаимодействие диполей между собой приводит к увеличению намагниченности вещества.
Случай 2. Если выполнено условие 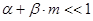 (т.е. и внешнее и собственное магнитные поля “малы”), то можно воспользоваться асимптотическим выражением (13) и получить
(т.е. и внешнее и собственное магнитные поля “малы”), то можно воспользоваться асимптотическим выражением (13) и получить
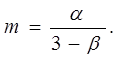 (27)
(27)
Случай 3. Допустим, что внешнее поле в среде отсутствует: 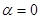 . В этом случае уравнение (24) можно переписать в форме:
. В этом случае уравнение (24) можно переписать в форме:
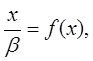
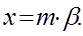 (28)
(28)
Тривиальное решение уравнения (28) х=0 физически возможно, но не очень интересно. Интересно то (Рис.2), что при значениях параметра 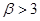 существует отличное от нуля значение переменной х как корня уравнения (28). Последнее соответствует возможности состояния “спонтанной” намагниченности среды. Заметим, что увеличение намагниченности среды приводит к уменьшению потенциальной функции системы магнитных диполей, поэтому состояние с ненулевой намагниченностью предпочтительнее, чем отсутствие таковой. Из этих соображений следует, что состояние m=0 при
существует отличное от нуля значение переменной х как корня уравнения (28). Последнее соответствует возможности состояния “спонтанной” намагниченности среды. Заметим, что увеличение намагниченности среды приводит к уменьшению потенциальной функции системы магнитных диполей, поэтому состояние с ненулевой намагниченностью предпочтительнее, чем отсутствие таковой. Из этих соображений следует, что состояние m=0 при 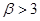 можно было бы рассматривать как метастабильное.
можно было бы рассматривать как метастабильное.
|
|
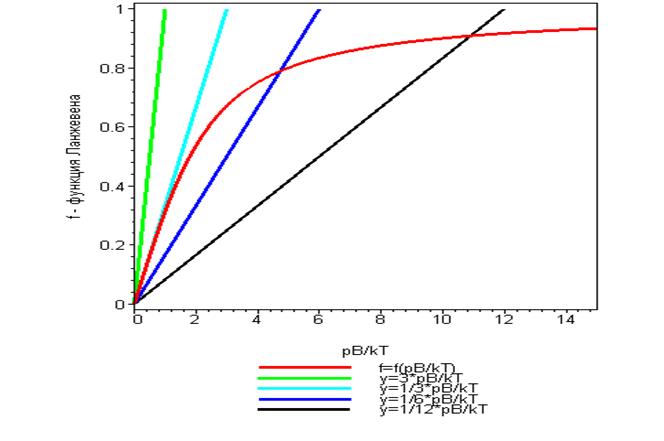
При значениях параметра 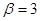 или
или 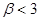 величина намагниченности среды может иметь только нулевое значение (это определяется свойствами функции Ланжевена).
величина намагниченности среды может иметь только нулевое значение (это определяется свойствами функции Ланжевена).
|
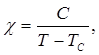
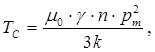 (29)
(29)
где С – постоянная Кюри (соотношение (20)), ТС – температура “точка Кюри”, то приходим к формуле закона Кюри-Вейсса. Спонтанная намагниченность среды может существовать только при температуре, меньшей, чем точка Кюри. Экспериментальное значение точки Кюри для железа составляет около 1000 К, что соответствует значению 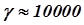 .
.
В заключение настоящего раздела, скажем, что модель Ланжевена (для диэлектриков - модель Дебая) и закон Кюри описывают эффекты намагничивания парамагнетиков, модель Ланжевена-Вейсса и закон Кюри-Вейсса описывают намагничивание ферромагнетиков, антиферромагнетики как среды можно в первом приближении описать как ферромагнетики, у которых температура Кюри (точка Кюри) отрицательна. За более подробным описанием необходимо обратиться к более специальным руководствам.
| <== предыдущая лекция | | | следующая лекция ==> |
| Высокочастотная диэлектрическая проницаемость металлов. | | | Устройство и принцип действия экстракторов |
Дата добавления: 2017-09-01; просмотров: 2603;