Произведение матриц.
Операция произведения определяется не для всех матриц, а лишь для согласованных.
Матрицы А и В называются согласованными, если число столбцов матрицы А равно числу строк матрицы В. Так, если 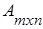 ,
, 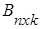 , m≠k, то матрицы А и В согласованные, так как n = n, а в обратном порядке матрицы В и А несогласованные, так как m ≠ k. Квадратные матрицы согласованы, когда у них одинаковый порядок n, причем согласованы как А и В, так и В и А. Если
, m≠k, то матрицы А и В согласованные, так как n = n, а в обратном порядке матрицы В и А несогласованные, так как m ≠ k. Квадратные матрицы согласованы, когда у них одинаковый порядок n, причем согласованы как А и В, так и В и А. Если 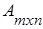 , а
, а 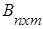 , то будут согласованы матрицы А и В, а также матрицы В и А, так как n = n, m = m.
, то будут согласованы матрицы А и В, а также матрицы В и А, так как n = n, m = m.
Произведением двух согласованных матриц 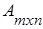 и
и 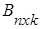
А= 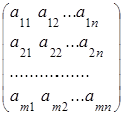 , В=
, В= 
называется матрица С порядка m´k:
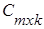 =
= 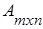 ∙
∙ 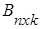 , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:
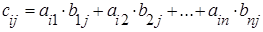 (
( 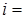 1, 2, 3, …, m , j=1, 2, 3, …, k),
1, 2, 3, …, m , j=1, 2, 3, …, k),
то есть элемент 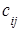 i –ой строки и j –го столбца матрицы С равен сумме произведений всех элементов i –ой строки матрицы А на соответствующие элементы j –го столбца матрицы В.
i –ой строки и j –го столбца матрицы С равен сумме произведений всех элементов i –ой строки матрицы А на соответствующие элементы j –го столбца матрицы В.
Пример.Найти произведение матриц А и В.
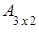 =
= 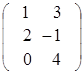 ,
, 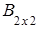 =
= 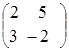 ,
,
 ∙
∙ 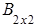 =
= 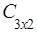 =
= 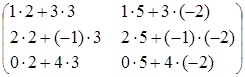 =
= 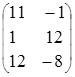 .
.
Произведение матриц В∙А не существует, так как матрицы В и А не согласованы: матрица В имеет порядок 2´2, а матрица А – порядок 3´2.
Для любых квадратных матриц единичная матрица Е является коммутирующей к любой матрице А того же порядка, причем в результате получим ту же матрицу А, то есть АЕ = ЕА = А.
Дата добавления: 2021-09-07; просмотров: 400;











