Работа по перемещению проводника с током в магнитном поле.

Учитывая важность для практических приложений вычисления работы при перемещениях или деформациях замкнутого или разомкнутого контура с током, вычислим эту величину без учета предположения о малой величине замкнутого контура.

Рассмотрим сначала разомкнутый контур с элементом тока 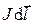. Если в процессе движения элемент 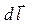контура с током смещается на величину параллельно самому себе, то работа, совершаемая при этом, равна

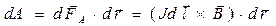. (1)

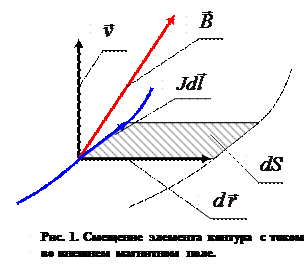Поскольку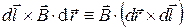

в силу свойств смешанного произведения векторов, а 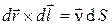, где 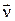- вектор единичной нормали к элементу поверхности 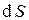, образованного векторам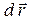и и , то из соотношения (1) получаем:

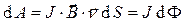, (2)

где 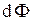- элемент потока вектора 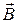через поверхность .

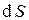Если рассмотреть поворот элемента постоянной длины контура с током 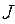на угол 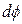в пространстве с магнитным полем, магнитная индукция которого известна, можно убедиться в том, что соотношение (2) остается справедливым.

Поскольку произвольное изменение положения ориентированного элемента кривой состоит из параллельного переноса и поворота, для работы по перемещению в пространстве отрезка контура с током получаем выражение:

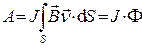. (3)

По выводу зависимости (3) поверхность 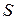построена как поверхность, “ометаемая” отрезком кривой, по которому течет ток, в реальном движении. В силу свойств магнитостатического поля 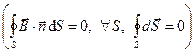в формуле (3) можно использовать любую (произвольную) поверхность, которая опирается на замкнутый контур, состоящий из начального положения отрезка кривой 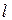, конечного положения отрезка кривой 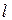и из траектории начальной граничной точки и траектории конечной граничной точки рассматриваемого отрезка.

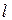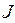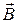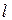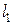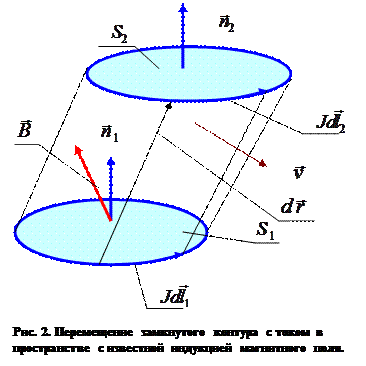
Рассмотрим замкнутый контур , по которому течет ток во внешнем магнитном поле с индукцией . Пусть начальное положение контура описывалось кривой , а конечное - кривой 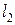(рис. 2). Пусть на контур 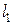натянута поверхность 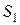, а на контур 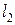натянута поверхность 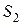, а боковая поверхность “ометаемого” тела построена как поверхность, по которой перемещается элемент 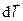из положения 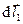в положение .

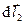С точностью до бесконечно малых второго порядка запишем выражение для работы по перемещению элемента с током 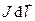из первого положения во второе:

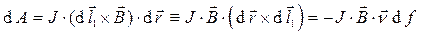, (4)

где 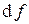- элемент боковой поверхности описанного выше тела, 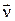- направление внешней нормали к этому элементу. Из теоремы Гаусса в интегральной форме для вектора 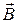легко получить

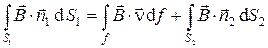. (5)

Из соотношения (5) следует:

. (6)

Соотношение (6) получено без использования предположения о малости контура с током.

Для элементарной работы по перемещению контура с током (J=const) в пространстве получим

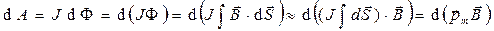. (7)

Подробная последовательность вычислений в формулах (7) проясняет, в каком месте существенно использована посылка о малой величине контура с током при выводе соотношения (10) раздела 7.3..