Что такое Индуктивность.

Электрический ток генерирует в окружающем пространстве магнитное поле. При этом через произвольную поверхность, опирающуюся на необязательно плоский замкнутый контур, можно рассчитать поток вектора магнитной индукции. Поток вектора магнитной индукции зависит от геометрии распределения тока в пространстве, величины силы тока или объёмной плотности тока и геометрии рассматриваемого контура. Для случая, когда электрический ток силы 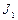течёт по тонкому простому замкнутому контуру 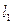, а поток вектора магнитной индукции рассчитывается относительно поверхности, опирающейся на простой замкнутый контур 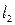, величина потока вектора магнитной индукции прямо пропорциональна величине силы тока 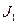. Коэффициент пропорциональности 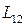называют при этом индуктивностью или коэффициентом взаимной индукции контура 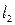в рассматриваемой системе токов (ток течет по контуру 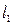). Размерность индуктивности легко вычисляется по приведённому определению, единицей измерения индуктивности является величина 1 Гн («генри»). Ниже в качестве среды будем рассматривать вакуум. Вычислим индуктивность .

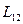В соответствии с законом Био-Савара-Лапласа элемент контура с током 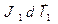порождает в точке наблюдения с радиус-вектором 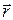элементарный вектор магнитной индукции :

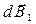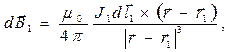(1)

где 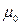- магнитная постоянная, 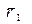- радиус-вектор расположения элемента контура 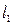с током 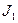, т.е. 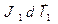. В силу принципа суперпозиции вектор магнитной индукции в точке наблюдения равен:

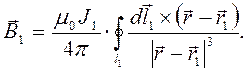(2)

Пусть 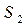- поверхность, опирающаяся на замкнутый контур 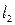, 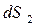- её элемент, 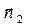- единичный вектор нормали к элементу поверхности 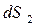, направление которого согласовано с выбором положительного направления обхода контура 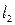, т.е. направления 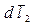. Напомним, что с конца вектора 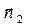направление обхода контура 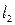положительно, если оно осуществляется в направлении против часовой стрелки. В математической литературе принято говорить, что при обходе контура область изменения переменных должна оставаться слева. Теперь можно вычислить элементарный поток вектора магнитной индукции 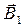через элемент поверхности :

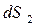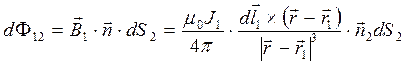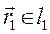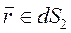, , . (3) Поток 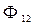вектора магнитной индукции 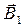через поверхность 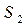определяется квадратурой:

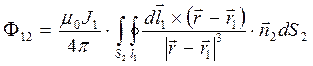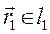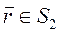, , . (4)

В силу определения

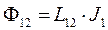(5)

получаем

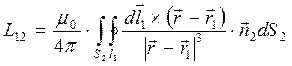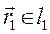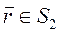, , . (6)

Аналогичным образом можно получить выражение для индуктивности первого контура, если магнитное поле в пространстве определяется током, текущим во втором конуре:

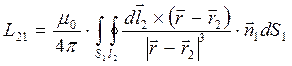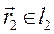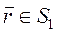, , . (7)

В выражениях (3), (4) и (6) символ 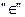- принадлежит – имеет тот смысл, что конец вектора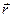

принадлежит соответствующему геометрическому объекту.

Для коэффициентов взаимной индукции (6) и (7) справедлива теорема «взаимности»:

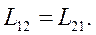(8)

Физический смысл теоремы взаимности определяется соотношением:

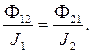(9)

Теорема взаимности для коэффициентов взаимной индукции в форме (8) и (9) далеко не очевидна. Поскольку она важна в теоретических исследованиях и практических приложениях, докажем её справедливость.

Вектор магнитной индукции 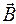связан с векторным потенциалом 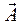стационарного магнитного поля соотношением:

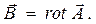(10)

Элементарный поток вектора магнитной индукции 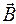через элементарную площадку поверхности 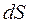с нормалью 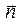можно записать в форме:

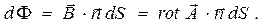(11)

Поток вектора магнитной индукции через поверхность, натянутую на замкнутый контур ,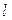

с использованием теоремы Стокса принимает вид:

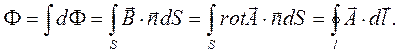(12)

Эквивалентная форма закона Био-Савара-Лапласа имеет вид:

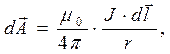(13)

где r – расстояние от элемента с током до точки наблюдения. Векторный потенциал стационарного магнитного поля определяется при этом по принципу суперпозиции:

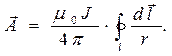(14)

В соотношении (14) ток J течёт по замкнутому контуру .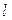

С помощью соотношения (14) легко записывается выражение для векторного потенциала стационарного магнитного поля, образованного током, текущим в первом контуре:

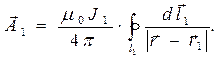(15)

Теперь можно воспользоваться соотношением (12), учитывая, что рассчитывается поток вектора магнитной индукции через поверхность, натянутую на второй контур:

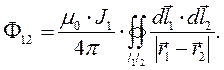(16)

Для коэффициента взаимной индукции второго контура, если магнитное поле образовано током, текущим в первом контуре, получаем выражение:

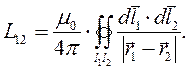(17)

Коэффициент взаимной индукции первого контура, если магнитное поле образовано током, текущим по второму контуру, получается из формулы (17) заменой индексов 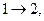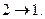Очевидно, что теорема взаимности действительно справедлива.

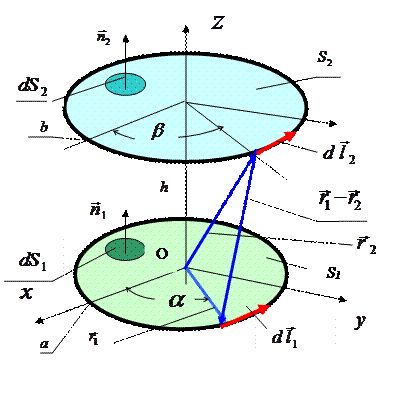
В качестве простого, но не тривиального примера рассчитаем коэффициенты взаимной индукции системы двух плоских тонких круговых колец радиусов 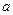и 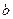, соосно расположенных друг над другом на расстоянии 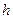параллельно координатной плоскости Oxy декартовой системы координат (рис. 1). Положительными направлениями обхода обоих контуров будем считать движение против часовой стрелки, если смотреть из точки с координатами {0,0,z}, где z>0. Проекции радиусов-векторов расположения элементов первого и второго контуров удобно задать с помощью углов 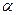и :

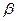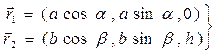(18)

Направленные элементарные отрезки рассматриваемых контуров представлены проекциями:

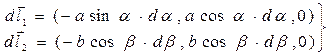(19)

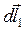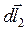Скалярное произведение векторов и определяется выражением:

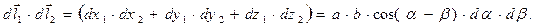(20)

Вычислим расстояние между рассматриваемыми элементарными отрезками первого и второго контуров:

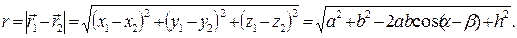(21)

Теперь можно записать выражение для коэффициента взаимной индукции в форме квадратуры:

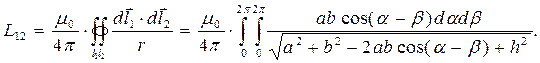(22)

Полученный интеграл не выражается через элементарные функции, результат его вычисления можно записать через полные эллиптические интегралы первого и второго рода:

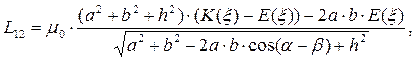(23)

где

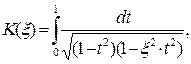
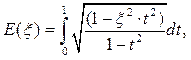
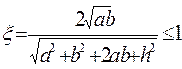(24)

- полные эллиптические интегралы первого и второго рода соответственно и обобщенный параметр задачи. Эллиптические интегралы табулированы во многих справочных математических руководствах, их вычисление включено в большинство математических пакетов для персональных компьютеров, вычисление выражений с эллиптическими интегралами на практике ничуть не сложнее, чем вычисление тригонометрических функций.

Рассмотрим некоторые предельные соотношения, вытекающие из выражения (23). Пусть второй контур системы расположен в плоскости первого контура, при этом параметр :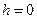

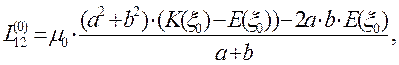(25)

где

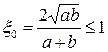. (26)

С помощью пакета символьных вычислений MAPLE получаются результаты:

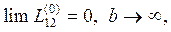
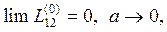
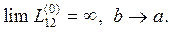(27)

Первые два результата физически очевидны: если второй контур имеет бесконечно большие размеры, то его влиянием можно пренебречь, если размеры первого контура в сравнении с размерами второго контура очень малы, то его тоже можно не учитывать. Получается, что коэффициент взаимной индукции обращается в нуль для одиночного контура. Это естественно: одиночному контуру не с чем взаимодействовать. Что касается третьего предела, то попытка наложить два одинаковых контура друг на друга в рамках рассматриваемого подхода является некорректной. Дело в том, что интеграл

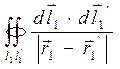
не существует в смысле главного значения: дело «портит» модуль разности векторов в знаменателе подынтегральной функции. Это можно понять, сравнивая два интеграла

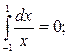
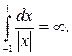
Для расчета коэффициента самоиндукции требуется переходить к модели с распределёнными параметрами и конечными размерами поперечного сечения проводника.