Явление полного внутреннего отражения
Явление полного внутреннего отражения, как правило, рассматривается на основе известных формул Френеля, следующих из основных уравнений классической электродинамики, при условии, что волновые векторы падающей, отражённой и преломлённой волн являются действительными. При полном внутреннем отражении это условие не выполнено, формальное использование формул Френеля с комплексными волновыми векторами приводит к правильным конечным результатам, но в процессе вывода теряется геометрический смысл произведения волнового вектора на комплексное значение косинуса угла преломления как проекции вектора на рассматриваемое направление, что не позволяет считать получаемые результаты обоснованными.
В настоящей работе требуемые результаты получены без использования комплексных значений тригонометрических функций и без нарушений геометрического смысла проведённых вычислений, что полностью обосновывает физико-математическую модель явления.
С теорией явления полного внутреннего отражения плоской гармонической электромагнитной волны на границе раздела двух диэлектриков можно познакомиться по классической монографии Дж.А. Стрэттона [1]. Его результаты основаны на известных представлениях о распространении электромагнитных волн в однородных изотропных средах [2-6]. Заметим, что в работе М. Борна и Э. Вольфа волновой вектор плоской гармонической электромагнитной волны может принимать комплексные значения, но действительная и мнимая составляющие этого вектора принимаются параллельными друг другу [2]. В учебниках теоретической физики Л.Д.Ландау и Е.М.Лифшица по электродинамике сплошных сред в общем случае допускается возможность различных ориентаций в пространстве действительной и мнимой частей волнового вектора [3,4], но при рассмотрении явления полного внутреннего отражения волновой вектор преломлённой волны имеет единственное направление, поскольку его действительная часть обращается в нуль. В учебнике Д.В. Сивухина [5], как и в упомянутых выше источниках, формулы Френеля, полученные для случая «регулярного» явления преломления-отражения плоской гармонической электромагнитной волны на плоской границе раздела двух диэлектриков, формально распространены на случай полного внутреннего отражения. Автором монографии [5], в частности отмечено, что при этом геометрический смысл тригонометрических функций угла преломления теряется: синус угла преломления (закон Снеллиуса) превышает единицу, косинус угла преломления приходится рассматривать как комплексную величину, модуль волнового вектора, умноженный на косинус угла преломления, теряет смысл проекции вектора на направление нормали к поверхности раздела сред, относительный показатель преломления становится комплексной величиной, фазовая скорость распространения электромагнитной волны становится комплексной величиной. Заметим, что последнее обстоятельство не позволяет считать конечные результаты исследования строго обоснованными.
Цель настоящего исследования – провести анализ явления полного внутреннего отражения плоской гармонической электромагнитной волны на границе раздела двух однородных изотропных диэлектриков, не прибегая к использованию комплексных значений тригонометрических функций углов преломления. В этом отношении настоящая работа методологически является продолжением работ авторов [8,9].
Анализ баланса нормальных составляющих плотностей потоков энергии (векторы Умова-Пойнтинга), как правило, проводят для осреднённых по времени действительных величин. При этом оказывается, что нормальная осреднённая компонента вектора Умова-Пойнтинга падающей волны равна по величине нормальной осреднённой компоненте вектора Умова-Пойнтинга отражённой волны, а нормальная осреднённая компонента вектора Умова-Пойнтинга преломлённой волны равна нулю [1-6]. Вместе с этим, преломлённая электромагнитная волна реально существует как неоднородная волна [7].
В настоящей работе помимо анализа баланса нормальных составляющих плотностей потоков энергии (векторы Умова-Пойнтинга) для осреднённых по времени действительных величин проведено исследование баланса нормальных составляющих плотностей потоков энергии (векторы Умова-Пойнтинга для мгновенных действительных величин), что позволило выявить естественный источник существования неоднородной преломлённой электромагнитной волны.
Система уравнений классической электродинамики в диэлектрической (непроводящей) однородной изотропной среде имеет вид:
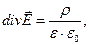
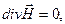
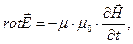
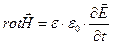 . (1)
. (1)
В уравнениях (1) использованы общепринятые обозначения. Плоская гармоническая волна может быть описана с использованием понятия «комплексная амплитуда»:
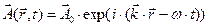 , (2)
, (2)
где 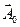 - постоянная комплексная амплитуда,
- постоянная комплексная амплитуда, 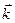 - волновой вектор,
- волновой вектор, 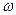 - круговая частота волны,
- круговая частота волны, 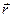 - радиус-вектор точки наблюдения. Ниже круговую частоту принимаем постоянной действительной величиной, а волновой вектор – постоянной, возможно комплексной векторной величиной. После подстановки выражений для векторов электромагнитного поля вида (2) в систему уравнений (1) получаем «алгебраическую» систему уравнений:
- радиус-вектор точки наблюдения. Ниже круговую частоту принимаем постоянной действительной величиной, а волновой вектор – постоянной, возможно комплексной векторной величиной. После подстановки выражений для векторов электромагнитного поля вида (2) в систему уравнений (1) получаем «алгебраическую» систему уравнений:
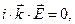
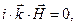
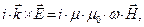
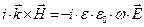 . (3)
. (3)
Круговая частота волны и волновой вектор связаны между собой дисперсионным уравнением
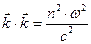 . (4)
. (4)
Здесь 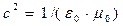 - квадрат скорости распространения электромагнитной волны в вакууме,
- квадрат скорости распространения электромагнитной волны в вакууме, 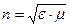 - «абсолютный» показатель преломления среды, определённый по условию как действительная положительная величина. Действительные значения волнового вектора характерны для однородных электромагнитных волн. Дисперсионное уравнение (4) допускает существование комплексной формы волнового вектора
- «абсолютный» показатель преломления среды, определённый по условию как действительная положительная величина. Действительные значения волнового вектора характерны для однородных электромагнитных волн. Дисперсионное уравнение (4) допускает существование комплексной формы волнового вектора
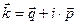 , (5)
, (5)
для электромагнитной волны в непроводящей среде, при этом уравнение (4) приобретает форму системы двух уравнений
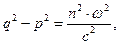
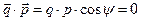 , (6)
, (6)
где векторы 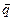 и
и 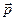 являются действительными величинами, ортогональными друг другу (
являются действительными величинами, ортогональными друг другу ( 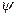 - угол между рассматриваемыми векторами).
- угол между рассматриваемыми векторами).
Заметим, что распространённое представление волнового вектора в комплексной форме [2] с условием совпадения пространственной ориентации действительной и мнимой составляющих является частным случаем, в рассматриваемой ситуации (непроводящие среды) такое представление влечёт необходимость обращения в нуль одного из слагаемых. Для падающей и отражённой волн в нуль обращаются мнимые составляющие, а для преломлённой волны – действительная составляющая волнового вектора. Ниже это будет показано как результат рассмотрения условий сопряжения решений для волнового электромагнитного поля в первой среде (падающая и отражённая волны) и во второй среде (преломлённая волна).
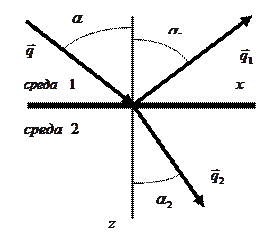
Предположим, что электромагнитная волна падает на плоскую границу раздела двух диэлектриков из первой среды и частично проникает во вторую среду, в декартовой системе координат граница раздела описывается уравнением 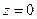 , ось
, ось 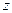 направлена во вторую среду, ось
направлена во вторую среду, ось 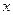 направлена так, чтобы проекция волнового вектора падающей волны на это направление была положительной, ось
направлена так, чтобы проекция волнового вектора падающей волны на это направление была положительной, ось 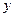 достраиваем таким образом, чтобы система координат оказалась «правой». Физические величины отражённой волны отметим с помощью нижнего индекса 1, физические величины преломлённой волны отметим с помощью нижнего индекса 2, физические величины падающей волны оставим без нижнего индекса.
достраиваем таким образом, чтобы система координат оказалась «правой». Физические величины отражённой волны отметим с помощью нижнего индекса 1, физические величины преломлённой волны отметим с помощью нижнего индекса 2, физические величины падающей волны оставим без нижнего индекса.
Пространственная ориентация волновых векторов 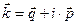 ,
, 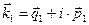 и
и 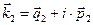 в общем случае должна быть определена отдельно для действительных и мнимых составляющих, реализовать это условие можно, задавая углы падения, отражения и преломления для действительных компонент волновых векторов
в общем случае должна быть определена отдельно для действительных и мнимых составляющих, реализовать это условие можно, задавая углы падения, отражения и преломления для действительных компонент волновых векторов 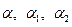 и мнимых компонент волновых векторов
и мнимых компонент волновых векторов 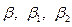 соответственно в «действительной» плоскости падения, определяемой ориентацией вектора
соответственно в «действительной» плоскости падения, определяемой ориентацией вектора 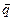 , и в «мнимой» плоскости падения, определяемой вектором
, и в «мнимой» плоскости падения, определяемой вектором 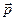 .
.

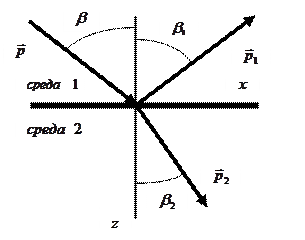
Электромагнитное поле должно удовлетворять известным условиям сопряжения на поверхности раздела двух сред. Эти условия должны быть выполнены для произвольного момента времени и для произвольной точки поверхности раздела. Если векторы электромагнитного поля имеют структуру (2), то следствием условий сопряжения является требование совпадения мгновенной фазы колебаний при условии 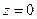 :
:
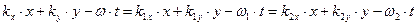 ,
, 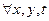 . (7)
. (7)
Из этих условий следует
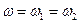 ,
, 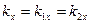 ,
, 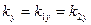 . (8)
. (8)
Принимаем (по условию), что падающая волна является однородной
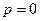 . (9)
. (9)
Цепочку соотношений 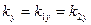 можно удовлетворить, если выбрать подходящим способом систему декартовых координат (
можно удовлетворить, если выбрать подходящим способом систему декартовых координат ( 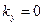 ).
).
Легко видеть, что должны быть выполнены следующие условия:
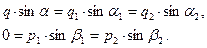 (10)
(10)
Если предположить, что 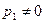 , то справедливы дисперсионные уравнения
, то справедливы дисперсионные уравнения
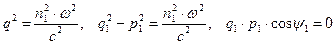 . (11)
. (11)
Поскольку 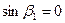 , вектор
, вектор 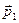 параллелен оси
параллелен оси 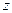 , но при этом векторы
, но при этом векторы 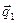 и
и 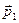 взаимно ортогональны, значит, вектор
взаимно ортогональны, значит, вектор 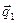 параллелен оси
параллелен оси 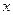 , т.е.
, т.е. 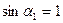 . В этом случае справедливо соотношение
. В этом случае справедливо соотношение
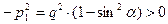 . (12)
. (12)
Поскольку величина 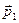 определена как действительная векторная величина, полученный результат позволяет заключить, что отражённая волна не может быть неоднородной:
определена как действительная векторная величина, полученный результат позволяет заключить, что отражённая волна не может быть неоднородной:
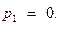 (13)
(13)
Если отражённая волна является однородной, то справедливы соотношения
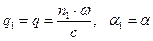 (14)
(14)
- модули волновых векторов падающей и отражённой волны одинаковы, а угол падения равен углу отражения.
Преломлённая волна предполагается неоднородной
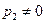 , (15)
, (15)
вектор 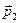 направлен параллельно оси
направлен параллельно оси 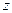 , вектор
, вектор 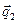 ему ортогонален, т.е. направлен параллельно оси
ему ортогонален, т.е. направлен параллельно оси 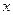 , значит,
, значит, 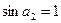 . В этих условиях легко получить соотношения:
. В этих условиях легко получить соотношения:
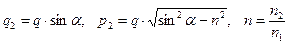 . (16)
. (16)
Модуль вектора 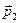 должен быть действительной положительной величиной, т.е. явление полного внутреннего отражения может иметь место только при выполнении условия
должен быть действительной положительной величиной, т.е. явление полного внутреннего отражения может иметь место только при выполнении условия
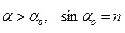 , (17)
, (17)
где 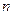 - относительный показатель преломления,
- относительный показатель преломления, 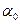 - предельный угол.
- предельный угол.
Дальнейшее исследование связано с установлением зависимостей между комплексными амплитудами векторных электромагнитных волн, его удобно проводить отдельно для s-поляризованной и р-поляризованной падающих волн.
S-поляризация падающей волны.
В рассматриваемом случае вектор амплитуды напряжённости электрического поля перпендикулярен плоскости падения электромагнитной волны, образованной волновым вектором падающей волны и нормалью к поверхности раздела сред:
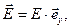 (18)
(18)
а волновой вектор падающей волны имеет вид:
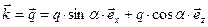 . (19)
. (19)
Используя соответствующее соотношение системы уравнений (3), получим выражение для вектора амплитуды напряжённости магнитного поля падающей волны:
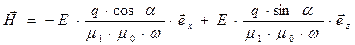 . (20)
. (20)
Амплитуды 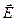 и
и 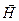 падающей волны являются вещественными (действительными) величинами.
падающей волны являются вещественными (действительными) величинами.
Волновой вектор отражённой волны запишем с учётом полученных выше результатов:
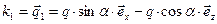 . (21)
. (21)
Естественно предположить, что вектор амплитуды напряжённости электрического поля отражённой волны 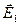 также направлен вдоль оси
также направлен вдоль оси 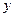 (ниже убедимся, что это предположение справедливо):
(ниже убедимся, что это предположение справедливо):
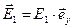 , (22)
, (22)
величина 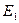 подлежит определению.
подлежит определению.
Из системы уравнений Максвелла, записанных для плоских гармонических волн в амплитудной форме следует зависимость:
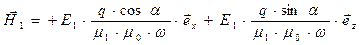 . (23)
. (23)
Для преломлённой волны в рамках сделанных выше предположений справедливы зависимости:
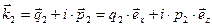 , (24)
, (24)
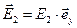 , (25)
, (25)
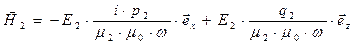 . (26)
. (26)
В этих зависимостях величины 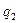 и
и 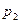 определены выше, а величина
определены выше, а величина 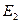 подлежит определению.
подлежит определению.
Вычислим «геометрическую» длину амплитуд напряжённости магнитного поля, определённых выше проекциями на оси декартовой системы координат:
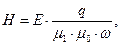
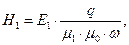
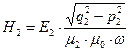 . (27)
. (27)
Рассмотрим условия непрерывности касательных компонент векторов напряжённости электрического и магнитного полей на границе раздела двух диэлектриков. Условие непрерывности касательных компонент векторов напряжённости электрического поля вдоль оси 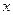 выполняется тривиально. Условие непрерывности касательных компонент векторов напряжённости электрического поля вдоль оси
выполняется тривиально. Условие непрерывности касательных компонент векторов напряжённости электрического поля вдоль оси 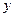 приводит к уравнению:
приводит к уравнению:
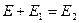 . (28)
. (28)
Условие непрерывности касательных компонент векторов напряжённости магнитного поля вдоль оси 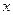 (в предположении, что поверхностных токов проводимости на границе раздела нет) имеет вид:
(в предположении, что поверхностных токов проводимости на границе раздела нет) имеет вид:
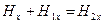 . (29)
. (29)
Условие непрерывности касательных компонент векторов напряжённости магнитного поля вдоль оси 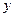 выполняется тривиально.
выполняется тривиально.
Решение однородной системы двух алгебраических уравнений приводит к параметрическим зависимостям (коэффициенты Френеля):
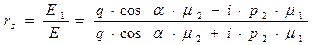 , (30)
, (30)
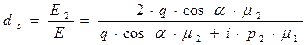 . (31)
. (31)
Величины 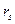 и
и 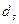 являются комплексными величинами, это соответствует существованию сдвига по мгновенной фазе колебаний в отражённой и преломлённой волнах по сравнению с мгновенной фазой колебаний в падающей волне. Для отражённой волны сдвиг фаз определяется соотношением
являются комплексными величинами, это соответствует существованию сдвига по мгновенной фазе колебаний в отражённой и преломлённой волнах по сравнению с мгновенной фазой колебаний в падающей волне. Для отражённой волны сдвиг фаз определяется соотношением
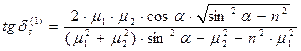 . (32)
. (32)
Явление сдвига фаз для отражённой волны можно описать более компактным способом. В теории функций комплексного переменного известно легко проверяемое соотношение
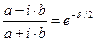 ,
, 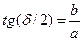 . (33)
. (33)
Воспользуемся этим результатом:
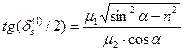 . (34)
. (34)
Легко видеть, что модуль коэффициента 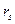 равен единице:
равен единице:
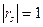 , (35)
, (35)
что служит основанием для утверждения, что отражение является «полным».
Для преломлённой волны имеет место соотношение
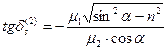 . (36)
. (36)
Заметим при этом, что комплексная величина 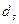 отлична от нуля.
отлична от нуля.
Интересно отметить, что имеется возможность вычислить «магнитные» коэффициенты Френеля:
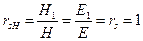 , (37)
, (37)
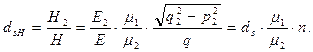 (38)
(38)
Обратим внимание читателя на то, что отношения амплитуд напряжённостей магнитного поля и напряжённостей электрического поля во второй среде друг с другом не совпадают. Здесь, как и ранее, легко выявляется смысл понятия «полное внутреннее отражение» ( 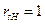 ) и остаётся вопрос о физическом смысле отличия от нуля величины
) и остаётся вопрос о физическом смысле отличия от нуля величины 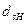 .
.
Выражения для напряжённости магнитного поля падающей, отражённой и преломлённой волны (эти зависимости получены выше) становятся полностью определёнными.
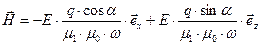 , (39)
, (39) 
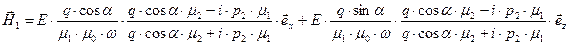 , (40)
, (40)
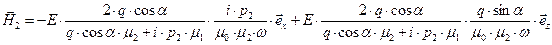 . (41)
. (41)
Проверим условия непрерывности нормальных компонент вектора магнитной индукции:
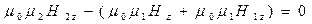 . (42)
. (42)
Если в приведённое условие подставить полученные выше величины, убеждаемся, что оно превращается в тождество, нормальные компоненты индукции магнитного поля непрерывны при переходе через границу раздела сред.
Поскольку векторы напряжённости электрического поля параллельны поверхности раздела сред, то поверхностная плотность сторонних и индуцированных электрических зарядов на поверхности раздела сред равна нулю.
Перейдём к изучению плотностей потоков электромагнитной энергии в окрестности граница раздела двух диэлектрических сред.
Введём обозначение мгновенной фазы колебаний рассматриваемых электромагнитных волн (пока не учитываем значение сдвига фазы колебаний, скрытого в комплексной форме записи амплитуды электромагнитной волны)
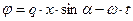 (43)
(43)
и с помощью известной формулы Эйлера запишем "развёрнутые" выражения для векторных электромагнитных волн в окрестности (т.е. на) поверхности раздела сред:
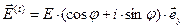 ,
, 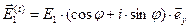 ,
, 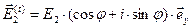 (44)
(44)
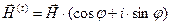 ,
, 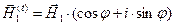 ,
, 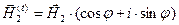 . (45)
. (45)
Учитывая то обстоятельство, что комплексные амплитуды действительно являются комплексными величинами, вычислим выражения для действительных амплитуд напряжённостей электрического и магнитного полей в первой и второй средах, справедливые для произвольных моментов времени 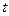 и координаты
и координаты 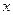 :
:
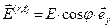 ,
, 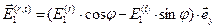 ,
, 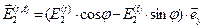 , (46)
, (46)
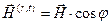 ,
, 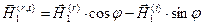 ,
, 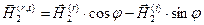 . (47)
. (47)
Здесь использованы обозначения:
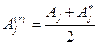 ,
, 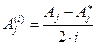 , (48)
, (48)
верхний индекс 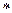 использован для обозначения комплексно сопряжённой величины. Приведём соответствующие выражения для амплитуд напряжённости электрического и магнитного поля в отражённой волне
использован для обозначения комплексно сопряжённой величины. Приведём соответствующие выражения для амплитуд напряжённости электрического и магнитного поля в отражённой волне
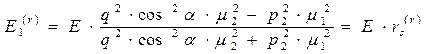 , (49)
, (49)
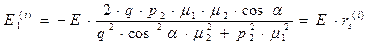 , (50)
, (50)
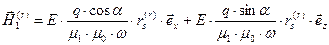 , (51)
, (51)
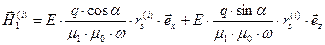 (52)
(52)
и в преломлённой волне
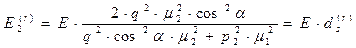 , (53)
, (53)
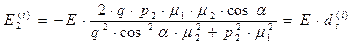 , (54)
, (54)
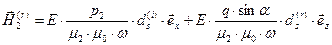 , (55)
, (55)
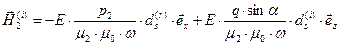 . (56)
. (56)
Используя полученные результаты, можно вычислить выражения для векторов Умова-Пойнтинга в падающей, отражённой и преломлённой волнах, справедливые для произвольного момента времени t и произвольной точки поверхности x:
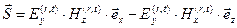 , (57)
, (57)
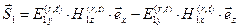 , (58)
, (58)
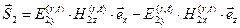 . (59)
. (59)
В первую очередь нас интересует баланс нормальных компонент векторов Умова-Пойнтинга в произвольной точке поверхности раздела в произвольный момент времени.
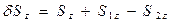 . (60)
. (60)
Подставляя в рассматриваемое выражение входящие в него «первичные» зависимости, определённые выше, можно убедиться в справедливости утверждения:
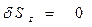 . (61)
. (61)
Отсюда следует, что в произвольной точке поверхности раздела диэлектрических сред в любой момент времени выполняется условие баланса плотностей потока электромагнитной энергии. Энергия электромагнитного поля не накапливается на поверхности раздела в течение произвольного промежутка времени внутри периода колебаний.
Осреднённые величины нормальных компонент векторов Умова-Пойнтинга падающей волны, отражённой волны и преломлённой волны на поверхности раздела сред определяются выражениями типа:
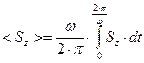 . (62)
. (62)
Если уравнение баланса нормальных компонент плотности потоков энергии выполняется для каждого момента времени, оно будет выполнено и для осреднённых величин:
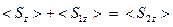 . (63)
. (63)
Полученный результат позволяет ввести в рассмотрение коэффициент отражения и коэффициент пропускания
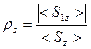 ,
, 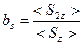 . (64)
. (64)
Непосредственным вычислением можно убедиться в справедливости
результатов:
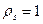 ,
, 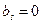 . (65)
. (65)
Приходим к выводу, что термин «полное внутреннее отражение» является следствием рассмотрения осреднённых нормальных составляющих векторов Умова-Пойнтинга.
Вернёмся к анализу зависимостей от времени мгновенных значений нормальных компонент векторов Умова-Пойнтинга. После подстановки полученных выше результатов в интересующие нас выражения можно получить следующие зависимости:
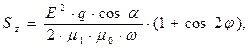 (66)
(66)
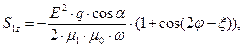 (67)
(67)
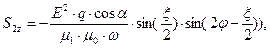 (68)
(68)
где 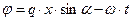 , (69)
, (69) 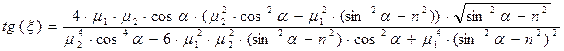 . (70)
. (70)
Значительно удобнее пользоваться эквивалентным соотношением
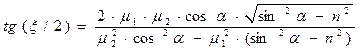 . (71)
. (71)
Характер зависимостей от мгновенной фазы колебаний касательных компонент векторов Умова-Пойнтинга падающей, отражённой и преломлённой волн продемонстрируем с помощью соотношений
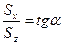 ,
, 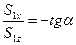 , (72)
, (72)
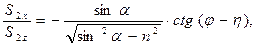
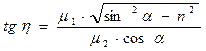 . (73)
. (73)
Фазы колебаний касательных компонент векторов Умова-Пойнтинга падающей и отражённой волн совпадают с фазами колебаний соответствующих нормальных компонент векторов Умова-Пойнтинга. Изменение с течением времени касательной компоненты вектора Умова-Пойнтинга преломлённой волны описывается более сложной зависимостью: приведённое выше отношение 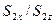 , оказывается, зависит от мгновенной фазы электромагнитной волны.
, оказывается, зависит от мгновенной фазы электромагнитной волны.
Дата добавления: 2017-09-01; просмотров: 2697;











