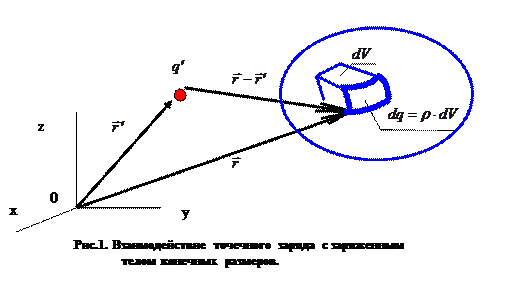
Взаимодействие точечного заряда с заряженным телом.

Рассмотрим взаимодействие сосредоточенного электрического заряда 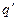, расположенного в точке пространства, радиус-вектор которой 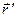, с телом 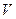с объёмной плотностью электрического заряда 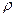. Пространственное положение произвольной точки рассматриваемого тела описывается радиус-вектором 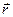. Выделим в объёме 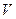элемент объёма 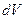(рис.1) и запишем выражение для электрического заряда выделенного элемента объёма: 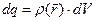. Этот заряд по определению можно считать точечным, поэтому силу, действующую на заряд 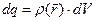со стороны точечного заряда 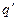, вычислим в соответствии с законом Кулона:

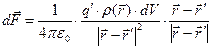. (1)

Воспользуемся принципом суперпозиции. Результирующую силу воздействия сосредоточенного заряда на совокупность электрических зарядов, распределённых по объёму 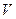можно вычислить с помощью квадратуры:

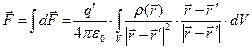.(2)

Выпишем выражения для проекций результирующей силы 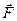на оси декартовой системы координат:

,

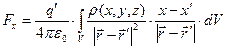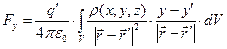,(3)

,

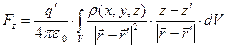где (x,y,z) ,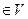

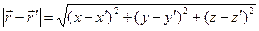. (4)

По аналогии с предыдущим разделом можно вычислить модуль вектора 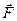и его направляющие косинусы.

Следует обратить внимание на структурную идентичность выкладок, выполненных в настоящем и двух предыдущих разделах. Можно говорить о едином методическом приёме рассмотрения подобных физических ситуаций. Ниже рассмотрим несколько более сложные случаи взаимодействия электрически заряженных тел.