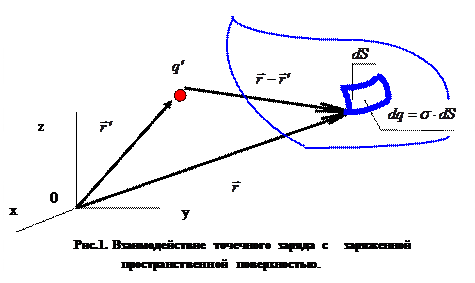
Взаимодействие точечного заряда с заряженным участком поверхности.

Вычислим силу, с которой точечный электрический заряд 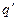, расположенный в точке пространства, радиус-вектор которой 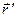, действует на участок пространственной поверхности 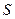, если на рассматриваемой поверхности известна поверхностная плотность электрического заряда 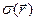(рис.1). Для этого выделим на рассматриваемой поверхности элемент поверхности 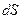, положение которого в пространстве радиус-вектором 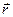, и вычислим величину электрического заряда, сосредоточенного на этом элементе 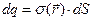. Воздействие сосредоточенного заряда 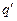на рассматриваемый элементарный заряд 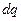подчиняется закону Кулона:

.(1)

Воспользуемся принципом суперпозиции. Результирующую силу воздействия сосредоточенного заряда на совокупность электрических зарядов, распределённых по пространственной поверхности 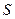можно вычислить с помощью квадратуры:

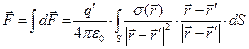.(2)

Если проекции радиус-вектора 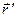суть { 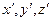}, а проекции радиус-вектора 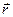- {x,y,z}, проекции результирующей силы 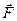на оси декартовой системы координат принимают вид:

,

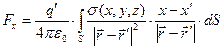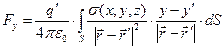,(3)

,

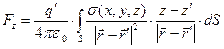где (x,y,z) ,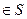

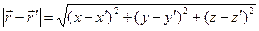. (4)

Квадратуры (3) в общем случае вычисляются с помощью численных методов и современного математического обеспечения персональных компьютеров. Получив численные значения проекци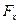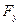й , и 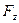результирующей силы 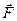, можно рассчитать модуль вектора 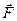и соответствующие направляющие косинусы.

Таким образом, взаимодействие точечного заряда с заряженным участком пространственной поверхности полностью описано.