Поле сосредоточенного электрического заряда, движущегося в вакууме по прямой с постоянной скоростью.
Электрическое и магнитное поле равномерно и прямолинейно движущегося в вакууме сосредоточенного электрического заряда имеют самый простой вид в системе отсчёта 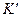 , в которой этот заряд покоится, создавая вокруг себя известное электростатическое поле. Магнитное поле в этой системе отсчёта тождественно равно нулю: неподвижные электрические заряды не создают магнитное поле. Вместе с тем, рассматривая этот же заряд в произвольной инерциальной системе отсчёта
, в которой этот заряд покоится, создавая вокруг себя известное электростатическое поле. Магнитное поле в этой системе отсчёта тождественно равно нулю: неподвижные электрические заряды не создают магнитное поле. Вместе с тем, рассматривая этот же заряд в произвольной инерциальной системе отсчёта 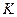 , замечаем, что он движется со скоростью
, замечаем, что он движется со скоростью 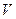 , т.е. со скоростью системы отсчёта
, т.е. со скоростью системы отсчёта 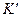 относительно системы отсчёта
относительно системы отсчёта 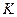 . Заметим, что всегда имеется возможность ориентировать систему координат
. Заметим, что всегда имеется возможность ориентировать систему координат 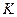 таким образом, чтобы направление движения электрического заряда совпадало с положительным направлением оси
таким образом, чтобы направление движения электрического заряда совпадало с положительным направлением оси 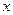 .
.
Прямолинейно движущийся электрический заряд подобен прямолинейному току. Силовые линии магнитного поля, образованного прямолинейным током, являются окружностями. Центры этих окружностей расположены на прямой линии, вдоль которой движется электрический заряд, а плоскости окружностей перпендикулярны траектории заряда. Формулы специальной теории относительности позволяют провести преобразования составляющих электромагнитного поля и выяснить характер зависимостей электромагнитного поля равномерно движущегося сосредоточенного электрического поля в релятивистском приближении и в случае относительно медленного движения заряда.
Рассмотрим в начале координат системы 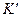 точечный электрический заряд
точечный электрический заряд 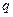 . Электрическое поле в этой системе координат (трёхмерное представление!) имеет вид
. Электрическое поле в этой системе координат (трёхмерное представление!) имеет вид
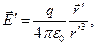 (1) где
(1) где 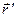 - радиус-вектор точки наблюдения в системе координат
- радиус-вектор точки наблюдения в системе координат 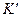 . Магнитное поле в системе координат
. Магнитное поле в системе координат 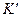 равно нулю:
равно нулю:
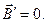 (2) В проекциях на оси декартовой системы координат символическая форма записи (1) и (2) превращается в следующие соотношения:
(2) В проекциях на оси декартовой системы координат символическая форма записи (1) и (2) превращается в следующие соотношения:
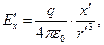
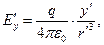
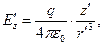 (3)
(3)
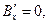
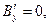
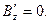 (4) Воспользуемся трёхмерными формулами преобразования векторных величин электромагнитного поля (3)-(4) при преобразовании координат по Лоренцу (зависимости (1) раздела 13.2.1) и запишем
(4) Воспользуемся трёхмерными формулами преобразования векторных величин электромагнитного поля (3)-(4) при преобразовании координат по Лоренцу (зависимости (1) раздела 13.2.1) и запишем
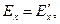
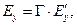
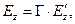 (5)
(5)
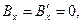
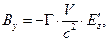
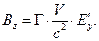 (6)
(6)
Здесь, как обычно, 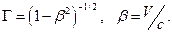 В выражениях (5) и (6) остаётся только выразить штрихованные координаты через координаты системы
В выражениях (5) и (6) остаётся только выразить штрихованные координаты через координаты системы 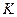 :
:
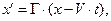
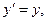
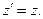 (7)
(7)
В этом случае
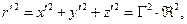
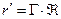 ,
, 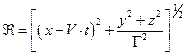 . (8)
. (8)
С учётом соотношений (7) и (8) запишем выражения для составляющих вектора электрического поля в системе отсчёта 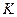 :
:
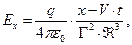
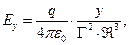
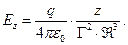 (9)
(9)
Для составляющих магнитного поля аналогично получаем:
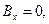
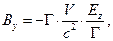
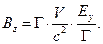 (10)
(10)
Соотношения (10) в символической форме записи предельно компактны и информативны
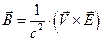 . (11)
. (11)
Соотношения (9) значительно упрощаются для момента времени 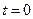 , когда электрический заряд находится в начале системы координат
, когда электрический заряд находится в начале системы координат 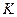 :
:
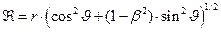 , (12)
, (12)
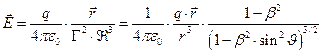 . (13)
. (13)
В соотношениях (12) и (13) 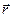 - радиус-вектор точки наблюдения,
- радиус-вектор точки наблюдения, 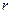 - модуль этого вектора,
- модуль этого вектора, 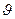 - угол между радиус-вектором точки наблюдения и направлением скорости движения электрического заряда
- угол между радиус-вектором точки наблюдения и направлением скорости движения электрического заряда 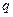 , т.е. осью х. Если электрический заряд неподвижен (
, т.е. осью х. Если электрический заряд неподвижен ( 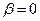 ), напряжённость электрического поля является сферически симметричной: вектор
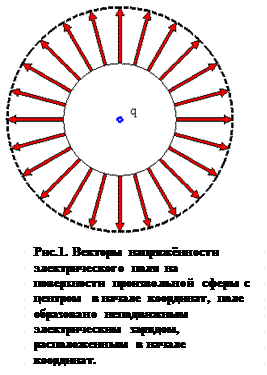
), напряжённость электрического поля является сферически симметричной: вектор 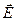 при этом является радиальным, а его модуль одинаков во всех точках сферы с центром в начале координат (Рис.1).
при этом является радиальным, а его модуль одинаков во всех точках сферы с центром в начале координат (Рис.1).
|
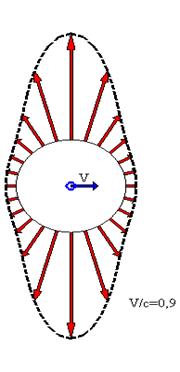
Интересно, что в случае, когда электрический заряд движется ( 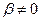 ), даже если он находится в рассматриваемый момент времени в начале координат системы К, происходит трансформация распределения напряжённости электрического поля: оно остаётся радиальным, но модуль вектора напряжённости в различных точках поверхности контрольной сферы с центром в начале координат зависит от угла
), даже если он находится в рассматриваемый момент времени в начале координат системы К, происходит трансформация распределения напряжённости электрического поля: оно остаётся радиальным, но модуль вектора напряжённости в различных точках поверхности контрольной сферы с центром в начале координат зависит от угла 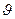 (Рис2). Степень трансформации увеличивается с ростом величины параметра
(Рис2). Степень трансформации увеличивается с ростом величины параметра 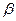 .
.
Минимальное значение напряжённости электрического поля реализуется в точках описанной выше контрольной сферы для углов 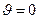 и
и 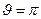 :
:
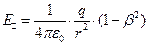 . (14)
. (14)
Максимальное значение напряжённости электрического поля реализуется в точках контрольной сферы для углов 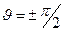 :
:
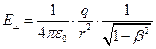 . (15)
. (15)
Заметим, что движение заряженной частицы со скоростью света ( 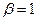 ) порождало бы бесконечно большую силу воздействия на пробный электрический заряд, координата х которого равнялась бы нулю.
) порождало бы бесконечно большую силу воздействия на пробный электрический заряд, координата х которого равнялась бы нулю.
Допустим, что наблюдатель находится на удалении от начала координат на расстояние 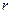 , а радиус-вектор точки наблюдения составляет с положительным направлением оси х угол
, а радиус-вектор точки наблюдения составляет с положительным направлением оси х угол 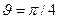 . Пусть электрический заряд движется со скоростью
. Пусть электрический заряд движется со скоростью 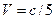 и при
и при 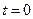 проходит начало координат. Введём в рассмотрение безразмерный параметр
проходит начало координат. Введём в рассмотрение безразмерный параметр 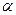 , пропорциональный времени t :
, пропорциональный времени t : 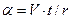 . В этом случае справедливы зависимости:
. В этом случае справедливы зависимости:
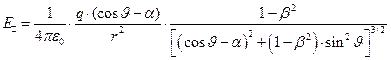 , (16)
, (16)
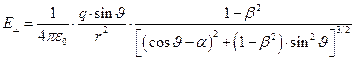 . (17)
. (17)
Определим характерное значение напряжённости электрического поля
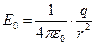 . (18)
. (18)
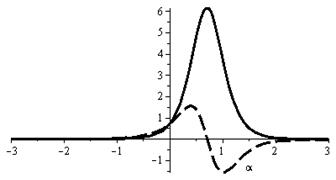
Построим графики функций 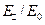 и
и 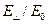 в зависимости от параметра
в зависимости от параметра 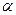 , пропорционального времени наблюдения
, пропорционального времени наблюдения 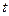 , при значениях
, при значениях 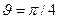 и
и 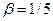 (рис.3).
(рис.3).
|
В соответствии с рис. 3 наблюдатель фиксирует сначала положительное переменное во времени значение продольной напряжённости электрического поля, потом отрицательное значение этой величины (сила, действующая на элементарный положительный пробный электрический заряд изменяет своё направление). Поперечное значение напряжённости электрического поля сначала возрастает до максимальной положительной величины, потом монотонно убывает до нуля. Таким образом, в точке наблюдения имеет место переменное во времени электрическое поле.
Полученные выше аналитические выражения для силовых характеристик электромагнитного поля, образованного сосредоточенным электрическим зарядом, движущимся в вакууме по прямой с постоянной скоростью, позволяют проверить их соответствие основным интегральным законам классической электродинамики.
Интегральная форма теоремы Гаусса для вектора 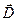 . Вычислим величину потока векторного поля (13) через поверхность сферы произвольного радиуса с центром в начале координат (электрический заряд
. Вычислим величину потока векторного поля (13) через поверхность сферы произвольного радиуса с центром в начале координат (электрический заряд 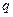 в момент времени
в момент времени 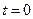 находится в начале координат):
находится в начале координат):
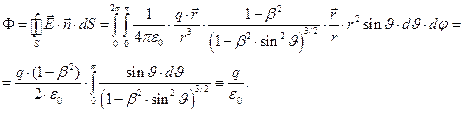 (19)
(19)
Легко видеть, что, несмотря на трансформацию распределения напряжённости электрического поля, вызванную движением электрического заряда, теорема Гаусса для вектора напряжённости электрического поля для рассматриваемого частного случая выполняется (случай произвольной замкнутой поверхности мы не рассматриваем).
Рассмотрим произвольный момент времени, пусть при этом электрический заряд находится в произвольной точке оси х, скорость его движения остаётся равной величине V . Для удобства введём безразмерный параметр 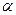 :
:
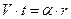 , (20)
, (20)
где, как и раньше, 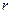 - модуль радиус-вектора точки наблюдения. Величина
- модуль радиус-вектора точки наблюдения. Величина 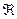 по выражению (8) приобретает вид:
по выражению (8) приобретает вид:
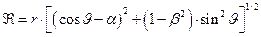 . (21)
. (21)
Выпишем явное выражение для вектора напряжённости электрического поля в произвольной точке наблюдения в системе К:
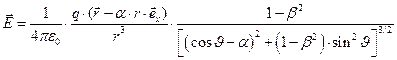 , (22)
, (22)
где 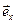 - орт направления вдоль оси координат х. Рассмотрим в качестве контрольной поверхности поверхность сферы радиуса
- орт направления вдоль оси координат х. Рассмотрим в качестве контрольной поверхности поверхность сферы радиуса 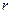 с центром в начале координат. Напомним, что электрический заряд в рассматриваемый момент времени находится в произвольной точке оси х. Вычислим поток вектора (22) через рассматриваемую контрольную поверхность:
с центром в начале координат. Напомним, что электрический заряд в рассматриваемый момент времени находится в произвольной точке оси х. Вычислим поток вектора (22) через рассматриваемую контрольную поверхность:
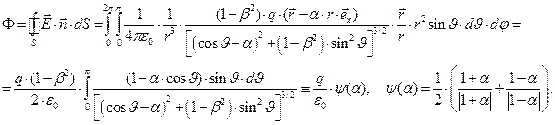 (23)
(23)
Заметим, что полученный результат справедлив при произвольном значении параметра 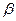 .
.
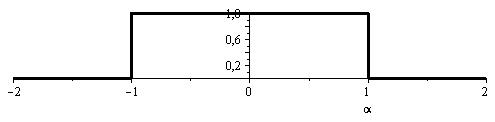
График зависимости 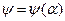 представлен на рис.4:
представлен на рис.4:
|
Физический смысл полученного результата. Если выполнено условие 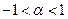 , то электрический заряд
, то электрический заряд 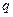 находится внутри контрольной поверхности, при этом
находится внутри контрольной поверхности, при этом 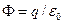 .
.
Если выполнено условие 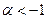 или условие
или условие 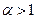 , то электрический заряд
, то электрический заряд 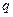 находится вне контрольной поверхности, при этом
находится вне контрольной поверхности, при этом 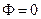 . Видим, что и в этом случае выполняется интегральная теорема Гаусса для вектора напряжённости электрического поля.
. Видим, что и в этом случае выполняется интегральная теорема Гаусса для вектора напряжённости электрического поля.
Закон полного тока в интегральной форме. В плоскости Oyz (x=0) рассмотрим окружность радиуса а с центром в начале координат (рис. 5).
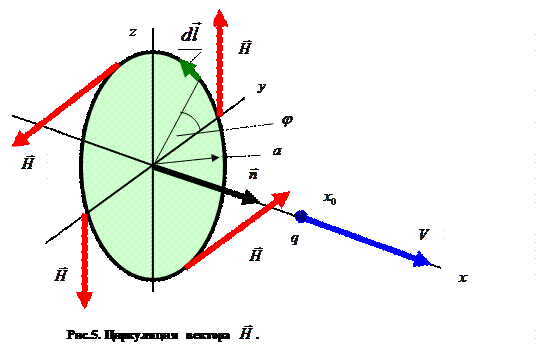
Координаты точки наблюдения на этой окружности суть 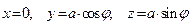 . Пусть в рассматриваемый момент времени положение сосредоточенного электрического заряда
. Пусть в рассматриваемый момент времени положение сосредоточенного электрического заряда 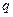 описывается координатой
описывается координатой 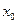 . Параметр
. Параметр 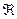 , входящий в выражения (9) для компонент вектора напряжённости электрического поля, принимает вид:
, входящий в выражения (9) для компонент вектора напряжённости электрического поля, принимает вид:
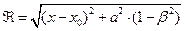 ,
, 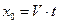 . (24)
. (24)
При записи выражения (24) сохранено обозначение координаты х чтобы не потерять геометрический смысл выполняемых ниже операций. Соотношениями (9) и (10) определены компоненты вектора напряжённости электрического поля и компоненты вектора магнитной индукции магнитного поля для точек рассматриваемой окружности. Легко видеть, что модуль вектора магнитной индукции 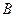 для точек окружности равен
для точек окружности равен
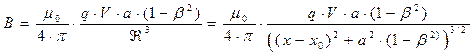 . (25)
. (25)
Выражение для модуля вектора напряжённости магнитного поля Н совпадает с выражением (25), если последнее разделить на магнитную постоянную. Анализируя выражения (10) с учётом координат точек рассматриваемой окружности, замечаем, что вектор 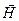 по направлению совпадает с направлением касательной к окружности в каждой рассматриваемой точке и сохраняет свою величину. В этом случае циркуляция вектора
по направлению совпадает с направлением касательной к окружности в каждой рассматриваемой точке и сохраняет свою величину. В этом случае циркуляция вектора 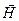 по рассматриваемой окружности в направлении увеличения угловой координаты
по рассматриваемой окружности в направлении увеличения угловой координаты 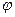 составит величину
составит величину
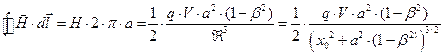 . (26)
. (26)
Заметим, что направление обхода контрольной круговой области, ограниченной окружностью радиуса а, согласовано с направлением нормали к этой поверхности, если нормаль совпадет с положительным направлением оси х.
Вычислим поток вектора 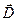 рассматриваемого электрического поля через плоскую поверхность, ограниченную контрольной окружностью радиуса а с центром в начале координат
рассматриваемого электрического поля через плоскую поверхность, ограниченную контрольной окружностью радиуса а с центром в начале координат 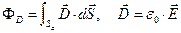 . Для этого необходимо компоненту электрического поля
. Для этого необходимо компоненту электрического поля 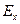 по выражению (9) умножить на величину электрической постоянной и рассмотреть эту величину в точке наблюдения
по выражению (9) умножить на величину электрической постоянной и рассмотреть эту величину в точке наблюдения 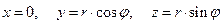 . Переопределим параметр
. Переопределим параметр 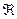
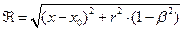 (27)
(27)
и получим:
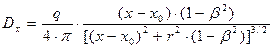 . (28)
. (28)
Проинтегрируем выражение (28) по площади круга радиуса а с учётом осевой симметрии:
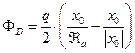 ,
, 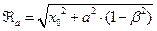 ,
, 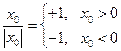 . (29)
. (29)
Продифференцируем выражение (29) по времени, учитывая, что зависимость 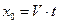 :
:
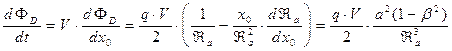 . (30)
. (30)
Сравнивая между собой выражения (26) и (30), убеждаемся, что независимо от рассматриваемого момента времени (т.е. для произвольного значения величины 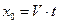 ), правые части этих выражений тождественно равны друг другу. Пусть не в самой общей форме, но для рассматриваемой физической ситуации, очевидно, что закон полного тока в интегральной формулировке для релятивистских скоростей движения электрического заряда выполняется.
), правые части этих выражений тождественно равны друг другу. Пусть не в самой общей форме, но для рассматриваемой физической ситуации, очевидно, что закон полного тока в интегральной формулировке для релятивистских скоростей движения электрического заряда выполняется.
Закон сохранения энергии электромагнитного поля.Проверим выполнение теоремы Пойнтинга (в интегральной форме) для электромагнитного поля, описанного соотношениями (9) и (10): сосредоточенный электрический заряд движется вдоль оси х с постоянной скоростью V и в произвольный рассматриваемый момент времени находится в точке 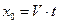 . Для произвольной точки наблюдения внутри сферы радиуса а с центром в начале координат системы отсчёта К запишем выражение для объёмной плотности энергии электрического поля
. Для произвольной точки наблюдения внутри сферы радиуса а с центром в начале координат системы отсчёта К запишем выражение для объёмной плотности энергии электрического поля
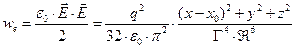 (31)
(31)
и выражение для объёмной плотности энергии магнитного поля:
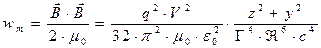 . (32)
. (32)
Объединяя результаты вычислений (31) и (32) с учётом определения скорости света в вакууме, получаем выражение для объёмной плотности энергии электромагнитного поля:
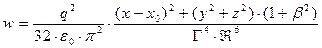 . (33)
. (33)
|
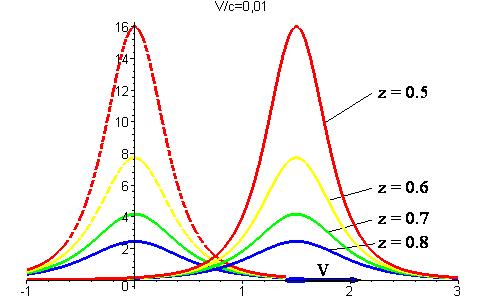
На рисунке 6 показаны зависимости относительной величины 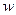 объёмной плотности энергии электромагнитного поля от продольной пространственной координаты (с учётом осевой симметрии, очевидно) для момента времени, когда электрический заряд находился в начале координат, и для момента времени, когда его относительная координата равнялась 1,5. В качестве переменного параметра принято расстояние (относительная величина) от точки наблюдения до оси х, т.е. поперечная координата точки наблюдения. Зависимости построены для значения параметра
объёмной плотности энергии электромагнитного поля от продольной пространственной координаты (с учётом осевой симметрии, очевидно) для момента времени, когда электрический заряд находился в начале координат, и для момента времени, когда его относительная координата равнялась 1,5. В качестве переменного параметра принято расстояние (относительная величина) от точки наблюдения до оси х, т.е. поперечная координата точки наблюдения. Зависимости построены для значения параметра 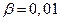 , что соответствует скорости заряда V~3 000 км/c. Результаты расчётов объёмной плотности энергии электромагнитного поля (рис. 6) согласуются с результатами «уплощения» поля напряжённости электрического поля (рис.2). Важно отметить, что электрический заряд при движении вдоль прямой линии с постоянной скоростью «несёт с собой» электромагнитное поле: штрихованные линии переходят в соответствующие сплошные линии (рис.6).
, что соответствует скорости заряда V~3 000 км/c. Результаты расчётов объёмной плотности энергии электромагнитного поля (рис. 6) согласуются с результатами «уплощения» поля напряжённости электрического поля (рис.2). Важно отметить, что электрический заряд при движении вдоль прямой линии с постоянной скоростью «несёт с собой» электромагнитное поле: штрихованные линии переходят в соответствующие сплошные линии (рис.6).
Продифференцируем полученное выше выражение (33) по времени:
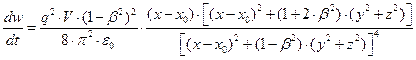 . (34)
. (34)
Проинтегрируем выражение (34) по объёму сферы радиуса a с центром в начале координат и получим скорость изменения энергии электромагнитного поля в объёме сферы с течением времени. Непосредственное интегрирование удобно провести в сферической системе координат с учётом осевой симметрии поля относительно продольной оси х. К сожалению, в рассматриваемом случае удалось записать ответ только в форме двойной квадратуры
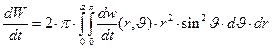 . (35)
. (35)
Теперь, пользуясь выражениями (9) и (10), выпишем зависимости для компонент вектора Умова-Пойнтинга на поверхности контрольной сферы:
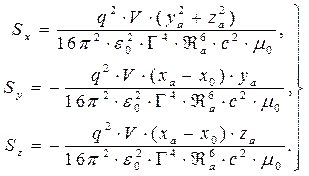 (36)
(36)
В зависимостях (36) нижний индекс «а» означает, что переменная величина рассчитывается для точки, расположенной на поверхности контрольной сферы.
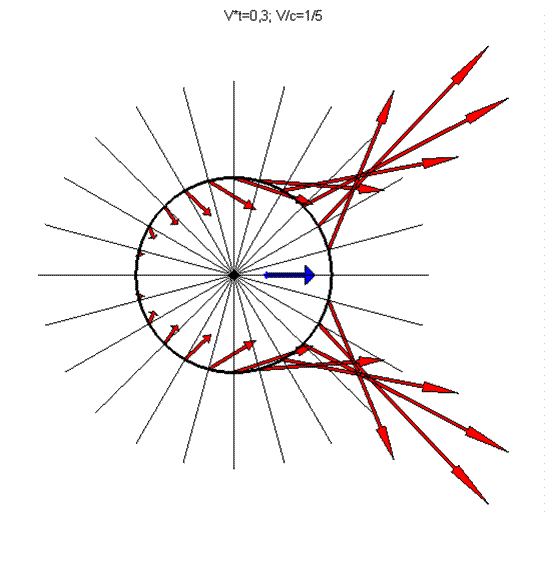

Анализируя зависимости (36), замечаем, что свойство осевой симметрии для поля объёмной плотности потока электромагнитной энергии сохраняется. На рис.7 в едином масштабе показаны векторы Умова-Пойнтинга, построенные в отдельных точках поверхности контрольной сферы радиуса а, расположенных в сечении у=0 . Электрический заряд в рассматриваемый момент времени имел продольную координату х/а =0,3. Скорость движения электрического заряда равнялась 1/5 от величины скорости света в вакууме. Лучи радиальных направлений на рис. 7 выявляют отклонение вектора Умова-Пойнтинга от направления нормали к поверхности контрольной сферы. Обращает на себя внимание тот факт, что существуют определённые направления в пространстве, для которых величина вектора Умова-Пойнтинга электромагнитного поля движущегося электрического заряда становится максимальной.
Орт нормали к элементарному участку поверхности контрольной сферы определён соотношением 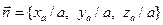 , это позволяет вычислить нормальную компоненту вектора Умова-Пойнтинга на поверхности контрольной сферы (используем сферические координаты):
, это позволяет вычислить нормальную компоненту вектора Умова-Пойнтинга на поверхности контрольной сферы (используем сферические координаты):
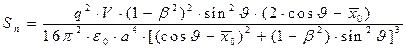 , (37)
, (37)
где 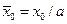 . Для тех же условий, что были использованы при построении рис.7, построены нормальные к поверхности контрольной сферы составляющие вектора Умова-Пойнтинга (рис.8). Огибающая концов рассматриваемых векторов (если её построить!) представляет собой индикатрису плотности потока электромагнитной энергии.
. Для тех же условий, что были использованы при построении рис.7, построены нормальные к поверхности контрольной сферы составляющие вектора Умова-Пойнтинга (рис.8). Огибающая концов рассматриваемых векторов (если её построить!) представляет собой индикатрису плотности потока электромагнитной энергии.
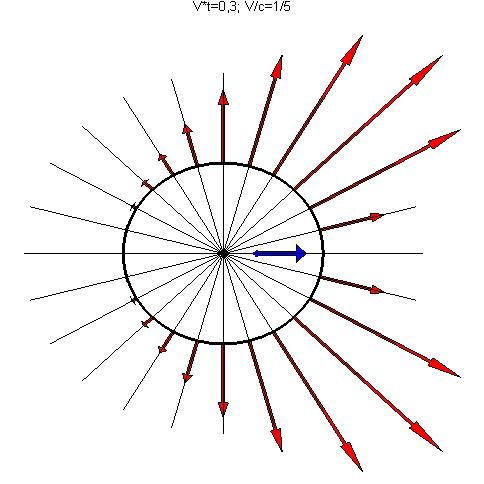
Индикатриса плотности потока электромагнитной энергии в рассматриваемом случае обладает свойством осевой симметрии.
Следует отметить, что рассматриваемое электромагнитное поле не является полем «излучения» электрического заряда: оно «жёстко» связано с движением заряда. Электромагнитное поле излучения возникает, если скорость заряда (как вектор!) является переменной величиной. В этом случае часть электромагнитного поля «отрывается» от заряда и может продолжать самостоятельное существование.
Проинтегрируем полученное выражение по поверхности контрольной сферы в сферической системе координат с учётом осевой симметрии электромагнитного поля:
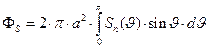 . (38)
. (38)
Закон сохранения энергии электромагнитного поля (теорема Пойнтинга) требует выполнение равенства
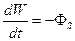 . (39)
. (39)
Поскольку аналитически показать выполнение равенства (39) не удаётся (слишком сложные выражения надо было бы интегрировать), приведём результаты численных расчётов для нескольких конкретных случаев.
Первый случай: 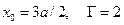 . Значения левой и правой частей равенства (39) после сокращения одинаковых сомножителей оказываются величинами порядка
. Значения левой и правой частей равенства (39) после сокращения одинаковых сомножителей оказываются величинами порядка 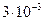 , а разность этих величин – одна единица значения
, а разность этих величин – одна единица значения 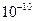 .
.
Второй случай: 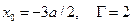 . Рассчитываемые величины поменяли знак, а величина погрешности осталась прежней.
. Рассчитываемые величины поменяли знак, а величина погрешности осталась прежней.
Третий случай: 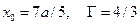 . Рассчитываемы е величины порядка
. Рассчитываемы е величины порядка 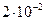 различаются только на величину
различаются только на величину 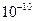 .
.
Четвёртый случай: 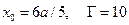 . Рассчитываемы величины порядка 0,17 в пределах точности вычислений (система символьных вычислений c 10 значащими цифрами после запятой, стандартные процедуры вычисления интегралов) не имеют различия.
. Рассчитываемы величины порядка 0,17 в пределах точности вычислений (система символьных вычислений c 10 значащими цифрами после запятой, стандартные процедуры вычисления интегралов) не имеют различия.
По-видимому, можно сделать вывод о том, что закон сохранения энергии электромагнитного поля выполняется в случае движения сосредоточенного электрического заряда с релятивистской скоростью.
Замечание. Расчёты вектора Умова-Пойнтига (соотношения (36)-(37)) могут быть выполнены, если координата 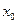 положения сосредоточенного электрического заряда в рассматриваемый момент времени не совпадает с радиусом контрольной сферической поверхности. Численная проверка соотношения (39) возможна только при условии, что точечный электрический заряд находится вне контрольного объёма: только в этом случае энергия электромагнитного поля в контрольном объёме остаётся конечной величиной. Это ограничение связано с выбором модели «точечного» электрического заряда.
положения сосредоточенного электрического заряда в рассматриваемый момент времени не совпадает с радиусом контрольной сферической поверхности. Численная проверка соотношения (39) возможна только при условии, что точечный электрический заряд находится вне контрольного объёма: только в этом случае энергия электромагнитного поля в контрольном объёме остаётся конечной величиной. Это ограничение связано с выбором модели «точечного» электрического заряда.
В который раз мы имеем возможность убедиться в глубочайшей связи между электрическим и магнитным полем, связи настолько глубокой, что электромагнитное поле представляется нам единой физической сущностью, свойства которой наиболее просто проявляются при использовании тензорного представления в 4-пространстве (пространстве-времени) СТО.
| <== предыдущая лекция | | | следующая лекция ==> |
| Тензор электромагнитного поля. | | | Акустические свойства. |
Дата добавления: 2017-09-01; просмотров: 1708;












