Что мы знаем о Теореме Пойнтинга.

Теоретически движение энергии в пространстве было изучено профессором Московского университета Н.А. Умовым (1846-1915). В его докторской диссертации «Уравнение движения энергии в телах», написанной в 1874 г., впервые введены понятия потока и плотности потока энергии (вектор Умова), объёмной плотности энергии в точке наблюдения и, главное, получено уравнение закона сохранения энергии. Десять лет спустя Дж. Пойнтинг (1852-1914) – английский физик – описал движение энергии электромагнитного поля (теорема Пойнтинга).

Теорема Пойнтинга описывает закономерности изменения во времени энергии электромагнитного поля, связанные с излучением энергии в окружающее пространство, диссипацией (джоулево тепло) и мощностью внешних сил.

Если уравнение (1) раздела 12.1

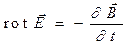
скалярно умножить на вектор 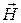, а уравнение (2) того же раздела

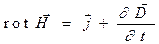
скалярно умножить на вектор 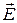и из первого уравнения вычесть второе, получим:

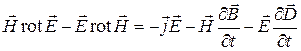. (1)

Непосредственным вычислением можно проверить, что

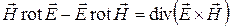. (2)

Если электрические и магнитные характеристики среды постоянны во времени 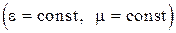, то

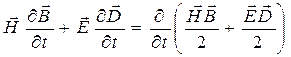. (3)

Используя полученные результаты, приходим к соотношению:

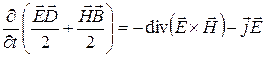. (4)

В левой части соотношения (4) стоит частная производная по времени от суммы объемных плотностей энергии электрического поля 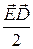(с этой величиной мы встречались в электростатике) и магнитного поля 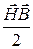(с этой величиной мы встречались в магнитостатике), а в правой части - типичный для дифференциальных законов сохранения «дивергентный член» и объемная плотность “источника” электромагнитной энергии. Для сравнения напомним, что уравнение сохранения электрического заряда не содержало объемной плотности источника зарядов.

Векторное произведение 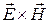играет роль плотности потока энергии (единица измерения 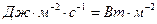). Его обозначают специальным символом 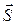и называют вектором Умова-Пойнтинга (в зарубежной литературе - вектор Пойнтинга).

Заметим, что в уравнении (4) баланса энергии электромагнитного поля вектор Умова-Пойнтинга появляется только под знаком дивергенции. Это говорит о том, что физический смысл следует приписать выражению 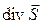, не вектору 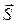непосредственно. Интерпретация величины потока вектора 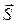через незамкнутую поверхность всегда требует осторожности (добавление к исходному вектору 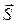произвольного вектора 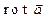не меняет величины ).

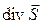С использованием уравнения (1.7) источниковый член в соотношении (4) можно переписать в форме

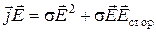, (5)

где первый член правой части - существенно положительная величина, а знак второго члена правой части зависит от взаимной ориентации векторов 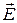и 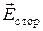. Первый член представляет собой объемную плотность джоулевых потерь, то есть объемную плотность мощности разогрева среды (Вт/м³). Второй член - это объемная плотность мощности сторонних сил, с этим членом связана возможность либо получения энергии единицей объема среды, либо совершения работы над окружающей средой.

В интегральной форме соотношение (4) имеет вид:

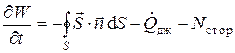, (6)

где 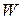- энергия электромагнитного поля, 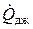- мощность джоулева тепловыделения, 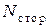- мощность сторонних сил в фиксированном объеме. Часто о соотношении (6) говорят не как о балансовом соотношении, а как о законе сохранения энергии.