Импульс электромагнитного поля.

В настоящем разделе учебного пособия обсудим понятие «импульс электромагнитного поля». При первоначальном формировании этого понятия целесообразно опереться на некоторые положения механики сплошных сред.

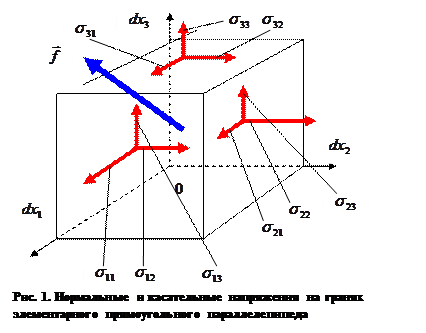
Рассмотрим элементарный прямоугольный параллелепипед (рис. 1) объёма dx₁dx₂dx_3, где оси декартовой системы координат (x,y,z) обозначены через (x₁,x₂,x₃), а его грани перпендикулярны соответствующим координатным осям.

Пусть силу, действующую на выделенный объём сплошной среды, можно записать в форме 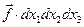. Вектор 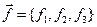в механике сплошных сред называют «объёмной силой». Правильнее говорить об объёмной плотности силы, но первое название более распространено. Помимо объёмной силы на гранях рассматриваемого параллелепипеда действуют «напряжения» 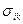, при совпадении значений индексов напряжения называют «нормальными», а при несовпадении – «касательными» напряжениями. 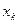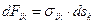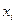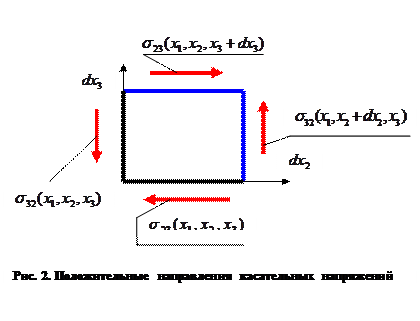Для фиксированного направления они определяют силу (не суммировать!), действующую в направлении на площадку с нормалью, параллельной координатному направлению 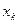. На рис.2. показаны направления сил, действующих на видимых гранях параллелепипеда, соответствующих положительным значениям соответствующих напряжений. Нормальные компоненты напряжений на противоположных гранях параллелепипеда противоположны по направлению (как и внешние нормали к поверхностям). Такое же определение принято для касательных напряжений

(рис 2).

В состоянии покоя векторная сумма всех сил, действующих на выделенный объём сплошной среды, должна равняться нулю. Рассмотрим направление :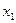

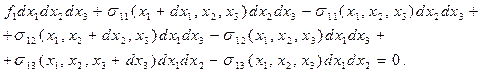(1)

После деления полученного уравнения на величину элементарного объёма 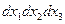получаем:

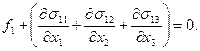(2)

Аналогично получаем и два других уравнения равновесия:

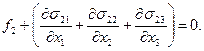(3)

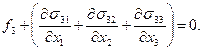(4)

Совокупность уравнений (2)-(4) можно записать в «тензорной» форме с использованием компактных индексных обозначений:

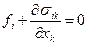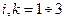, ( ). (5)

В уравнении (5) по повторяющемуся («немому») индексу выполняется суммирование в соответствии с правилом Эйнштейна. Выражение 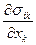(декартова система координат) называют дивергенцией тензора 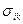. Дивергенция тензора является вектором.

В механике сплошных сред величину 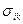( 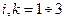) с двумя индексами называют тензором напряжений. Напомним, что наличие двух индексов ещё недостаточно для того, чтобы рассматриваемая величина (матрица!) являлась тензором: требуется выполнение определённых условий преобразования компонент этого объекта при преобразовании системы координат.

В состоянии равновесия рассматриваемого бесконечно малого объёма среды «поверхностные силы», описываемые с помощью тензора напряжений, связаны с «объёмной силой» 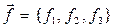системой уравнений (5). Эту систему уравнений можно записать в символическом виде:

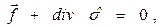(6)

где 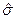- тензор с компонентами .

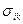В электродинамике рассматривают «тензор натяжений Максвелла»:

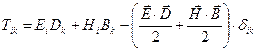. (7)

Здесь 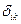- символ Кронекера, равный единице при совпадении значений индексов и равный нулю в отсутствие совпадения. Вычислим 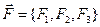- дивергенцию тензора натяжений Максвелла:

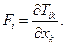(8)

Для изотропной среды, пускай неоднородной среды из выражения (7) следует:

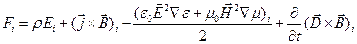. (9)

Для однородной изотропной среды в правой части выражения (9) исчезает третье слагаемое, а в случае «вакуума» ( )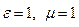

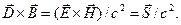
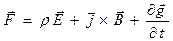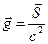, . (10)

Первые два слагаемых в правой части выражения (10) представляют собой объёмную плотность сил, действующих на свободные электрические заряды и токи проводимости. Выражение 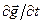представляет собой скорость изменения во времени объёмной плотности импульса электромагнитного поля, а мгновенное значение объёмной плотности импульса электромагнитного поля определяется выражением 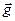в соотношении (10). Вспоминая определение вектора Умова-Пойнтинга и его размерность, установим размерность вектора 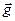: 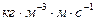. Легко видеть, что размерность объёмной плотности импульса электромагнитного поля сопадает с размерностью механической объёмной плотности потока импульса 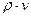, где 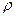объёмная плотность среды, 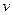- скорость элементарного объёма материальной среды.

Если в рассматриваемой среде ( 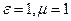) помимо объёмной плотности электромагнитных сил действует ещё и объёмная плотность механических сил 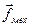, то суммарную силу, действующую на произвольный объём пространства можно записать как

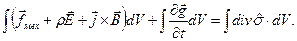(11)

Первый интеграл в соотношении (11) приводит к изменению во времени механического импульса системы 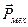, а интеграл в правой части преобразуется по теореме Остроградского-Гаусса в поверхностный интеграл и обращается в нуль при рассмотрении бесконечно большого объёма. В итоге имеем:

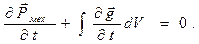(12)

Смысл соотношения (12) заключается в том, что в рассматриваемой ситуации сохраняется суммарный импульс системы, т.е. механический импульс и импульс электромагнитного поля.