Закон сохранения электрического заряда.

Закон сохранения электрического заряда неявно содержится в системе уравнений Максвелла. Рассмотрим уравнение (2) системы уравнений Максвелла (раздел 12.1):

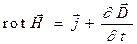. (1)

Вычислим величину дивергенции от правой и левой частей уравнения (1):

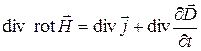. (2)

В векторном анализе известен результат (его можно проверить непосредственным вычислением!)

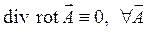. (2)

Поскольку операция вычисления дивергенции сводится к дифференцированию по пространственным координатам, то порядок вычисления частной производной по времени и вычисления дивергенции можно поменять местами, а если при этом воспользоваться уравнением (3) раздела 12.1, то получим

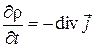(3)

- закон сохранения электрического заряда в дифференциальной форме (дивергентная форма).

Заметим, что в правой части уравнения (3), записанного в канонической форме, отсутствует объёмная плотность источника электрического заряда. Объёмная плотность электрического заряда 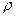в некоторой малой окрестности точки наблюдения может измениться с течением времени только в результате растекания заряда по окружающему пространству, т.е. только вследствие отличной от нуля «расходимости» объёмной плотности электрического тока проводимости.

Интегральная форма этого закона имеет вид

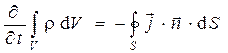(4)

или в более привычной форме записи

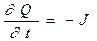. (5)

Область пространства, занятого объёмом V, не обязательно должна быть односвязной. Если в объёме V имеется поверхность, на которой расположен электрический заряд с некоторой поверхностной плотностью, возможны два описания физической ситуации. Можно считать величину объёмным зарядом, при этом сила тока 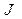определяется по «внешней» поверхности, охватывающей рассматриваемый объём, и по поверхности, охватывающей заряженную поверхность, т. е. в уравнении (5) учитываем «весь» ток, вытекающий из объёма. Вторая возможность состоит в следующем. Величину считаем суммарным электрическим зарядом системы, он состоит из объёмного заряда и поверхностного заряда. Ток 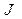в рассматриваемом случае – ток через «внешнюю» поверхность, описанную выше. Но в левой части уравнения (5) теперь необходимо учитывать и скорость изменения величины поверхностного заряда. Первая интерпретация закона сохранения заряда в интегральной форме более органично связана с дифференциальной формой (3), в то время как для обоснования второй интерпретации потребовался бы аппарат обобщённых функций.

Физический смысл полученных интегральных соотношений: в фиксированном объеме величина электрического заряда может измениться только при наличии тока (т.е. движения электрических зарядов) через замкнутую поверхность, ограничивающую этот объем. Закон сохранения электрического заряда в дивергентной форме не содержит объемной плотности источников заряда. Отсюда следует, что в классической электродинамике электрический заряд не может возникнуть и не может исчезнуть.