Соотношения на поверхности раздела двух сред.

Интегральная форма системы уравнений Максвелла справедлива для произвольного объёма пространства, заполненного материальной средой с произвольными свойствами. В настоящем разделе мы ограничимся рассмотрением конечного объёма 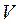, заполненного изотропной проводящей средой, обладающей свойствами поляризуемости и намагничивания. Будем считать, что объём 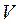ограничен замкнутой поверхностью 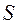. Предположим, что при переходе через поверхность 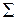, целиком лежащую внутри рассматриваемого объёма, параметры среды изменяются скачком конечной величины. Допустим, что замкнутая поверхность 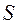и поверхность раздела сред 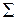, а также рассматриваемые ниже произвольные замкнутые контуры обладают достаточной степенью гладкости для существования соответствующих интегралов. Нам предстоит выяснить, каким образом связаны между собой составляющие электромагнитного поля с двух сторон поверхности 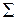- поверхности раздела двух сред.

Напомним читателю, что в настоящем пособии были рассмотрены частные случаи рассматриваемой взаимосвязи для электростатического поля и магнитостатического поля. Ниже мы рассматриваем общий, более сложный случай нестационарного электромагнитного поля.

Итак, для произвольного объёма 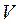, ограниченного замкнутой поверхностью 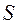, справедливы соотношения:

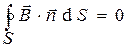, (1)

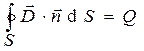, (2)

где 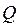- электрический заряд, величина которого определяется объёмной плотностью 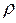стороннего электрического заряда, распределённого в объёме 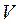, и поверхностной плотностью 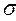стороннего электрического заряда, распределённого по поверхности раздела сред :

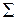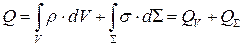. (3)

Здесь 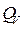- объёмный электрический заряд, 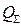- поверхностный электрический заряд.

Вторая пара интегральных соотношений системы уравнений Максвелла связывает между собой соответствующие контурные и поверхностные интегралы:

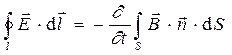, (4)

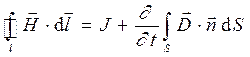, (5)

где величина “сила тока” 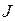определена соотношением

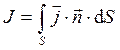. (6)

В соотношении (5) молчаливо предполагается, что на контрольной (произвольной) поверхности 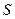, опирающейся на замкнутый контур 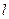, отсутствует поверхностная плотность стороннего электрического заряда. Только в этом случае величина вектора 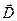может быть определена однозначно. Это предположение справедливо и для определения (6): объёмная плотность тока проводимости 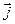не испытывает скачка на рассматриваемой контрольной поверхности .

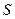Закон сохранения электрического заряда для конечного объёма 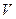, ограниченного замкнутой поверхностью 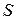, в интегральной форме имеет вид:

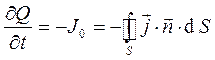. (7)

Соотношение (7) справедливо и при условии, что в рассматриваемом объёме имеет место поверхность 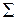с распределённым электрическим зарядом. Пусть эта поверхность окружена замкнутой поверхностью 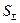, примыкающей к ней, а вектор 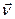является вектором внешней нормали к элементу поверхности 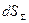по отношению к рассматриваемому объёму. Динамика изменения суммарного электрического заряда в этом случае действительно описывается соотношением (7):

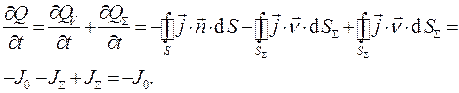
Можно показать, что для случая расположения поверхностного электрического заряда непосредственно на поверхности 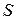в уравнении (7) величина вектора 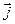должна быть вычислена как предельная величина с «внешней» стороны контрольной поверхности.

Соотношения на границе раздела двух сред для нормальных к поверхности раздела составляющих нестационарного электромагнитного поля (индукция 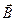магнитного поля и вектор 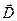электрического поля) являются следствием уравнений (1) и (2). Поскольку структура рассматриваемых уравнений одинакова, удобно провести выкладки для нормальных компонент вектора 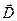в соответствии с уравнением (2). Пусть малый элемент поверхности 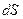принадлежит поверхности раздела двух сред. Единичный безразмерный вектор нормали 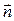к этому элементу поверхности направим в соответствии с рисунком 1. Полупространство под элементом 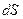будем считать первой средой, составляющие электромагнитного поля в этой среде обозначим подстрочным индексом 1. Полупространство над элементом 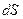будем считать второй средой, составляющие электромагнитного поля в этой среде обозначим подстрочным индексом 2. В научной литературе принято говорить, что вектор нормали 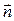направлен из первой среды во вторую. Сместим элемент поверхности 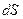вдоль направления нормали 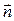на малое расстояние 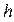и получим элемент поверхности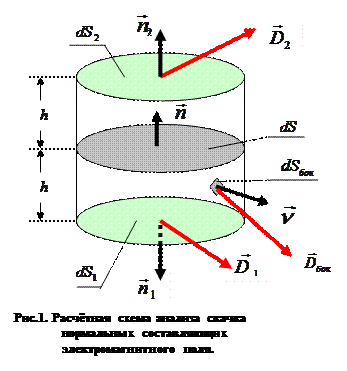 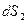. Сместим элемент поверхности 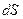в направлении, обратном направлению нормали 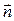, на малое расстояние 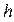и получим элемент поверхности 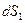. Рассмотрим малый цилиндр с основанием 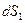и высотой 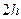, ограниченный боковой поверхностью 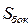. В соответствии с определением понятия «внешняя нормаль» по отношению к рассматриваемому объёму векторы 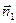- нормаль к элементу поверхност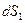и и 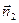- нормаль к элементу поверхности 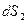- построим, как показано на рисунке 1. К малому элементу боковой поверхности 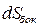также проведём единичный безразмерный вектор внешней нормали 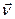. Пусть периметр контура, ограничивающего элемент 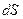, равен 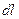. Уравнение (2) аппроксимируем соотношением:

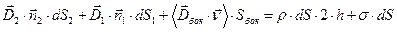. (8)

В уравнении (8) величины 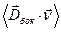и 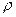являются некоторыми осреднёнными величинами, которые не превосходят соответствующих конечных максимальных значений в объёме и на боковой поверхности. По построению имеют место равенства 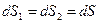. Легко видеть, что 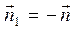, 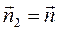и 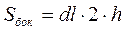. Устремляя величину 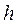к нулю и отбрасывая члены более высокого порядка малости, приходим к уравнению

.

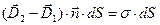В силу произвольности величины 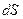справедливо условие скачка нормальных компонент вектора 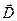при переходе через границу раздела двух сред:

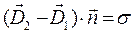. (9)

Величина скачка нормальных компонент вектора 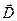при переходе через границу раздела двух сред может оказаться равной нулю (непрерывность нормальных компонент вектора 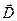) только при условии отсутствия на поверхности раздела поверхностной плотности стороннего электрического заряда:

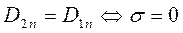. (10)

Повторяя приведённые выше рассуждения применительно к уравнению (1) относительно нормальных к поверхности раздела сред компонент вектора магнитной индукции 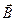с учётом того, что магнитные заряды в природе как самостоятельные субстанции физически не существуют, приходим к выводу, что нормальные компоненты индукции магнитного поля на границе раздела двух сред всегда непрерывны:

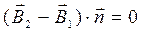. (11)

Установление взаимосвязи между касательными составляющими нестационарного электромагнитного поля, входящими в уравнения (4) и (5), начнём с рассмотрения рисунка 2. Пусть поверхность раздела сред в окрестности точки наблюдения представляет собой некий плоский элемент (на рисунке он сплошь залит серой краской) с нормалью 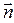, позволяющей выделить среду 1 под поверхностью раздела и среду 2 над поверхностью раздела. На поверхности раздела двух сред рассмотрим произвольное касательное направление – направление, задаваемое единичным безразмерным вектором 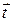. 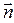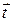Два вектора и определяют в пространстве плоскость, перпендикулярную поверхности раздела. В этой плоскости можно провести замкнутый контур 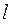, охватывающий поверхность 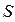, одна часть поверхности 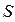расположена в среде 1, а другая – в среде 2. В соответствии с уравнением (5) нам предстоит рассмотреть циркуляцию вектора напряжённости магнитного поля 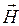по выбранному контуру с учётом того, что через поверхность 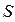текут токи проводимости с объёмной плотностью 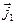в первой и объёмной плотностью 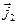во второй среде. Дифференциал силы тока проводимости определяется при этом выражением 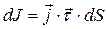, где единичный безразмерный вектор 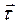перпендикулярен плоскости 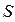и является касательным к поверхности раздела сред в точке наблюдения: 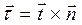. Кроме этого, по поверхности раздела могут течь поверхностные токи проводимости. Дифференциал силы поверхностного тока проводимости, текущего через поверхность 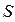вдоль поверхности раздела сред, определяется при этом выражением 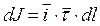. Здесь 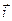- линейная плотность поверхностного тока проводимости, а положительная величина элемента длины dl рассчитывается вдоль выбранного касательного направления 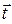. Кроме того, необходимо учесть вклад в величину рассматриваемой циркуляции скорости изменения потока вектора 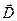через поверхность 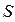, элементарный поток этого вектора равен скалярному произведению 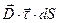. В уравнениях (4) и (5) положительное направление обхода контура 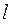и направление нормали 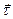к поверхности 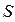согласованы правилом правого винта, как и показано на рисунке 2.

Конкретизируем геометрию контура 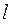. Пусть протяжённость поверхности 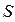вдоль направления 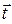составляет малую величину 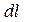, верхняя часть контура получена смещением этого отрезка на малую величину 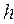по направлению нормали 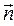, а нижняя часть контура получена смещением того же отрезка на величину 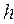по направлению, противоположному направлению нормали 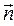. Таким образом, обе части контура 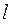, параллельные направлению нормали 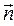, имеют протяжённость 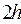. Аппроксимируем уравнение (5) соотношением:

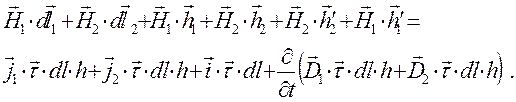(12)

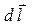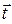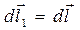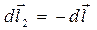Если считать вектор направленным вдоль вектора , то имеют место равенства: и . Направленные отрезк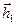и и 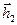(правая часть контура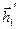) и и 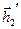(левая часть контура), протяжённость которых равна 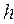, совпадают с направлением обхода контура. Скалярные произведения, которые содержат в качестве сомножителя указанные отрезки, пропорциональны малой величине 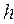и равномерно стремятся к нулю при стремлении к нулю величины 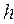. Это предположение справедливо, если напряжённость магнитного поля 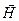, объёмная плотность тока 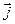, скорость изменения во времени вектора 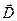остаются конечными величинами. Итак, устремим величину 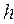к нулю и из уравнения (12) получим соотношение

.

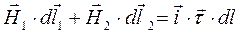Разделим полученное уравнение на величину 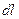с учётом очевидных соотношений , :

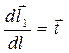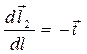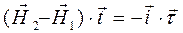. (13)

Заметим, что соотношение (13) получено с учётом определения вспомогательного вектора 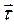в соответствии с формулой 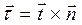, эта ориентация вектора 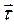показана и на рисунке 2. Если вспомогательный вектор 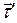определить соотношением 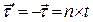, что чаще встречается в научной и учебной литературе, получим в качестве результата:

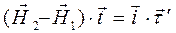. (14)

Принимая во внимание одинаковую структуру уравнений (4) и (5) и учитывая, что в природе нет магнитных зарядов, следовательно, нет и движения магнитных зарядов, в том числе по поверхности раздела сред, можно записать для касательных компонент вектора напряжённости электрического поля условие на поверхности раздела двух сред:

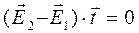. (15)

В соответствии с условием (15) касательные компоненты вектора 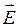при переходе через поверхность раздела сред всегда непрерывны.

Произвольный вектор напряжённости электрического поля 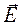в точке наблюдения можно разложить (рисунок 3) на нормальную и тангенциальную (касательную) по отношению к поверхности раздела двух сред составляющие:

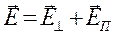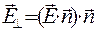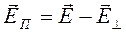, , . (16)

Следует заметить, что в условия (15) входят проекции

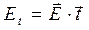, (17)

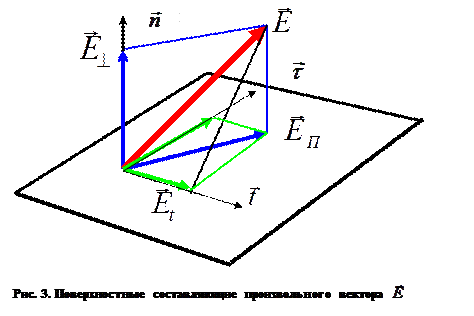что не всегда совпадает с величинами 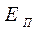. В конкретных случаях приходится учитывать различия между описанными величинами. Целесообразно термин «касательная составляющая вектора» сохранить за величиной 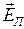, а термин «проекция вектора на касательное направление» - за величиной .

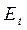Векторы напряжённости электрического поля над поверхностью раздела и под поверхностью раздела лежат в одной плоскости. Это утверждение становится очевидным, если заметить, что в частном случае из условий (15) следует

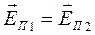. (18)

Учитывая разложение произвольного вектора на нормальную и касательную составляющие (16), полученное условие можно переписать ещё и в форме:

,

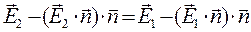или в математически эквивалентной форме

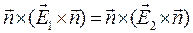. (19)

Заметим, что выражения в круглых скобках в левой и правой частях этого соотношения описывают векторы, расположенные в одной и той же касательной плоскости, эти векторы векторно умножаются на один и тот же вектор нормали, результаты этих операций могут совпасть только при условии равенства выражений в круглых скобках. Поэтому из полученного соотношения следует условие

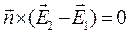. (20)

В зависимости от конкретной формулировки рассматриваемой физической ситуации условия сопряжения касательных проекций вектора напряжённости электрического поля на границе раздела двух сред можно записать в форме (15), в форме (18), в форме (19) или (20).

Физически значимым результатом проведённого анализа является, в частности, утверждение, что векторы напряжённости электрического поля над поверхностью раздела 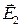и под поверхностью раздела 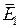и нормаль 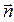к этой поверхности в точке наблюдения расположены в одной плоскости.

В отсутствие поверхностных токов проводимости на границе раздела двух сред сходными свойствами обладает и вектор напряжённости магнитного поля .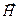

В общем случае по условию (14) величина скачка касательных компонент напряжённости магнитного поля при переходе через границу раздела сред зависит не только от величины поверхностной плотности тока проводимости, но и от выбора рассматриваемого касательного направления.

Вернёмся к рисунку 2 и соотношению (13). Если учесть очевидное определение 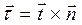, соотношение (13) можно переписать в форме:

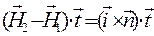. (21)

Но поскольку 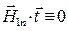, , 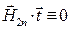из условия (21) следует:

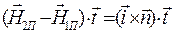, (22)

что должно быть справедливо для произвольного по направлению вектора 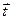. Обратим внимание читателя на то, что в уравнении (22) векторы 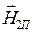, , 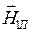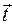и 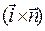лежат в одной плоскости. В этом случае из уравнения (22) следует условие:

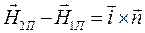. (23)

Заметим, что отмеченная выше оговорка действительно необходима: вектор 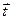не совсем произвольный вектор, его направление произвольно в касательной плоскости и он не имеет нормальной компоненты, поэтому 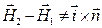, а соотношение (23) справедливо.

Перепишем соотношение (23) в «раскрытой» форме:

,

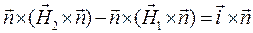Поменяем порядок сомножителей в векторных произведениях в круглых скобках левой части и в правой части этого соотношения:

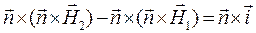
и преобразуем полученное соотношение к виду:

.

Привлекая те же соображения, что были использованы при выводе соотношения (20), получим:

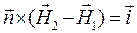. (24)

Теперь можно исследовать вопрос, лежат ли векторы 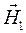, 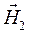и 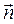в одной плоскости? Вычислим смешанное произведение этих векторов с учётом условия (24):

.

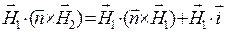Первое слагаемое в итоговом полученном соотношении тождественно равно нулю. Скалярное произведение 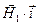может обратиться в нуль, если отсутствует поверхностный ток проводимости 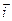, или если направление поверхностного тока 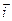перпендикулярно направлению вектора 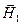. Но в последнем случае направление поверхностного тока 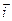перпендикулярно и направлению вектора 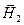. Таким образом, векторы напряжённости магнитного поля под поверхностью раздела сред и над поверхностью раздела сред и вектор нормали к элементу поверхности раздела сред только при выполнении специальных условий могут принадлежать одной плоскости.

При установлении соотношений на границе раздела двух сред для векторов поляризованности среды 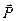и намагниченности среды 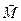необходимо воспользоваться полученными выше результатами и материальными уравнениями среды.

Обсудим условия, обусловленные действием закона сохранения стороннего электрического заряда, на границе раздела двух сред.

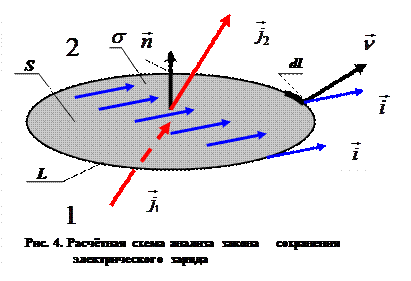Рассмотрим область S, ограниченную замкнутым контуром L, как часть поверхности раздела двух изотропных проводящих сред (рисунок 4). Пусть нормаль 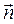к элементарному участку области S выделяет в пространстве среду 1под поверхностью раздела и среду2над поверхностью раздела. Допустим, что в обеих средах имеют место токи проводимости с объёмными плотностям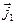и и 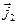, а по поверхности раздела течёт поверхностный ток проводимости с линейной плотностью 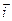. Допустим, что на поверхности раздела сред имеется сторонний электрический заряд с поверхностной плотностью 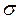. Контур L и область S поверхности раздела не изменяются и не меняют своего положения в пространстве с течением времени. Закон сохранения стороннего электрического заряда в области S в интегральной форме имеет вид:

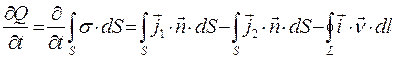. (25)

Здесь 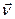- вектор нормали к элементу dl контура L. Заметим, что и вектор линейной плотности поверхностного тока проводимости 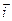, и вектор нормали 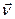к элементарному участку dl контура являются касательными к поверхности раздела сред. Физический смысл уравнения (25) очевиден: сторонний электрический заряд в рассматриваемой области поверхности может изменяться за счёт поступления электрического заряда из первой среды, за счёт вытекания заряда во вторую среду и за счёт вытекания заряда (поверхностный ток) из рассматриваемой области в остальную часть поверхности раздела.

Интеграл по замкнутому контуру 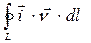в правой части уравнения (25) можно преобразовать в интеграл по поверхности:

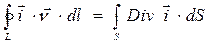. (26)

Специальный символ Div – поверхностная дивергенция – обозначает математическую операцию, символическое определение которой имеет вид:

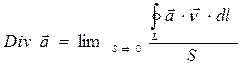. (27)

В простейшем случае декартовых координат на плоской поверхности раздела двух сред для 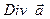имеем выражение:

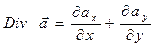. (28)

В соответствии с определение (27) с помощью поверхностной дивергенции можно математически описать явление «растекания» электрического заряда по поверхности аналогично тому, как это имеет место для «растекания» электрического заряда в объёме, описываемого с помощью дивергенции векторного поля в трёхмерном пространстве.

Учитывая приведённые определения и условия, наложенные на форму области S и замкнутого контура L, запишем уравнение (25) в форме:

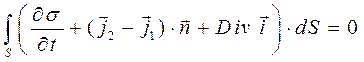. (29)

Заметим, что уравнение (29) сохраняет справедливость для любой области S. Это означает, что имеет место обращение в нуль подынтегральной функции в интеграле (29). В итоге получаем локальное условие сохранения стороннего электрического заряда на поверхности раздела двух проводящих сред:

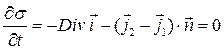. (30)

Существенным отличием формы записи закона сохранения стороннего электрического заряда на поверхности раздела сред от формы записи аналогичного закона «в объёме»

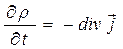(31)

является наличие поверхностной плотности «источника» стороннего электрического заряда 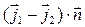. Последнее не означает возникновение «нового» электрического заряда, на самом деле на поверхность раздела двух сред перетекает заряд из прилежащего объёма.

В заключение настоящего раздела заметим, что использованные выше методические приёмы установления соотношений на границе раздела сред для составляющих нестационарного электромагнитного поля применимы не только в электродинамике. Они позволяют сформулировать соответствующие условия в механике сплошных сред (газовая динамика, механика жидкостей, теория плазмы, теория упругости, теория пластичности, теория ползучести и теория разрушения), если известны интегральные формы уравнений сохранения массы, потока импульса и энергии.