Электромагнитное поле сосредоточенного электрического заряда, движущегося в пространстве с произвольной скоростью.

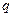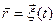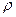В настоящем разделе электрический заряд будем считать сосредоточенным. Его мгновенное положение в пространстве опишем известной (заданной изначально) зависимостью от времени радиус-вектора . Мгновенная скорость электрического заряда, таким образом, тоже является известной зависимостью от времени . Объёмную плотность электрического заряда и плотность тока 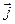в случае движения сосредоточенного заряда можно формально описать соотношениями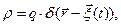 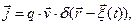где 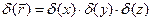- функция Дирака для случая трёх измерений. Система уравнений, которым должны удовлетворять векторный и скалярный потенциалы переменного электромагнитного поля, в случае движения сосредоточенного электрического заряда принимают вид:

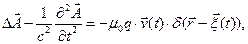
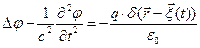. (1)

Математикам известно решение уравнений (1):

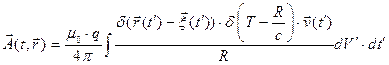, (2)

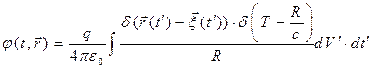. (3)

Здесь 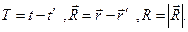После интегрирования по пространственным (штрихованным) переменным с учётом свойств - функции Дирака соотношения (2) и (3) приобретают вид:

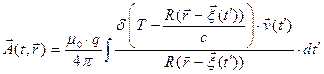, (4)

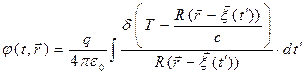. (5)

Дельта-функция Дирака от сложного аргумента может быть выражена через -функцию Дирака простого аргумента, после чего оказывается возможным выполнить интегрирование по переменной 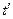. Не будем приводить подробности достаточно громоздких преобразований, их можно найти в руководствах по теоретической физике, выпишем получающийся результат:

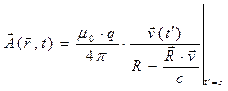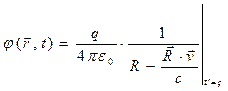, . (6)

Параметр 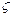в соотношениях (6) является корнем уравнения:

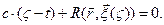(7)

Ещё раз заметим, что правые части зависимостей (6) вычисляются специфическим образом. В научной литературе зависимости (6) имеют специальное название – потенциалы Льенара-Вихерта. Они так названы в честь учёных (А. Льенар и Э. Вихерт ), которые их получили впервые.

Располагая выражениями для векторного и скалярного потенциалов (6), можно вычислить векторы напряженности электрического поля 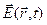и магнитной индукции 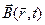. Заметим, что при этом операции дифференцирования необходимо провести по координатам точки наблюдения. Вычисления эти тоже достаточно громоздки и требуют умения, в настоящем учебном пособии они опущены, найти их можно в руководствах по теоретической физике. Окончательные зависимости имеют вид:

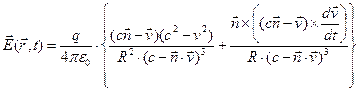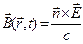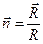, , . (8)

Заметим, что в зависимостях (8) значения 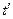заменяются параметром 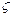в соответствии с уравнением (7).

Вектор напряжённости электрического поля, образованного движущимся сосредоточенным электрическим зарядом, имеет составляющие, параллельные вектору 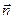, вектору скорости электрического заряда 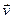и вектору ускорения электрического заряда 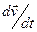. Все перечисленные векторы рассчитываются с учётом эффекта запаздывания.

Следует обратить внимание на то, что вектор индукции магнитного поля, образованного движущимся сосредоточенным электрическим зарядом, перпендикулярен вектору напряжённости электрического поля в той же точке пространства.

Второй член в фигурных скобках выражения для 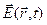обратно пропорционален первой степени расстояния. При вычислении величины вектора Умова-Пойтинга будем иметь выражение, которое содержит член, обратно пропорциональный второй степени расстояния. При вычислении потока вектора Умова-Пойтинга через поверхность сферы бесконечно большого радиуса этот член приводит к величине потока электромагнитной энергии, отличной от нуля. Это даёт нам право говорить, что движение сосредоточенного электрического заряда с ускорением ( 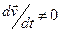) сопровождается излучением электромагнитной энергии в окружающее пространство. Интенсивность этого излучения пропорциональна квадрату ускорения сосредоточенного электрического заряда.

Движение сосредоточенного электрического заряда без ускорения (т.е. движение по прямой линии с постоянной скоростью) с течением времени приводит к изменению величины и направления напряжённости электрического и индукции магнитного поля в рассматриваемой точке наблюдения, но этот процесс не связан с излучением. В системе отсчёта, связанной с электрическим зарядом, электрическое поле является стационарным, а магнитное поле вообще отсутствует.

При движении заряда с переменной скоростью не удаётся построить инерциальную систему отсчёта, в которой этот заряд оставался бы в покое бесконечно долго. Этим объясняется принципиальное различие свойств электромагнитного поля в первом и втором случаях.