Циркуляция вектора напряжённости магнитного поля.
Пусть электрический ток 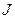 течёт по не замкнутому тонкому контуру
течёт по не замкнутому тонкому контуру 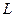 из точки 1 в точку 2 . Допустим, что требуется рассчитать циркуляцию вектора напряжённости магнитного поля
из точки 1 в точку 2 . Допустим, что требуется рассчитать циркуляцию вектора напряжённости магнитного поля 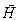 по замкнутому контуру
по замкнутому контуру 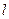 , расположенному в вакууме. Воспользуемся законом полного тока, полученным в предыдущем разделе:
, расположенному в вакууме. Воспользуемся законом полного тока, полученным в предыдущем разделе:
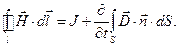 (1)
(1)
Здесь S – поверхность, натянутая на контур  ,
, 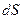 - элемент этой поверхности,
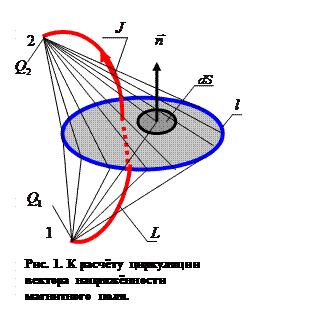
- элемент этой поверхности, 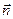 - нормаль к рассматриваемому элементу поверхности S. Рассматриваемая физическая ситуация изображена на рис. 1. Примем в качестве гипотезы, что в конечных точках 1 и 2 кривой линии
- нормаль к рассматриваемому элементу поверхности S. Рассматриваемая физическая ситуация изображена на рис. 1. Примем в качестве гипотезы, что в конечных точках 1 и 2 кривой линии 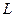 расположены сосредоточенные неподвижные электрические заряды Q1 и Q2. В квазистационарных условиях в соответствии с законом Кулона для векторов
расположены сосредоточенные неподвижные электрические заряды Q1 и Q2. В квазистационарных условиях в соответствии с законом Кулона для векторов 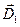 и
и 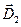 имеют место формулы:
имеют место формулы:
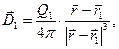
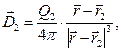 (2)
(2)
где 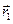 и
и 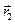 - радиус-векторы начальной и конечной точек контура
- радиус-векторы начальной и конечной точек контура 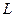 . Рассмотрим случай: контур
. Рассмотрим случай: контур 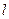 неподвижен и поверхность S неподвижна, что означает, что вектор нормали
неподвижен и поверхность S неподвижна, что означает, что вектор нормали 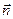 к элементу поверхности
к элементу поверхности 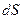 сохраняет своё положение в пространстве с течением времени. В этом случае справедливо соотношение:
сохраняет своё положение в пространстве с течением времени. В этом случае справедливо соотношение:
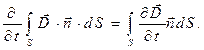 (3)
(3)
С учётом результата (3) и принципа суперпозиции перепишем уравнение (1):
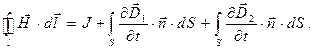 (4)
(4)
Воспользуемся законом сохранения электрического заряда
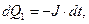
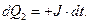 (5)
(5)
Знаки правых частей в формулах (5) определены правилом: положительным считается ток, увеличивающий положительный сосредоточенный электрический заряд. С учётом уравнений (5) получаем:
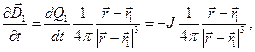
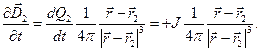 (6)
(6)
Перепишем выражение (4):
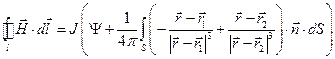 , (7)
, (7)
где 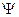 - целое число, показывающее сколько раз и в каком направлении контур
- целое число, показывающее сколько раз и в каком направлении контур 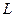 пересекает поверхность S.
пересекает поверхность S.
Поскольку для произвольного элемента поверхности и радиус-вектора 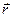 можно определить элемент телесного угла, под которым этот элемент виден из начала координат,
можно определить элемент телесного угла, под которым этот элемент виден из начала координат,
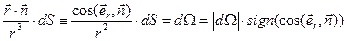 , (8)
, (8)
где
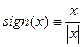 .
.
Заметим, что величина 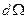 определена соотношением (8) как алгебраическая величина. Элемент телесного угла в соответствии с определением (8) считается положительным, если угол между векторами
определена соотношением (8) как алгебраическая величина. Элемент телесного угла в соответствии с определением (8) считается положительным, если угол между векторами 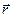 и
и 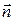 острый, и отрицательным, если он тупой. При выполнении практических расчётов важно не забывать, что площадь
острый, и отрицательным, если он тупой. При выполнении практических расчётов важно не забывать, что площадь 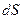 элемента поверхности
элемента поверхности 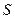 по физическому смыслу является положительной величиной.
по физическому смыслу является положительной величиной.
Зависимость (7) приобретает вид:
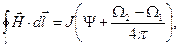
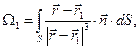
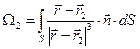 . (9)
. (9)
В окончательном выражении (9) величины 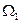 и
и 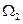 алгебраические величины телесных углов, под которыми видна поверхность S из начальной и конечной точек кривой линии L. Важно отметить, что правая часть выражения
алгебраические величины телесных углов, под которыми видна поверхность S из начальной и конечной точек кривой линии L. Важно отметить, что правая часть выражения
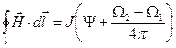
не зависит от формы поверхности S, если при этом не изменяется контур 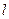 . Это обстоятельство является, по-видимому, следствием закона сохранения электрического заряда (
. Это обстоятельство является, по-видимому, следствием закона сохранения электрического заряда ( 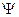 является отражением особенностей протекания тока, а
является отражением особенностей протекания тока, а 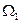 и
и 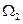 - отражением особенностей накопления и потери электрического заряда).
- отражением особенностей накопления и потери электрического заряда).
Если кривая линия, по которой течёт ток, задана параметрически
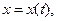
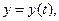
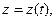 (10)
(10)
а уравнение поверхности, натянутой на контур 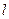 , имеет вид
, имеет вид
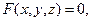 (11)
(11)
то точки пересечения являются решениями уравнения
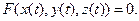 (12)
(12)
Если последовательность 
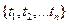 является последовательностью решений уравнения (12), остаётся только проверить, попадает ли точка
является последовательностью решений уравнения (12), остаётся только проверить, попадает ли точка 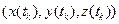 внутрь контура
внутрь контура 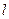 . Для каждой «правильной» точки пересечения необходимо вычислить
. Для каждой «правильной» точки пересечения необходимо вычислить 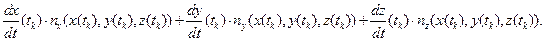 (13)
(13)
 Если эта величина положительна,
Если эта величина положительна,  увеличиваем на единицу, если отрицательна – уменьшаем на единицу. Если окажется, что уравнение (12) не имеет «правильных» решений, величина
увеличиваем на единицу, если отрицательна – уменьшаем на единицу. Если окажется, что уравнение (12) не имеет «правильных» решений, величина  принимается равной нулю. В большинстве практических случаев определение значения
принимается равной нулю. В большинстве практических случаев определение значения 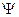 очевидно.
очевидно.
Рассмотрим некоторые типичные ситуации.
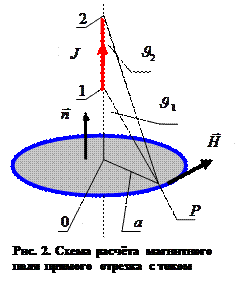
Задача 1. Рассчитать с использованием интегральной формы закона полного тока напряжённость магнитного поля H, образованного прямолинейным отрезком конечных размеров с током J в произвольной точке пространства Р, если перпендикуляр, опущенный из этой точки на продолжение прямолинейного отрезка, не принадлежит рассматриваемому отрезку. Расстояние от точки наблюдения до прямой линии равно 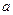 (рис. 2).
(рис. 2).
Решение. Через точку наблюдения Р проведём плоскость, перпендикулярную отрезку прямой линии с током. На этой плоскости проведём окружность радиуса 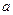
с центром в точке пересечения продолжения прямого отрезка с током и перпендикулярной ему плоскости. Для рассматриваемой физической ситуации (рис.2), очевидно, что ток не пересекает поверхность, натянутую на построенную окружность, поэтому следует принять величину 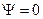 . В сферической системе координат, начало которой расположено в одной из граничных точек отрезка с током, элемент поверхности виден в пределах телесного угла
. В сферической системе координат, начало которой расположено в одной из граничных точек отрезка с током, элемент поверхности виден в пределах телесного угла
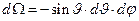 , (14)
, (14)
где 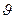 - угол между направлением тока и направлением на рассматриваемый элемент поверхности,
- угол между направлением тока и направлением на рассматриваемый элемент поверхности, 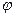 - азимутальный угол. Знак «минус» в соотношении (14) является следствием того, что по условию и угол между направлением вектора
- азимутальный угол. Знак «минус» в соотношении (14) является следствием того, что по условию и угол между направлением вектора 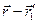 и нормалью
и нормалью 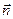 к поверхности, которая натянута на контур
к поверхности, которая натянута на контур 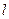 , - тупой. То же самое справедливо и для угла между направлением вектора
, - тупой. То же самое справедливо и для угла между направлением вектора 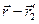 и нормалью
и нормалью 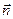 . В условиях осевой симметрии легко рассчитать телесные углы, в пределах которых виден контур, по которому необходимо рассчитать циркуляцию вектора напряжённости магнитного поля (пределы интегрирования в выражении (14) от нуля до
. В условиях осевой симметрии легко рассчитать телесные углы, в пределах которых виден контур, по которому необходимо рассчитать циркуляцию вектора напряжённости магнитного поля (пределы интегрирования в выражении (14) от нуля до 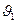 или
или 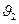 ):
):
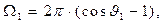
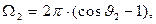 (15)
(15)
углы 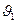 и
и 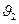 показаны на рис. 2. Ещё раз используем условия осевой симметрии задачи при записи закона полного тока:
показаны на рис. 2. Ещё раз используем условия осевой симметрии задачи при записи закона полного тока:
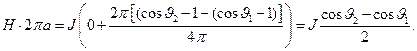 (16)
(16)
Из соотношения (4) следует результат
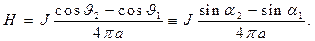 (17)
(17)
В выражении (17) углы 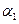 и
и 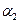 - это углы, под которыми видны начальная и конечная точки отрезка с током из точки наблюдения Р, отсчёт производится по часовой стрелке от горизонтального направления:
- это углы, под которыми видны начальная и конечная точки отрезка с током из точки наблюдения Р, отсчёт производится по часовой стрелке от горизонтального направления:
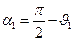 ,
, 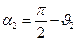 .
.
Поскольку углы 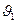 и
и 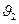 острые и выполнено очевидное условие
острые и выполнено очевидное условие 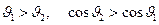 , то выражение (17) является положительным. Вектор напряжённости
, то выражение (17) является положительным. Вектор напряжённости 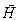 магнитного поля лежит в построенной плоскости и направлен вдоль положительного направления обхода контура. Выражение (17) совпадает с результатом расчёта величины Н с использованием закона Био-Савара-Лапласа и принципа суперпозиции.
магнитного поля лежит в построенной плоскости и направлен вдоль положительного направления обхода контура. Выражение (17) совпадает с результатом расчёта величины Н с использованием закона Био-Савара-Лапласа и принципа суперпозиции.
 Задача 2. Рассчитать с использованием интегральной формы закона полного тока напряжённость магнитного поля H, образованного прямолинейным отрезком конечных размеров с током J в произвольной точке пространства Р, если перпендикуляр, опущенный из этой точки на направление прямолинейного отрезка, принадлежит рассматриваемому отрезку. Расстояние от точки наблюдения до прямой линии равно
Задача 2. Рассчитать с использованием интегральной формы закона полного тока напряжённость магнитного поля H, образованного прямолинейным отрезком конечных размеров с током J в произвольной точке пространства Р, если перпендикуляр, опущенный из этой точки на направление прямолинейного отрезка, принадлежит рассматриваемому отрезку. Расстояние от точки наблюдения до прямой линии равно 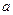 (рис. 3).
(рис. 3).
Решение. Условия задачи 2 во многом похожи на условия задачи 1. Повторяя рассуждения, использованные при решении предыдущей задачи, отметим только, что в рассматриваемом случае величина 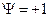 , соотношения (15) трансформируются к виду:
, соотношения (15) трансформируются к виду:
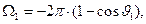
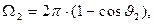 (18)
(18)
а интегральная форма закона полного тока может быть записана в виде:
|
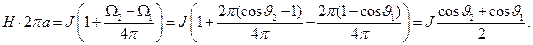 (19)
(19)
Из соотношения (19) следует:
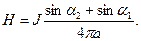 (20)
(20)
Здесь углы 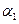 и
и 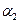 - углы между перпендикуляром из точки наблюдения к отрезку с током и направлением на начальную и конечную точку отрезка, при этом
- углы между перпендикуляром из точки наблюдения к отрезку с током и направлением на начальную и конечную точку отрезка, при этом 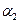 отсчитывается по часовой стрелке, а
отсчитывается по часовой стрелке, а 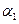 - против часовой стрелки. Для бесконечной прямой линии с током
- против часовой стрелки. Для бесконечной прямой линии с током 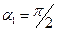 ,
, 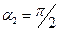 и соотношение (20) переходит в хорошо известную зависимость:
и соотношение (20) переходит в хорошо известную зависимость:
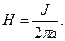 ( 21)
( 21)
Решение закончено.
Задача 3. Рассчитать с использованием интегральной формы закона полного тока циркуляцию напряжённости магнитного поля 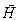 , образованного прямолинейным отрезком конечных размеров с током J, по плоской окружности радиуса
, образованного прямолинейным отрезком конечных размеров с током J, по плоской окружности радиуса 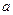 , если плоскость окружности перпендикулярна отрезку с током, а кратчайшее расстояние от прямого отрезка до центра окружности равно
, если плоскость окружности перпендикулярна отрезку с током, а кратчайшее расстояние от прямого отрезка до центра окружности равно 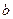 (рис.4).
(рис.4).
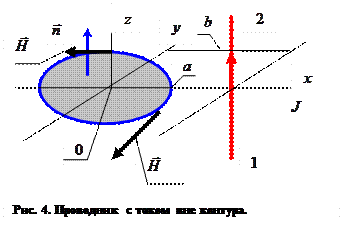 Решение. Рассматриваемая задача не обладает осевой симметрией, вычисление физических величин, входящих в выражение для интегральной формы закона полного тока, можно провести с использованием численных методов, аналитические выражения в форме квадратур полезны при этом для программирования вычислительного процесса. Решение задачи определяется зависимостями (9). Ниже приведём результаты численных расчётов циркуляции вектора напряжённости магнитного поля по окружности единичного радиуса при условии, что прямолинейный отрезок с током единичной силы отстоит от центра окружности на расстояние
Решение. Рассматриваемая задача не обладает осевой симметрией, вычисление физических величин, входящих в выражение для интегральной формы закона полного тока, можно провести с использованием численных методов, аналитические выражения в форме квадратур полезны при этом для программирования вычислительного процесса. Решение задачи определяется зависимостями (9). Ниже приведём результаты численных расчётов циркуляции вектора напряжённости магнитного поля по окружности единичного радиуса при условии, что прямолинейный отрезок с током единичной силы отстоит от центра окружности на расстояние 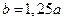 и расположен симметрично относительно плоскости окружности. Длина отрезка с током принята равной
и расположен симметрично относительно плоскости окружности. Длина отрезка с током принята равной 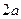 . Обозначим величину циркуляции буквой G, например. Величину G, очевидно, можно рассчитать с помощью закона Био-Савара-Лапласа и принципа суперпозиции. Для рассматриваемого случая численная величина G оказалась отрицательной и равной -0,01783. Использование интегральной формы закона полного тока, если поверхность, натянутая на окружность, является плоской, привело к результату G=-0,017797. Поменяем поверхность, натянутую на окружность. Пусть это будет пологая поверхность сферы с небольшой стрелкой сферического сегмента. Величина циркуляции при этом (
. Обозначим величину циркуляции буквой G, например. Величину G, очевидно, можно рассчитать с помощью закона Био-Савара-Лапласа и принципа суперпозиции. Для рассматриваемого случая численная величина G оказалась отрицательной и равной -0,01783. Использование интегральной формы закона полного тока, если поверхность, натянутая на окружность, является плоской, привело к результату G=-0,017797. Поменяем поверхность, натянутую на окружность. Пусть это будет пологая поверхность сферы с небольшой стрелкой сферического сегмента. Величина циркуляции при этом ( 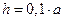 ) оказалась G=-0,017797. Для случая выпуклой сферы с большой стрелкой сферического сегмента
) оказалась G=-0,017797. Для случая выпуклой сферы с большой стрелкой сферического сегмента 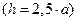 величина G=-0,018073. Приведённые результаты (при принятой точности вычислений) позволяют сделать вывод о том, что имеет место практическое совпадение рассчитываемой величины для всех расчётных схем. В интегральной форме закона полного тока форма поверхности, натянутой на контур, не существенна. Закон Био-Савара-Лапласа с принципом суперпозиции приводит к тем же результатам, что и закон полного тока.
величина G=-0,018073. Приведённые результаты (при принятой точности вычислений) позволяют сделать вывод о том, что имеет место практическое совпадение рассчитываемой величины для всех расчётных схем. В интегральной форме закона полного тока форма поверхности, натянутой на контур, не существенна. Закон Био-Савара-Лапласа с принципом суперпозиции приводит к тем же результатам, что и закон полного тока.
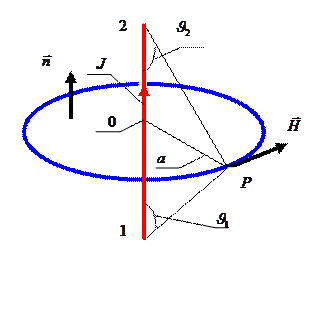
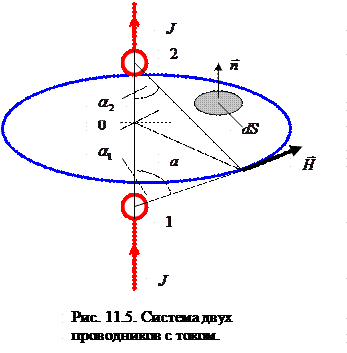 Задача 4.Две металлические сферы не касаются друг друга. По проводнику вдоль линии, проходящей через центры сфер, из бесконечно удалённой точки в точку 1 течёт ток J , увеличивая положительный заряд первой сферы. По аналогичному проводнику ток J течёт из точки 2 в бесконечно удалённую точку, уменьшая положительный заряд второй сферы (рис.5). Между сферами проводника нет. Рассчитать величину напряжённости магнитного поля в произвольной точке пространства между сферами.
Задача 4.Две металлические сферы не касаются друг друга. По проводнику вдоль линии, проходящей через центры сфер, из бесконечно удалённой точки в точку 1 течёт ток J , увеличивая положительный заряд первой сферы. По аналогичному проводнику ток J течёт из точки 2 в бесконечно удалённую точку, уменьшая положительный заряд второй сферы (рис.5). Между сферами проводника нет. Рассчитать величину напряжённости магнитного поля в произвольной точке пространства между сферами.
Решение. Для решения настоящей задачи можно воспользоваться результатами рассмотрения задачи 1 и принципом суперпозиции решений. Таким образом, получаем зависимость
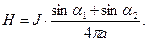 (22)
(22)
Здесь а - кратчайшее расстояние от точки наблюдения до прямой линии, соединяющей центры металлических сфер. Углы 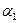 и
и 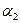 , показанные на рисунке 5, отсчитываются от вертикальной оси (линия центров сфер), причём первый угол – по часовой стрелке, а второй – против часовой стрелки.
, показанные на рисунке 5, отсчитываются от вертикальной оси (линия центров сфер), причём первый угол – по часовой стрелке, а второй – против часовой стрелки.
Отличный от нуля результат (22) было бы трудно объяснить на основе уравнений магнитостатики без привлечения понятий «ток смещения» и «полный ток». То обстоятельство, что результат (22) можно получить из закона Био-Савара-Лапласа, убеждает нас в том, что упомянутый закон справедлив и в условиях квазистационарности электромагнитных явлений.
| <== предыдущая лекция | | | следующая лекция ==> |
| Закон Био-Савара-Лапласа. Ток смещения и закон полного тока. | | | Познакомимся с параграфом |
Дата добавления: 2017-09-01; просмотров: 2538;











