Явление электромагнитной индукции.

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. КВАЗИСТАЦИОНАРНЫЕ ПРОЦЕССЫ.

Открытие явления электромагнитной индукции и установление его закономерностей сыграло основополагающую роль в формировании всего учения об электромагнитном поле и расширении области использования электричества в практических целях. Исторически первые опыты по наблюдению явления электромагнитной индукции проводились с объектами ограниченных размеров, физическое понятие « контур» применялось к конкретной электрической цепи, состоящей из проводников, конденсаторов, катушек индуктивности и источников тока. Изменения электрических параметров схемы с течением времени были медленными, «квазистационарными». Представления об «электромагнитном поле» только начинали пробивать себе дорогу в научном мире. Но и этот опыт развития учения о природе электромагнитных явлений и научные результаты описания законов электромагнитной индукции не потеряли своего значения до сих пор. Ниже обсудим закономерности явления электромагнитной индукции и рассмотрим квазистационарные процессы в простейших электрических цепях.

Явление электромагнитной индукции.

В первой трети XIX века было установлено, что взаимодействие неподвижных электрических зарядов можно описать с помощью понятия «электрическое поле», а взаимодействие движущихся электрических зарядов, т.е. токов, можно описать с помощью понятия «магнитное поле». Стало известно, что электрический ток действует на магнит (опыты Эрстеда, 1820), что магнитное поле действует на проводник с током (опыты Ампера, 1820). В 1831 г. английский ученый Майкл Фарадей (1791-1867) сделал эпохальное открытие – он открыл явление электромагнитной индукции. Принцип электромагнитной индукции в 1831 г. был известен Дж. Генри, но М. Фарадей первым опубликовал своё открытие. Это явление состоит в том, что в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего поверхность, опирающуюся на этот контур, возникает электрический (индукционный) ток. Сам по себе электрический ток возникнуть не может, следовательно, в описанной ситуации в контуре возникает электродвижущая сила (Э.Д.С.) индукции.

		Рис. 1 Схема опыта по обнаружению явления электромагнитной индукции

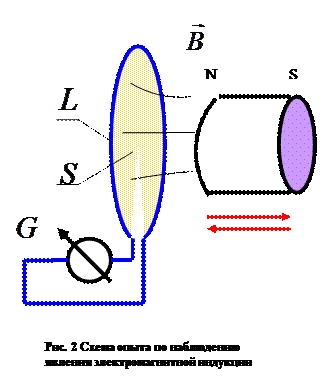
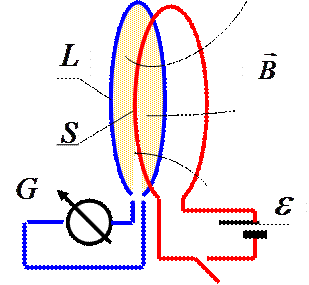
На рис. 1 и 2 показаны схемы опытов по обнаружению и наблюдению эффекта электромагнитной индукции. В первом случае стрелка гальванометра отклоняется при замыкании или при размыкании ключа в первичной электрической цепи (в установившемся режиме ток через гальванометр равен нулю). Во втором случае ток в контуре с гальванометром обнаруживается в процессе изменения положения магнита относительно контура, при этом безразлично, перемещается ли в пространстве магнит, или контур или они оба.

В результате многочисленных опытов М. Фарадей установил, что Э.Д.С. индукции пропорциональна (в современном понимании) скорости изменения магнитного потока, пронизывающего поверхность, натянутую на контур. Выбором подходящей системы единиц можно обеспечить не только пропорциональность, но и строгое равенство упомянутых величин:

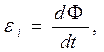
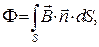(1)

где S – поверхность, натянутая на контур. Примечательно, что изменение величины магнитного потока Ф за счет изменения во времени индукции магнитного поля 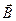, или за счет изменения взаимной ориентации векторов 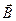и нормали 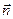или за счет изменения площади поверхности S приводит к одинаковым результатам.

Смысл закона электромагнитной индукции (1) в представлении Фарадея состоит в том, что в замкнутом проводящем ток электрическом контуре переменное во времени магнитное поле 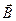в соленоиде порождает электрический ток в цепи вследствие возникновения индуцированного электрического поля 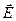. До открытия Дж. К. Максвелла, согласно которому переменное электрическое поле (даже в непроводящей среде, в отсутствие электрического тока!) порождает магнитное поле, было еще около 30 лет. Только после открытия Дж. К. Максвелла основы теории электромагнитных явлений оказались прочно установленными. Но и открытие М. Фарадея было высоко оценено современниками: известный немецкий философ Ф.В. Шеллинг в публичном выступлении на заседании Берлинской академии наук 28 марта 1832 г. оценил опыты Фарадея как основу для научного объединения механических, электрических, электрохимических, магнитных и гальванических явлений. Нечего говорить, какое значение имело открытие М.Фарадея для современного ему, да и для современного для нас состояния науки и техники. Уже в 1832 г. Дж. Генри открыл явление самоиндукции, а И. Пикси построил первый генератор переменного тока, в котором использовалось явление электромагнитной индукции. В сочетании с принципом обратимости электрических машин (Э.Х. Ленц, электрическая машина может работать как двигатель или как генератор) это достижение в скором времени обеспечило стремительное развитие электротехники, и если XIX век был «веком пара», то ХХ век по праву называют «веком электричества». Всё это просто поражает воображение, особенно если вспомнить, что первая батарейка построена А. Вольта в 1799 г., а закон Ома, сегодня известный каждому школьнику, открыт только в 1826 г.

В 1833 г. Э.Х.Ленц (1804-1865) сформулировал «правило Ленца», согласно которому Э.Д.С. индукции вызывает ток такого направления, чтобы препятствовать причине его возникновения. Сегодня это правило обосновывают несколькими путями: и с помощью понятия “устойчивая термодинамическая система” (принцип Ле Шателье-Брауна), и с помощью электромеханических методов (сила Ампера, работа по перемещению проводника с током в пространстве).

Интересно отметить некоторые исторические подробности открытия явления электромагнитной индукции. Майкл Фарадей был учеником английского химика Гемфри Дэви (1778-1829). Стиль его собственных работ был описательным, «химическим»: он не использовал даже простейших математических формул или уравнений. Основное уравнение Э.Д.С. электромагнитной индукции в форме (1) в трудах М.Фарадея не содержится. Д.К.Максвелл, изучив труды Фарадея, был поражён возможностью математического описания идей Фарадея. Правда, сделать это было под силу только гениальному учёному. Закон электромагнитной индукции Максвелл записал в форме уравнения:

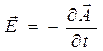. (2)

Строго говоря, и это уравнение является адаптацией уравнения Максвелла к современным обозначениям с учётом выбора системы единиц физических величин СИ. Если учесть определение векторного потенциала 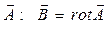и вычислить ротор от обеих частей уравнения Максвелла (2), можно получить дифференциальную форму закона электромагнитной индукции:

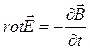. (3)

Заметим, в последующих разделах настоящего курса это будет показано, что напряжённость нестационарного электрического поля связана с потенциалами нестационарного (переменного во времени) электромагнитного поля определением:

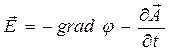. (4)

Первое слагаемое в правой части рассматриваемого уравнения при вычислении ротора тождественно обращается в нуль. Если условно разделить напряжённость электрического поля на «потенциальную» и «вихревую» части, то Э.Д.С. электромагнитной индукции зависит только от «вихревой» составляющей напряжённости. Таким образом, исходное уравнение Максвелла (2) применимо только для установления закона электромагнитной индукции. Если Э.Д.С. индукции представить в форме интеграла по замкнутому контуру от индуцированной напряженности электрического поля 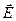, то «правильное» соотношение для закона Фарадея с учетом правила Ленца приобретет форму

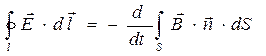. (5)

Здесь положительное направление обхода контура (ориентация элемента длины 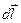контура) и направление нормали 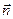к элементу площади поверхности dS (и для совокупности элементов dS) связаны между собой правилом правого винта (иначе, с конца вектора 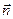положительное направление обхода контура – против часовой стрелки; еще иначе, если голова человека ориентирована в пространстве по направлению 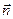, то положительным считается такое направление движения, при котором область, ограниченная контуром, остается слева).

В некоторых случаях закон электромагнитной индукции можно использовать в форме

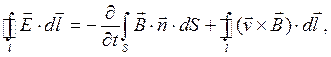(6)

где вектор 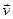- скорость смещения во времени элемента контура 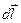. Форма (6) в явном виде учитывает возможность изменения геометрии или местоположения контура l, при этом частная производная от магнитного потока Ф вычисляется при «замороженном» состоянии контура. Можно говорить, что первый член правой части закона (6) обусловлен скоростью изменения магнитного потока во времени через поверхность, натянутую на «замороженный» контур, а второй – деформацией и смещением контура в «замороженном» магнитном поле. Интересно, что соотношение (6) можно записать в дифференциальной (локальной) форме, если предположить, что 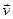- скорость частичек среды, в которую «вморожен» контур: если в соотношении (6) скорость 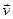- определена только для точек контура, то теперь мы предполагаем, что 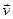определена и для точек поверхности S. В этих условиях справедливо уравнение:

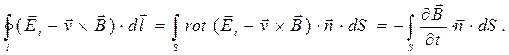(7)

При записи соотношения (7) использована математическая теорема Стокса. Из соотношения (7) в силу произвольности выбора поверхности S получаем:

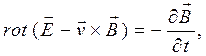(8)

где 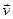- вектор скорости среды. Для неподвижной среды ( 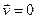) уравнение (8) переходит в уравнение (3) - уравнение электромагнитной индукции в дифференциальной форме. Из уравнения (3) следует, что в переменном магнитном поле электрическое поле перестает быть потенциальным, как это понималось в электростатике.

Заметим, что выражение (8) может дать повод говорить о возможности введения величины 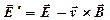, которую можно было бы интерпретировать как напряженность электрического поля в движущейся системе координат. Строго говоря, это не совсем так. В заключительной части курса будет показана степень приближенности уравнения электромагнитной индукции при переходе в другую инерциальную систему отсчета.

Вернемся к рассмотрению закона электромагнитной индукции Фарадея с учетом правила Ленца:

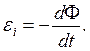(9)

Для относительно «медленных» переменных процессов можно воспользоваться определением индуктивности:

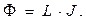(10)

Соотношение (9) с учетом определения (10) принимает вид:

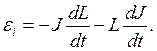(11)

Формула (11) записана с учетом возможного изменения величины индуктивности L в переменном процессе. Это может происходить при изменении размеров контура или его ориентации, или при изменении магнитных свойств среды. В последнем случае справедлива цепочка соотношений:

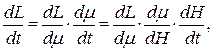(12)

где 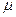- магнитная проницаемость среды, Н – напряженность магнитного поля.

В более простом и чаще встречающемся случае (неподвижный соленоид без ферромагнитного сердечника) величина L является постоянной величиной. Соотношение (9) при этом принимает форму, известную из элементарного курса

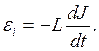(13)

Определение Э.Д.С. индукции (13) можно использовать при расчете переменных процессов в сложных цепях электрического тока. Предполагается, что правила Кирхгофа остаются в силе и в условиях применимости соотношения (13). Правило использования соотношения (13) состоит в следующем: Э.Д.С. индукции на участке цепи с индуктивностью L направляют по току J, направление которого предварительно задано произвольно. Сумма Э.Д.С. по замкнутому контуру включает в себя и Э.Д.С. индукции, определенную соотношением (13). После решения задачи выясняется истинное направление тока на рассматриваемом участке и истинное направление Э.Д.С. индукции.

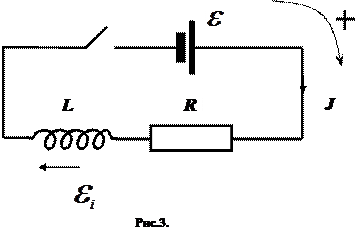
Рассмотрим простую электрическую схему, включающую в себя источник питания 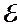, сопротивление R, индуктивность L и ключ управления (Рис. 3). Начальное состояние схемы – ток в цепи равен нулю. В этот момент замыкают ключ. Предполагаем, что положительное направление обхода выбрано по часовой стрелке, направление Э.Д.С. совпадает с направлением обхода, направление тока J совпадает с направлением обхода. Э.Д.С. индукции направляем «по току». Второе правило Кирхгофа записываем в форме:

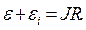(14)

Используя соотношение (13), перепишем уравнение (14):

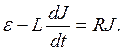(15)

Примеры использования второго правила (закона) Кирхгофа с учетом явления электромагнитной индукции при исследовании квазистационарных явлений в линейных электрических цепях рассмотрены в следующих разделах настоящего учебного пособия.

Ниже рассмотрим уравнение (15). Умножим обе части этого уравнения на величину J:

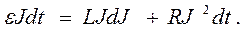(16)

Второй член правой части уравнения (16) представляет собой количество тепла, выделившегося в цепи по закону Джоуля-Ленца за время dt, левая часть уравнения (16) представляет собой работу источника тока за то же время. Член LJdJ представляет собой приращение «магнитной» энергии в системе:

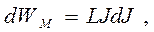(17)

что приводит к известному соотношению:

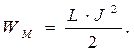(18)

Если рассматриваемая электрическая схема содержит соленоид с ферромагнетиком, то в переменном процессе необходимо учесть изменение индуктивности элемента цепи:

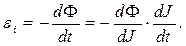(19)

В этом случае уравнение второго правила Кирхгофа имеет вид:

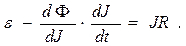(20)

Поскольку величина dФ/dt в конечном итоге определяется величиной силы тока J, то решение уравнения (20) с однородным начальным условием для силы тока (и условием 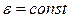) может быть сведено к квадратуре:

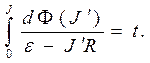(21)

По соотношению (21) можно рассчитать время t, необходимое для достижения величины силы тока J. Дифференциал dФ(J) в выражении (21) зависит параметрически от геометрии ферромагнитного сердечника и кривой намагничения

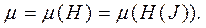(22)

Если уравнение (20) умножить почленно на силу тока J, то можно заключить по аналогии с анализом уравнения (17), что дифференциал магнитной энергии системы имеет вид:

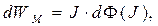(23)

а выражение для магнитной энергии определено зависимостью:

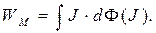(24)

В заключение отметим, что для достаточно быстропеременных процессов необходимо учитывать зависимость кривой намагниченности от частоты.