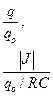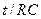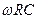Квазистационарные процессы в простейших электрических цепях.

Ниже рассмотрим нестационарные электромагнитные явления в электрических цепях, которые содержат ёмкость, или индуктивность или то и другое вместе, причем геометрические размеры этих элементов малы по сравнению с характерной длиной электромагнитной волны. Иначе, рассмотрим достаточно медленные процессы, в которых характерное время процесса значительно превышает период колебаний электрических величин в электромагнитной волне распространения возмущения. В этих случаях распределение электрических величин в конденсаторе или в катушке индуктивности можно считать квазистационарным: поле меняется одновременно во всём объёме конструктивного элемента. Интересно отметить, что в рассматриваемых случаях частично сохраняются основные закономерности цепей постоянного тока и появляются качественно новые особенности протекания физических явлений. Их изучению посвящен настоящий раздел.

10.2.1.RC – цепочка.

Рассмотрим электрическую схему (рис. 1) которая включает в себя активное сопротивление 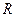и последовательно соединенный с ним конденсатор ёмкости 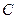. Смысл понятия «активное сопротивление» будет выявлен ниже при рассмотрении периодического гармонического процесса в рассматриваемой RC-цепочке. Допустим, что между входными клеммами RC-цепочки приложено

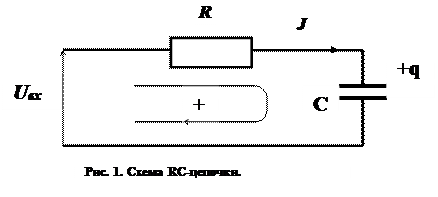
входное напряжение 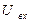. Для произвольно выбранного положительного направления обхода электрического контура, положительного направления силы тока в цепи и произвольно выбранной положительной полярности обкладок конденсатора, показанных на рис.1, имеем:

. (1)

Физический смысл уравнения (1) очевиден: электрический ток (движение положительных зарядов) увеличивает положительный электрический заряд 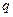выбранной обкладки конденсатора. Для выбранной полярности обкладок конденсатора падение напряжения на его обкладках описывается выражением:

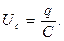(2)

«Направление» падения напряжения совпадает с положительным направлением обхода контура (потенциал верхней пластины больше потенциала нижней пластины конденсатора). В рассматриваемых условиях второй закон Кирхгофа можно записать в форме:

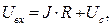(3)

соотношение (3) справедливо для мгновенных значений всех входящих в него величин. Обратим внимание читателя на то, что входное напряжение в уравнении (3) выступает в роли внешней электродвижущей силы (ЭДС).

Заметим, что «полярность» обкладок конденсатора имеет важное значение и для записи закона сохранения электрического заряда (уравнение (1)), и для записи второго закона Кирхгофа. Последнее становится очевидным, если конденсатор уподобить батарейке, полагая «плюс обкладки» подобным «плюсу батарейки». ЭДС такой «батарейки» равна разности потенциалов на обкладках конденсатора . Рассматриваемую ЭДС необходимо записать в левой части второго закона Кирхгофа с учётом направления действия ЭДС и положительного направления обхода контура. Для контура, показанного на рис.1, вместо уравнения (3) можно записать:

.

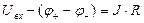Если перенести разность потенциалов обкладок конденсатора в правую часть этого уравнения, получим аналог уравнения (3).

С учетом зависимостей (1) и (2) перепишем уравнение (3):

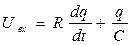(4)

и придадим полученному уравнению каноническую форму:

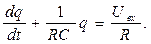(5)

Общее решение дифференциального уравнения (5) имеет вид:

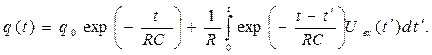(6)

В соответствии с выражением (6) имеем:

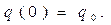(7)

В начальный момент времени величина электрического заряда конденсатора определяется величиной 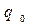. С помощью соотношений (1) и (2) по зависимости (6) можно рассчитать законы изменения во времени силы тока в цепи и падение напряжения на активном сопротивлении и на обкладках конденсатора.

Разрядка конденсатора. В частном случае разрядки конденсатора входные клеммы RC-цепочки замкнуты, 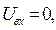при этом процесс изменения во времени электрического заряда конденсатора описывается уравнением

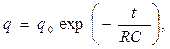(8)

где 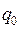- заряд конденсатора в начальный момент времени.

Заметим, что зависимость силы тока от времени в рассматриваемом случае

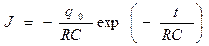(9) отрицательна, это свидетельствует о том, что действительное направление силы тока в цепи не совпадает с выбранным положительным направлением обхода

контура.

Рис.2. Процесс разрядки конденсатора.

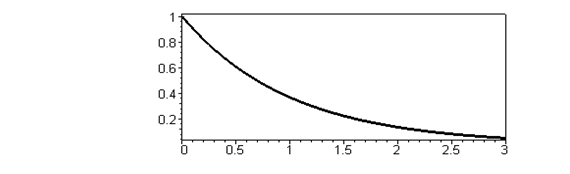
В соответствии с выражениями (8) и (9) величина заряда конденсатора 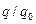и абсолютная величина силы тока в цепи 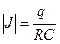монотонно убывают с течением времени, но в нуль обращаются только при его бесконечном значении (рис. 2).

Зарядка конденсатора. В частном случае зарядки конденсатора с помощью источника постоянного во времени напряжения общее решение уравнения (5) можно записать в форме:

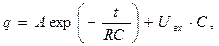(10)

где - произвольная постоянная. Если в начальный момент времени конденсатор уже имел электрический заря величины 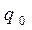, то необходимо потребовать выполнения условия

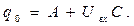(11)

В итоге получаем решение:

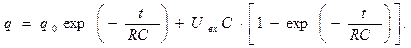(12)

Интересно отметить, что процесс зарядки конденсатора в соответствии с полученным решением можно рассматривать как сложный процесс: процесс убывания начального заряда конденсатора («разрядка» конденсатора) и процесс зарядки конденсатора, не заряженного в начальный момент времени. Чаще всего рассматривают случай 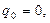при этом из зависимости (12) можно получить

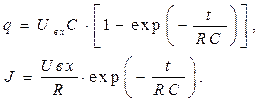(13)

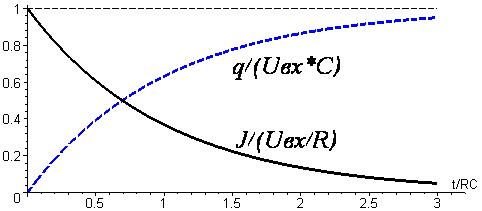
На рис. 3. приведены графики изменения относительной величины тока зарядки 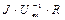и относительной величины текущего заряда конденсатора 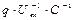с течением времени.

Для полученных зависимостей характерным является свойство «насыщения»: приращение величины заряда конденсатора в единицу времени монотонно убывает с течением времени. Заметим, что и в процессе зарядки и в процессе разрядки конденсатора в составе RC-цепочки важную роль играет величина произведения RC – характерного времени переходного процесса: если 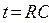, то относительное изменение заряда конденсатора составляет , т.е. величина заряда изменяется в « 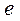» раз. В практических прикидочных расчетах обычно полагают, что время переходного процесса в RC-цепочке составляет .

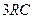Для зависимостей изменения электрических величин в RC-цепочке показателен асимптотический характер процесса, мгновенная разрядка или зарядка конденсатора в составе RC-цепочки физически невозможна. Последнее не означает, что всегда необходимо учитывать динамику процессов в RC-цепочке. Временем переходного процесса можно пренебречь при анализе сложной электрической схемы, если характерное время процесса для системы в целом значительно больше времени переходного процесса в RC-цепочке.

RC-цепочка в цепи переменного тока. Рассмотрим более подробно физические процессы в RC-цепочке при условии, что на её входные клеммы подано гармоническое напряжение

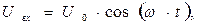(14)

где 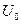- положительная постоянная величина, 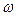- круговая частота, равная 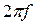, 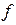при этом равна 1/T, т.е. равна обратной величине периода колебаний. Обычно, когда говорят о частоте переменного тока, имеют в виду «циклическую» частоту колебаний .

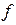Математический анализ динамических процессов, обладающих гармоническим характером изменения переменных, удобно проводить с использованием комплексных переменных

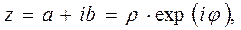
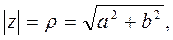
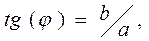
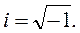(15)

Рассматривая известную формулу Эйлера

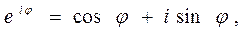(16)

замечаем, что выражение (14) представляет собой действительную часть комплексного выражения

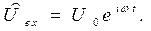(17)

Принимаем, что «на входе» RC-цепочки задано напряжение соотношением (17) с условием, что физический смысл сохраняется за действительными частями всех последующих комплексных величин. Далее, рассмотрим процесс установившихся вынужденных колебаний физических величин в RC-цепочке, влиянием начальных параметров процесса при этом пренебрегаем (математики в таких случаях говорят о задаче без начальных условий).

Полагая, что решение уравнения (5) при выполнении условия (17) имеет вид

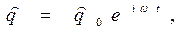(18)

где «амплитуда» 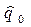не зависит от времени 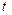, но может быть комплексной величиной, подставив соотношение (18) в уравнение(5), приходим к следующему уравнению

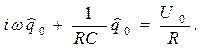(19)

Решением полученного уравнения является выражение

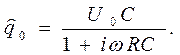(20)

Запишем выражение (20) в экспоненциальной форме

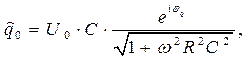
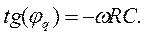(21)

Полученный результат используем в выражении (18) при расчете мгновенного комплексного значения заряда конденсатора:

(22)

Комплексное значение амплитуды колебания физической величины определяет физическую амплитуду колебаний 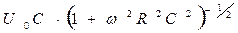-модуль комплексной амплитуды в зависимости (22) и соответствующую начальную фазу колебаний (угол 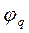). Обе эти характеристики процесса колебаний являются действительными величинами с очевидным физическим содержанием.

Соотношения (21) и (22) с использованием закона сохранения электрического заряда (1) позволяют вычислить комплексную амплитуду силы тока

(23)

комплексную амплитуду падения напряжения на обкладках конденсатора

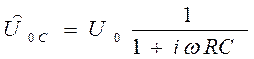(24)

и комплексную амплитуду падения напряжения на активном сопротивлении R

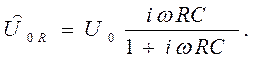(25)

Легко проверить, что второй закон Кирхгофа выполнен для комплексных амплитуд соответствующих физических величин

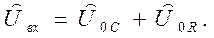(26)

Обратим внимание читателя на то, что из условия равенства комплексных выражений следует условие равенства их действительных частей. В рассматриваемом случае мы получили «проверку» того, что второй закон Кирхгофа выполняется для мгновенных значений падений напряжений в RC-цепочке.

В выражении для комплексной амплитуды падения напряжения (24) на обкладках конденсатора избавимся от мнимой части в знаменателе

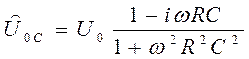(27)

и перепишем полученное выражение через модуль комплексной величины и фазовый угол:

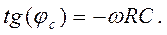, (28)

Таким образом, приходим к зависимости комплексной величины падения напряжения на обкладках конденсатора от времени

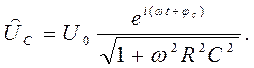(29)

Действительная часть выражения (29) согласно формуле Эйлера имеет вид

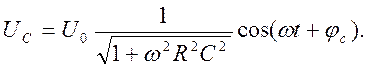(30)

Действующее (эффективное, измеряемое вольтметром) падение напряжения на обкладках конденсатора определяется зависимостью

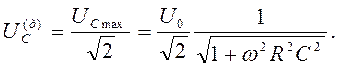(31)

Если учесть, что действующее (эффективное, измеряемое вольтметром) входное напряжение равно 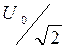, получаем окончательно для эффективных величин:

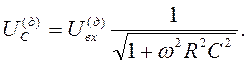(32)

Аналогичная процедура применительно к соотношению (25)приводит к зависимостям

(33)

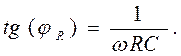(34)

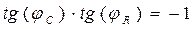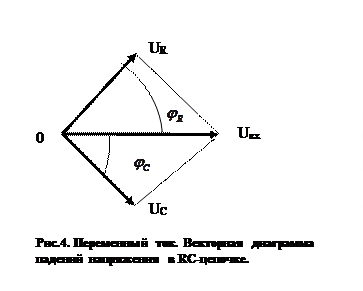
Заметим, что имеет место соотношение . Это свидетельствует о том, что мгновенные фазы колебаний падения напряжения на обкладках конденсатора и на активном сопротивлении различаются на угол 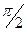(в радианах). На векторной диаграмме (рис. 4) соответствующие векторы падений напряжения взаимно перпендикулярны.

Следствием зависимости (33) является формула

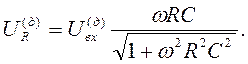(35).

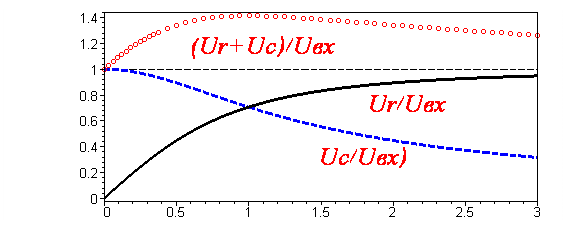
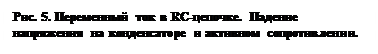
На рис. 5 показаны графики зависимостей измеряемых напряжений (относительные величины) в RC-цепочке от произведения (эта величина пропорциональна отношению характерного времени для процессов в RC-цепочке к периоду гармонического колебания входного напряжения). Верхняя кривая рисунка – относительная величина суммы эффективных напряжений на конденсаторе и активном сопротивлении – превышает единицу (относительная величина эффективного напряжения на входных клеммах RC-цепочки). Получается, что сумма падений напряжений в цепи больше, чем входное напряжение. Налицо «нарушение» правил Кирхгофа. Это нарушение кажущееся, оно возникает при попытке использовать действующие напряжения (т.е. модули физических величин) вместо комплексных значений, учитывающих сдвиг начальных фаз гармонических колебаний этих величин.

Заканчивая рассмотрение процессов вынужденных гармонических колебаний физических величин в RC-цепочке, отметим следующие закономерности описываемого явления.

1. RC-цепочка с идеальным конденсатором не проводит постоянный ток. В этом случае круговая частота входного напряжения равна нулю ( 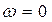), сила тока в цепи обращается в нуль ( 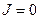), падение напряжения на активном сопротивлении обращается в нуль ( 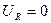), падение напряжения происходит только на обкладках конденсатора ( ).

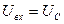2. При больших значениях безразмерного параметра 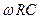, характеризующего отношение характерного времени протекания динамических процессов в RC-цепочке к периоду вынуждающего воздействия, конденсатор не оказывает существенного (заметного) сопротивления переменному току, падение напряжения, в основном, происходит на активном сопротивлении.

3. Сумма измеряемых (действующих, эффективных) падений напряжения на активном сопротивлении и на обкладках конденсатора не равна измеряемому (действующему, эффективному) напряжению, приложенному к входным клеммам RC-цепочки.