Основная волна прямоугольного волновода

Свойства волны. Как уже отмечалось, при а > b основной волной прямоугольного волновода является волна Н10. Она имеет наибольшую критическую длину волны, равную 2а. На заданной частоте размеры поперечного сечения волновода, при которых возможна передача энергии по прямоугольному волноводу, для этой волны можно выбрать наименьшими. При этом волновод будет иметь наименьшие массу, габариты и стоимость.

Полагая в (17) m = 1 и n = 0 и учитывая формулы (16), получаем следующие выражения для составляющих комплексных амплитуд векторов Ε и Η в случае волны Н10.

E_my =-i(ωμπ/a)Η_0z sin(πx/a)exp(-iß₁₀z),

H_mx = i(ß₁₀π/a) H_0z sin(πx/a)exp(-iß₁₀z),

Н_mz = Н_0z соs(π х/а)ехр(-iß₁₀z),

E_mx = E_mz = 0, Н_0y = 0,

где

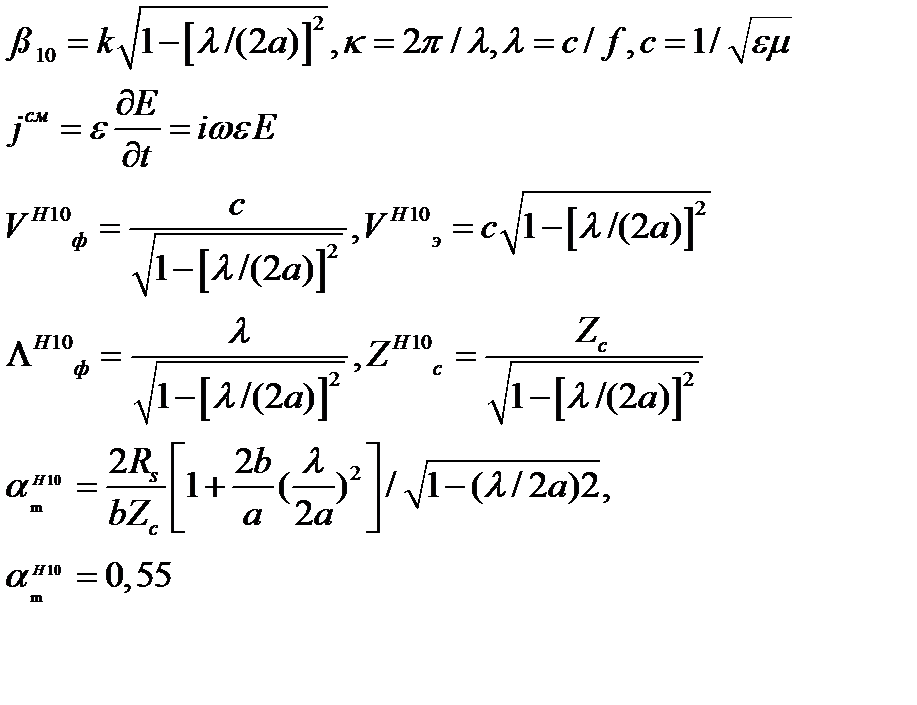(18)

Структура поля волны Н10, построенная в соответствии с формулами (18), показана на рис.9 и 12. Остановимся на картине распределения поля волны Ню в плоскостях, параллельных широким стенкам волновода.

Рис 12

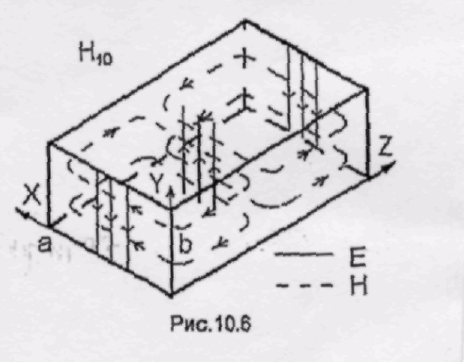Согласно уравнениям Максвелла замкнутые линии магнитного поля должны охватывать токи проводимости или токи смещения. В волноводе замкнутые линии магнитного поля пронизываются токами смещения. В случае волны Н10 (см. рис.12) линии магнитного поля охватывают токи смещения, текущие между широкими стенками параллельно оси У. В распространяющейся волне максимальная плотность тока смещения получается в центре замкнутых магнитных силовых линий, где напряженность электрического поля равна нулю. Это следует из того, что вектор плотности тока смещения 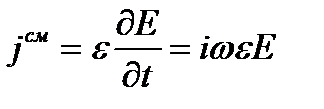и, следовательно, сдвинут по фазе относительно вектора напряженности электрического поля на угол π/2, т.е. расстояние между максимумом плотности тока смещения и максимумом напряженности электрического поля вдоль оси Ζ в фиксированный момент времени равно Λ/4.

Фазовая скорость νф, скорость распространения энергии vэ, длина волны в волноводе Λ и характеристическое сопротивление Zc в случае волны Н10 вычисляются по формулам

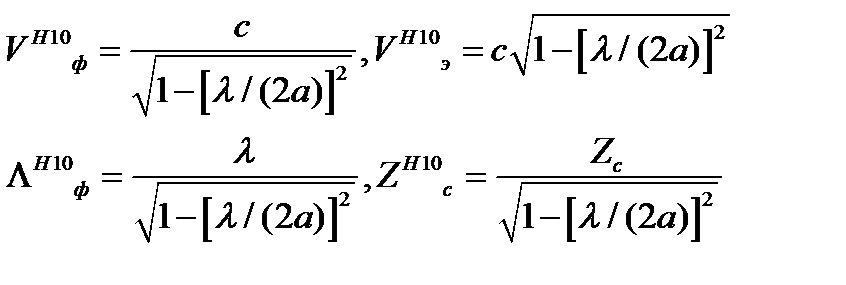(19)

Рис 14

Рис 13

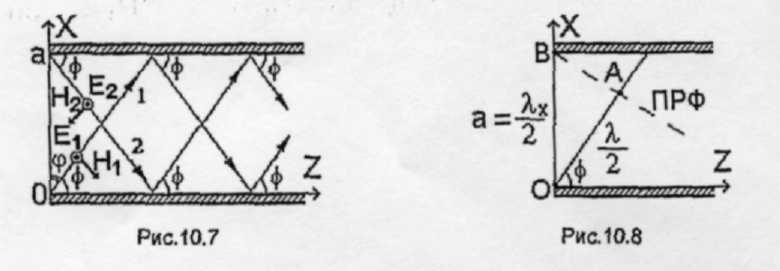
Можно представить волну Н10 в виде суперпозиции парциальных ТЕМ-волн.

Поле волны Н10 не зависит от переменной у. Следовательно, поля парциальных волн также не должны зависеть от у, т.е. парциальные ТЕМ-волны должны распространяться, отражаясь от боковых (х = 0 и x = а) стенок волновода.

Пусть парциальная волна распространяется под углом φ к оси Ζ (волна 1 на рис.13). Комплексная амплитуда вектора напряженности электрического поля этой волны Em1 определяется выражением

E_m1 = у₀ A exp[-ik(x sin φ + z соs φ)], (20)

где А - некоторая (в общем случае комплексная) постоянная. Электрическое поле волны Н10 имеет пучность на плоскости x = а/2 и симметрично относительно этой плоскости. Поэтому должна существовать еще одна парциальная ТЕМ-волна распространяющаяся, как показано на рис.13. Комплексная амплитуда напряженности электрического поля этой волны равна Ё_m2, причем │Ёm2│= │Ёm1│= А. Для образования пучности электрического поля в плоскости x = a/2 необходимо, чтобы векторы Ёm1 и Ёm2 при x = а/2 складывались синфазно. Для этого достаточно, например, чтобы фаза вектора Ёm2 в точке (а, 0, 0) совпадала с фазой вектора Ёm1 в точке (0, 0, 0). С учетом данного условия вектор

Ё_m2 =y₀А ехр (-ik [(a-х) sin φ + z соs φ]). (21)

Для определения угла φ учтем, что на поперечном размере а широкой стенки волновода должна укладываться половина длины волны λΧ1 а на отрезке ОА - половина длины волны ТЕМ (λ/2). Из треугольника ОАВ (см. рис.14) следует равенство sin φ =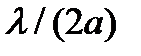

При этом kа sin φ = (2π/λ) λ/(2a) = π, kх sin φ = πx/a, и полное электрическое поле определяется выражением

Ёm = Ё_m1 +Ё_m2 = - у₀2iA sin (πx/a) exp (-iß₁₀z). (22)

Полученный результат отличается от выражения для Ёmy в формуле (17) лишь постоянным коэффициентом, что несущественно, так как формулы (17) были найдены с точностью до произвольного постоянного множителя. Аналогично вычисляются составляющие Нmx и Нmz. Они отличаются от соответствующих выражений в (17) лишь тем же постоянным множителем.

По мере повышения частоты (уменьшения λ) уменьшается угол φ и, следовательно, тем меньше по абсолютной величине становится продольная составляющая Нmz по сравнению с поперечной составляющей Нmx , т.е. структура волны Н10 начинает приближаться к структуре волны ТЕМ. Одновременно, как следует из (19), уменьшается разница между v^H10_ф и с. Аналогично можно интерпретировать и другие типы волн в прямоугольном волноводе.