Кольца, полукольца, мера на полукольце
Пусть задано некоторое непустое множество Х. Непустое семейство 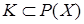 называется кольцом, если оно обладает тем свойством, что из А
называется кольцом, если оно обладает тем свойством, что из А  K и В
K и В  K следует А
K следует А 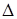 В
В  K, АÈВ
K, АÈВ  K.
K.
Утверждение 1. Пусть K 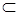 P(X) – кольцо. Тогда для любых А, В
P(X) – кольцо. Тогда для любых А, В  К выполнено АÇВ
К выполнено АÇВ  K и А\В
K и А\В  K.
K.
Таким образом, кольцо множеств есть система множеств, замкнутая по отношению к взятию суммы и пересечения, вычитанию и образованию симметрической разности. Любое кольцо содержит пустое множество Ø, так как всегда А\A=Ø. Система, состоящая только из пустого множества, представляет собой наименьшее возможное кольцо множеств.
Кольцо K называется алгеброй, если Х  K. Х в этом случае называется единицей кольца.
K. Х в этом случае называется единицей кольца.
Утверждение 2. Пусть непустая система K 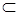 Р (Х) и K ¹Ø обладает свойствами:
Р (Х) и K ¹Ø обладает свойствами:
1) 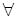 А
А  K
K 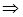 СА
СА  K;
K;
2) 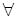 А, В
А, В  K
K 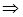 АÇВ
АÇВ  K.
K.
Тогда K является алгеброй.
Кольцо множеств называется s-кольцом, если оно вместе с каждой последовательностью множеств А1, А2,… содержит и их счетное объединение, т.е. 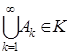 . s-алгеброй называется s-кольцо с единицей.
. s-алгеброй называется s-кольцо с единицей.
В теории меры часто приходится расширять произвольную систему множеств до кольца (алгебры) или s-кольца.
Теорема 1. Для любой непустой системы множеств S существует одно и только одно кольцо K(S), содержащее S и содержащееся в любом кольце K, содержащем S.
Непустая система S 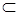 Р(Х) подмножеств множества Х называется полукольцом, если она содержит пустое множество, замкнута по отношению к образованию пересечений и обладает тем свойством, что если А, В
Р(Х) подмножеств множества Х называется полукольцом, если она содержит пустое множество, замкнута по отношению к образованию пересечений и обладает тем свойством, что если А, В  S, то найдется конечная система С1,…,Сn попарно непересекающихся множеств из S, что А\В=
S, то найдется конечная система С1,…,Сn попарно непересекающихся множеств из S, что А\В= 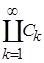 .
.
Отметим, что если S – полукольцо множеств, то для А, В  S элементы А\В и
S элементы А\В и 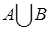 в общем случае не будут принадлежать S.
в общем случае не будут принадлежать S.
Теорема 2. Пусть S – полукольцо, тогда минимальное кольцо K(S), порожденное S, состоит из непересекающихся конечных объединений множеств из S, т.е. 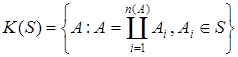 .
.
Пусть на некотором множестве Х задано полукольцо S 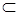 Р(Х). Будем говорить, что на S задана мера, если каждому элементу А
Р(Х). Будем говорить, что на S задана мера, если каждому элементу А  S поставлено в соответствие вещественное число m(A)
S поставлено в соответствие вещественное число m(A)  R таким образом, что выполнены следующие условия:
R таким образом, что выполнены следующие условия:
1) 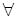 A
A  S : m(A)
S : m(A) 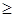 0;
0;
2) если 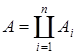 , A, Ai
, A, Ai  S, то
S, то 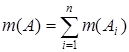 .
.
Таким образом, мера есть числовая функция множества S, но не является отображением из Х в R.
Дата добавления: 2021-07-22; просмотров: 683;











