Свойства меры на кольце
1) монотонность меры. Если А, В  K и А
K и А 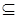 В, то m(A)
В, то m(A) 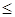 m(B);
m(B);
2) если А, В  К и А ÍВ, то m(B\A) = m(B)-m(A);
К и А ÍВ, то m(B\A) = m(B)-m(A);
3) если А, В  K, то m(AÇB) = m(A)+m(B)-m(AÈB);
K, то m(AÇB) = m(A)+m(B)-m(AÈB);
4) если А, В  K, то m(A
K, то m(A 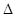 B) =m(A)+m(B)-2m(AÈB);
B) =m(A)+m(B)-2m(AÈB);
5) для любых множеств А, В  K выполняется |m(A)-m(B)|
K выполняется |m(A)-m(B)| 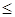 m(A
m(A 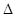 B);
B);
6) для любых множеств А, В, С  K имеет место следующее неравенство: m (A
K имеет место следующее неравенство: m (A 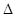 B)
B) 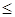 m(A
m(A 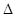 C)+m(C
C)+m(C 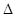 B).
B).
Мера m называется счетно-аддитивной (σ-аддитивной), если для любых А1, А2, …  S таких, что
S таких, что 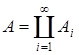 , A
, A  S выполнено
S выполнено 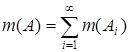 .
.
7) счетная полуаддитивность меры. Пусть А1, А2,…  K и
K и 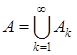 , А
, А  K и пусть мера m – σ-аддитивна, тогда
K и пусть мера m – σ-аддитивна, тогда 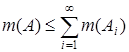 .
.
Теорема 3. Длина является σ-аддитивной мерой на полукольце S, состоящем из полуинтервалов вида [a;b[.
Меру m, заданную на кольце K, называют непрерывной сверху, если для любой возрастающей последовательности множеств А1 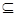 А2
А2 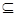 …
… 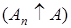 такой, что
такой, что 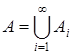 , где А, Аi
, где А, Аi  K справедливо равенство
K справедливо равенство 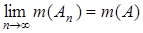 .
.
Меру m, заданную на кольце K, называют непрерывной снизу, если для любой убывающей последовательности множеств А1 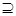 А2
А2 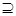 …
… 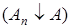 такой, что
такой, что 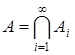 , А, Аi
, А, Аi  K справедливо равенство
K справедливо равенство 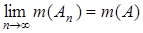 .
.
Если мера непрерывна сверху, то она непрерывна снизу и наоборот. Будем называть меру непрерывной, если она непрерывна сверху или снизу.
Теорема 4. Мера m, заданная на кольце K, является σ-аддитивной тогда и только тогда, когда она непрерывна.
Дата добавления: 2021-07-22; просмотров: 499;











