Пусть Z – множество целых чисел. Задает ли данная формула меру на Р (Z)
Задача 1. Пусть Z – множество целых чисел. Задает ли данная формула меру на Р (Z), если 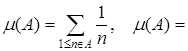 Ø, если А содержит только отрицательные числа.
Ø, если А содержит только отрицательные числа.
Решение. μ не является мерой, т.к. N 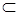 P(Z) и μ(N)=
P(Z) и μ(N)= 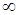 , т.е. μ не является отображением P(Z) в R.
, т.е. μ не является отображением P(Z) в R.
Задача 2. Пусть Х – произвольное множество. Выяснить, является ли мерой на Р(Х) cледующая функция множеств: μ(Ø)=0; 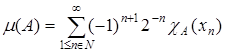 , где
, где 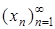 – фиксированная последовательность.
– фиксированная последовательность.
Решение. μ является отображением из P(X) в R, т.к. ряд 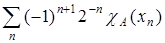 сходится, но не является мерой, потому что не выполнено условие положительности μ. Если множество А содержит только x2, то μ(А) = –0,25.
сходится, но не является мерой, потому что не выполнено условие положительности μ. Если множество А содержит только x2, то μ(А) = –0,25.
Задача 3. Пусть Х = [-1;1[, F : X 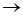 R и F(x)=sgn x, S – полукольцо, порожденное системой полуинтервалов {[a, b[, -1
R и F(x)=sgn x, S – полукольцо, порожденное системой полуинтервалов {[a, b[, -1 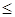 a < b <1}. Определим на S функцию μ по формуле μ ([a, b[) = F(b)-F(a). Является ли μ σ-аддитивной мерой.
a < b <1}. Определим на S функцию μ по формуле μ ([a, b[) = F(b)-F(a). Является ли μ σ-аддитивной мерой.
Решение. Функция F является неубывающей, ограниченной, имеющей одну точку разрыва х = 0. Следовательно, F порождает меру. Покажем, что мера μ не является σ-аддитивной. Рассмотрим полуинтервал [-1/2,0[ и представим его в виде счетного объединения попарно непересекающихся полуинтервалов:
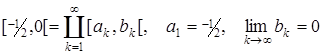 .
.
Тогда μ ( [-½, 0[ ) = F(0) –F(-½) = 0 – (–1) = 1.
Далее рассмотрим ряд
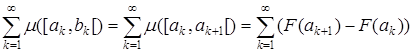 .
.
Составим последовательность частичных сумм этого ряда Sn=F(an) – F(a1) = (–1) – (–1) = 0. Следовательно, 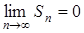 , но
, но 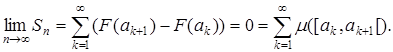
Итак, мы получили, что 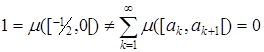 . Тем самым доказано, что мера μ не является σ-аддитивной. Обратим внимание, что функция F не является непрерывной слева.
. Тем самым доказано, что мера μ не является σ-аддитивной. Обратим внимание, что функция F не является непрерывной слева.
Задача 4. Пусть 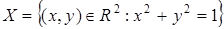 , S – совокупность дуг, содержащихся в X, замкнутых слева и открытых справа
, S – совокупность дуг, содержащихся в X, замкнутых слева и открытых справа 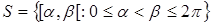 , h(x, y) – неотрицательная, непрерывная на прямоугольнике [0, 2π] ´ [0, 1] функция. Пусть
, h(x, y) – неотрицательная, непрерывная на прямоугольнике [0, 2π] ´ [0, 1] функция. Пусть 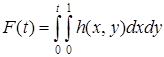 функция, заданная на [0,2π]. Положим
функция, заданная на [0,2π]. Положим
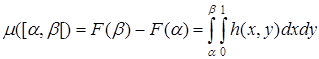 .
.
Задает ли F σ-аддитивную меру.
Решение. Функция F как интеграл Римана с переменным верхним пределом является неубывающей, непрерывной слева, следовательно, μ является σ-аддитивной мерой.
Задача 5. Пусть Х={a, b, c, d}, кольцо K=P(X). Определить на K меру так, чтобы μ({a})=10, μ({a, b})=100.
Решение. Для любого множества A  P(X) определим меру по формуле
P(X) определим меру по формуле 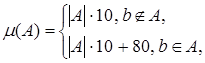
где 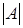 – количество элементов во множестве А. Простым перебором показывается, что μ – аддитивная функция.
– количество элементов во множестве А. Простым перебором показывается, что μ – аддитивная функция.
Задача 6. Пусть μ – мера, заданная на кольце множеств K. Доказать, что если для A, B  K и μ(А
K и μ(А 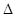 В) = 0, то μA = μB.
В) = 0, то μA = μB.
Доказательство. Воспользуемся свойством меры: 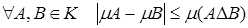 . Следовательно,
. Следовательно, 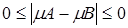 , т.е. μA = μB.
, т.е. μA = μB.
Задание 1. Образуют ли кольцо, σ-кольцо, алгебру, полукольцо следующие системы множеств:
1.1. Все ограниченные множества на прямой;
1.2. Все конечные множества на прямой;
1.3. Все счетные множества на прямой;
1.4. Все конечные множества натуральных чисел;
1.5. Все ограниченные замкнутые (компактные) множества на прямой;
1.6. Все всюду плотные множества в R;
1.7. Все множества, дополнения к которым конечны в R;
1.8. Все множества, дополнения к которым счетны в R;
1.9. Все компактные множества в R²;
1.10. Все выпуклые множества на плоскости;
1.11. Все множества, инвариантные относительно вращения вокруг начала координат;
1.12. Множество всех многоугольников на плоскости;
1.13. Все множества на плоскости, инвариантные относительно растяжений и сжатий;
1.14. Все конечные подмножества некоторого множества Х.
Задание 2. Пусть Х={a, b, c}, S = P(X). Построить, если возможно, меру на S так, чтобы:
2.1. m({a}) = 2, m({a, b}) = 5, m({a, b, c}) = 8;
2.2. m({b}) = 2, m({b, c}) = 6, m({a, b, c}) = 7;
2.3. m({c}) = 1, m({a, c}) = 5, m({c, b}) = 8;
2.4. m({a}) = 1, m({a, c}) = 4, m({a, b, c}) = 5;
2.5. m({b}) = 2, m({a, b}) = 3, m({a, b, c}) = 4;
2.6. m({c}) = 1, m({b, c}) = 4, m({a, c}) = 6;
2.7. m({a, b}) = 2, m({b, c}) = 4, m({a, c}) = 6;
2.8. m({a, c}) = 5, m({c, b}) = 6, m({a, b}) = 8;
2.9. m({c}) = 3, m({a, c}) = 5, m({b, c}) = 4;
2.10. m({b, c}) = 5, m({a, c}) = 5, m({a, b, c}) = 10;
2.11. m({a, b}) = 2, m({b, c}) = 6, m({a, b, c}) = 8;
2.12. m({b}) = 1, m({b, c}) = 2, m({a, b, c}) = 5;
2.13. m({a, c}) = 5, m({a, b}) = 7, m({a, b, c}) = 8;
2.14. m({c}) = 3, m({b, c}) = 4, m({a, c}) = 5.
Задание 3. Пусть Х=N. K – кольцо, состоящее из конечных подмножеств N. Задает ли данная формула меру на K?
3.1. 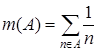 ; 3.2.
; 3.2. 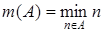 ;
;
3.3. 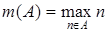 ; 3.4.
; 3.4. 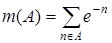 ;
;
3.5. 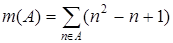 ; 3.6.
; 3.6. 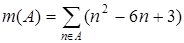 ;
;
3.7. 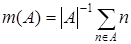 – среднее арифметическое;
– среднее арифметическое;
3.8. 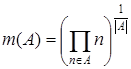 – среднее геометрическое;
– среднее геометрическое;
3.9. 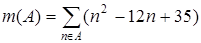 ; 3.10.
; 3.10. 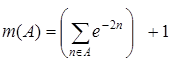 ;
;
3.11. 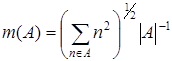 – среднее квадратическое;
– среднее квадратическое;
3.12. 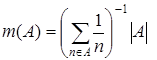 – среднее гармоническое;
– среднее гармоническое;
3.13. 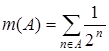 ; 3.14.
; 3.14. 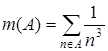 ,
,
где 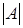 – количествово элементов множества А.
– количествово элементов множества А.
Задание 4. Пусть Х=[-1;1[, S = {[a,b[ 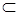 X}, m([a,b[) = F(b) –F(a). При каких значениях параметра a эта формула задает меру, σ-аддитивную меру. Если мера не является σ-аддитивной, то указать полуинтервал [a, b [ и его разбиение
X}, m([a,b[) = F(b) –F(a). При каких значениях параметра a эта формула задает меру, σ-аддитивную меру. Если мера не является σ-аддитивной, то указать полуинтервал [a, b [ и его разбиение 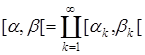 такое, что
такое, что 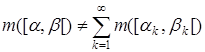 .
.
4.1. 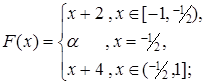 4.2.
4.2. 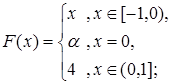
4.3. 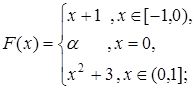 4.4.
4.4. 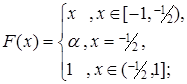
4.5. 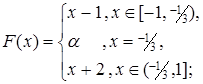 4.6.
4.6. 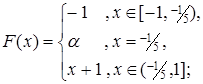
4.7. 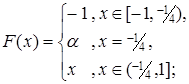 4.8.
4.8. 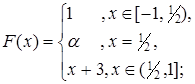
4.9. 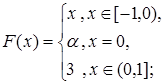 4.10.
4.10. 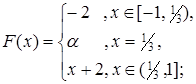
4.11. 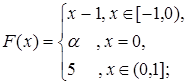 4.12.
4.12. 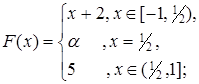
4.13. 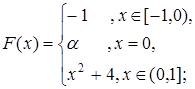 4.14.
4.14. 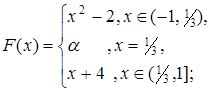
Дата добавления: 2021-07-22; просмотров: 559;











