Ориентирование линий
2.4.1. Азимуты и дирекционный угол, связь между ними
Ориентировать линию – значит определить ее направление относительно другой линии, принятой за исходную (начальную). Угол ориенти-рования (или направление) называется азимутом.
О.м. И.м. М.м.
    « «
 -g +d -g +d
a
С Рис. 2.9 |
И.м. – истинный меридиан
О.м. – осевой меридиан зоны (ось X)
М.м. – магнитный меридиан
g– сближение меридианов на плоскости
(восточное – положительное,
западное – отрицательное)
d – магнитное склонение
(восточное – положительное,
западное – отрицательное)
Азимуты отсчитываются от северной (положительной) части исходной линии по часовой стрелке. Азимут – величина положительная, изменяется от 0 до 360º.
В геодезии в качестве начальной линии обычно используют истинный меридиан, магнитный меридиан, ось Х. Углы ориентирования, отсчитываемые от этих линий, называются соответственно истинным азимутом А, магнитным азимутом Аm, дирекционным углом a .
Покажем в данной точке на карте (рис. 2.9) три меридиана.
Связь между углами ориентирования устанавливается формулами
a = A – g , Am = a + g – d .
Истинные азимуты используют при вычислении геодезических эллипсоидальных координат – широты и долготы. Истинный азимут можно измеритьс помощью гиротеодолита или астрономическими методами.
При ориентировании в закрытой местности используют магнитные азимуты. Магнитный азимут можно измерить с помощью буссоли (компаса).
На плоскости проекции используют дирекционные углы. Дирекционный угол измерить с достаточной точностью нельзя – его можно только вычислить.
2.4.2. Передача дирекционного угла на стороны геодезических сетей
Дирекционные углы вычисляют по исходному дирекционному углу и горизонтальным углам между линиями геодезических построений. Горизонтальные углы измеряют специальным прибором - теодолитом.
На рис. 2.10 показан теодолитный ход – геодезическая сеть, в которой измерены все линии и все углы между смежными линиями.
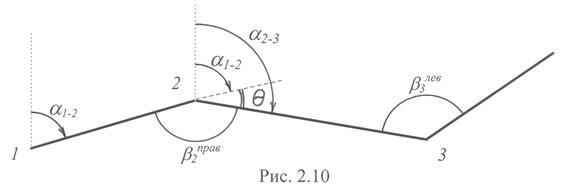
Пусть в этом ходе задан дирекционный угол линии 1–2 (a1-2). Тогда
a2-3 = a1-2 + q = a1-2 + 180° – b2прав .
Так как b прав = 360° – b лев, то a2-3 = a1-2 – 180° + b2лев .
Общая формула a2-3 = a1-2 ±180°±  . (2.1)
. (2.1)
Формула (2.1)передачи дирекционного угла – одна из основных формул геодезии. Угол q называется углом поворота.
2.5. Геодезические задачи на плоскости (преобразование координат)
При обработке результатов геодезических измерений постоянно преобразуюткоординаты: полярные в прямоугольные и обратно.
2.5.1. Прямая геодезическая задача
(преобразование полярных координат в прямоугольные)
Так в геодезии называется определение координат конечной точки линии по ее длине, направлению и координатам начальной точки (рис. 2.11).
Формулы прямой геодезической задачи используются наиболее часто при вычислении координат пунктов геодезических опорных сетей всех уровней точности. Длины линий измеряют, а дирекционные углы вычисляют по формуле (2.1) передачи дирекционного угла.
 X
Dy X
Dy
    x2 2
a x2 2
a
 Dx d Dx d
  x1
1 x1
1
 Y
y1 y2
Рис. 2.11 Y
y1 y2
Рис. 2.11
|
Дано: x1 , y1 ,a, d .
Найти: x2 , y2 .
Решение:
x2 = x1 + Dx ,
y2 = y1 + Dy ,
Dx = d×cosa ,
Dy = d×sina .
2.5.2. Обратная геодезическая задача
(преобразование прямоугольных координат в полярные)
Так в геодезии называется определение длины и направления линии по заданным координатам ее начальной и конечной точек (рис. 2.11).
Дано: x1 , y1 , x2 , y2 .
Найти: a, d .
Решение: 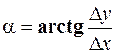 ;
; 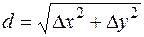 ;
;
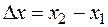 ;
; 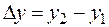 .
.
Формулы обратной геодезической задачи используют при вычислении геодезической привязки, при подготовке данных для выноса проекта сооружения в натуру и других работах.
2.5.3. Использование вычислительной техники при решении
геодезических задач
Практически любая геодезическая работа включает решение прямой и обратной геодезических задач. В прежние времена геодезические задачи решали с помощью таблиц тригонометрических функций, а значение угла ориентирования получали в пределах ±90°. Например,
Dx = –100 м, Dy = –100 м, r = arctg(Dy/Dx) = arctg1 = +45°.
Такой угол называют табличным, а в геодезии – румбом (r). Переход от румба к дирекционному углу выполняли по тригонометрическим формулам приведения. В указанном примере a = r + 180° = 225°. Об этом можно прочитать в любом учебнике. Однако понятие румба давно устарело, при использовании современной вычислительной техники румбы не вычисляют.
Решение всех геодезических задач выполняется в табличной форме. В пакете любого табличного процессора имеется константа pи специальная функция ATAN2 для решения обратной геодезической задачи. При использовании этой функции значение угла ориентирования получается в пределах ±p. Для перехода к дирекционному углу нужно ввести условия:
если Dy > 0 , тоa = a ,
в противном случаеa= a + 360° .
При решении обратной геодезической задачи с помощью пакета ЕXCEL в ячейку, где будет вычисляться дирекционный угол, нужно ввести формулу
если((e1–d1)>0;ATAN2((c1–b1);(e1–d1))*180/ПИ( );ATAN2((c1–b1);
(e1–d1))*180/ПИ( )+360)
Функция ATAN2 имеется на любом инженерном калькуляторе.
Все инженерные калькуляторы имеют специальные клавишидля решения обратной и прямой геодезических задач.Этоклавиши Þrθ или RÞP на однострочных калькуляторах и клавиша Pol( на двустрочных калькуляторах для преобразования прямоугольных координат R (rectangular) в полярные координаты Р (polar) и клавиши Þxy или PÞR на однострочных калькуляторах и Rec( на двустрочных калькуляторах для преобразования полярных координат в прямоугольные.
На многих однострочных калькуляторах имеются специальные клавиши двух дополнительных регистров памяти а и b, куда вносят исходные данные и где хранятся результаты. Такие калькуляторы позволяют получать окончательные результаты без всяких промежуточных записей.
На двустрочных калькуляторах типа Casio fx-82MS исходные данные вводят через запятую, обозначенную на специальной клавише, а результаты хранятся в регистрах памяти E и F.
На калькуляторах типа Citizen SR-281 исходные данные тоже вводят через запятую, а для вызова второго результата используют клавишу xÛ y.
На калькуляторах типа STF-169 исходные данные вводят через красную запятую, расположенную над клавишей 0, с предварительно нажатой клавишей ALFA.Результаты хранятся в регистре, обозначенном цифрой 0 – при решении обратной геодезической задачи – и в регистре, обозначенном .(десятичная точка) – при решении прямой геодезической задачи.
При решении обратной геодезической задачи калькулятор выдаёт дирекционные углы в пределах ±180º. Если ответ получается со знаком «–», то на однострочных калькуляторах к нему нужно просто прибавить 360º.
Примеры решения обратной геодезической задачи по данным:
1)Dx = –296,44 м,Dy = 120,50 м; 2) Dx = –333,04 м,Dy = –122,93 м
Калькулятор Citizen SR-135
296.44 ± a 120.50 b SHIFT a (длина линии) 319.9951931
b (дирекционный угол) 157.8787323
SHIFT DMS 157º 52′ 43,43″ = 157º 52,7′
333.04 ± a 122.93 ± b SHIFT a (длина линии) 355.0034176
b(дирекционный угол) –159.7401491
+ 360 =200.2598509 SHIFT DMS 200º 15′ 35,46″ = 200º 15,6′
Калькулятор STF-169
296.44 ± ALFA 0 120.50 Shift 0 (длина линии) 319.9951931
► (дирекционный угол) 157.8787323
SHIFT DMS 157º 52′ 43,43″ = 157º 52,7′
Калькулятор Citizen SR-281
2nd R®P 296.44 ± 2nd ,120.50 = (длина линии) 319.9951931
2nd xÛ y 2nd °¢ ² (дирекционный угол) 157° 52¢ 43²44
Двустрочный калькулятор Casio fx-82MS (а также -83, 85, 270, 300, 350MS)
Pol( –296.44 , 120.50) = (длина линии) 319.9951931
RCL tan-1 (дирекционный угол) 157.8787323 º′ ″ 157º52º43,4
(калькулятор и градусы, и минуты обозначает значком градусов).
Если дирекционный угол получается отрицательным, то на этом калькуляторе прибавить сразу 360º не удастся. Нужно результат переписать в другой регистр памяти (например, А), а затем вызвать его оттуда и прибавить 360:
Pol(–333.04 , –122.93) = (длина линии) 355.0034176
RCL tan-1 –159.7401491
SHIFT STO A (запись в регистр А)
ALFA A (вызов из регистра А) + 360 = 200.2598509
º′ ″ 200º 15º 35,4 = 200º 15,6′
При решении прямой геодезической задачи калькулятор воспринимает дирекционные углы от 0 до 360º.
Примеры решения прямой геодезической задачи по данным:
1) d = 204,42 м, α = 262°40′00″; 2) d = 226,09 м, α = 343°02′42″
Калькулятор Citizen SR-135
204.42 а 262.4000 DMS b SHIFT b (Δx) – 26.09 b (Δy) –202.75
226.09 а 343.0242 DMS b SHIFT b (Δx) +216.26 b (Δy) – 65.93
Калькулятор STF-169
204.42 ALFA 0 262.4000 DMS SHIFT .(Δx) –26.09 ► (Δy) –202.75
226.09 ALFA 0 343.0242 DMS SHIFT . (Δx) +216.26 ► (Δy) – 65.93
Калькулятор Citizen SR-281
2nd P®R 204.42 2nd ,262 º′ ″ 40.0 º′ ″ = (Δx) –26.09
2nd xÛ y (Δy) –202.75
Калькулятор Casio fx-82MS
SHIFT Pol(204.42 , 262 º′ ″ 40.0 º′ ″) = –26.09 RCL tan-1 –202.75
SHIFT Pol(226.09 , 343 º′ ″02.7 º′ ″) = 216.26 RCL tan-1 – 65.93
2.6. Изображение рельефа на топографических картах и планах
2.6.1. Основные определения
Рельеф – это совокупность неровностей земной поверхности. Современный рельеф сложился в результате горообразования и действия текучих вод. Рельеф и гидрография составляют основное содержание топографической карты с точки зрения инженера-путейца, так как именно эти два элемента местности определяют стоимость строительства и содержания железной дороги. Основная задача при трассировании железной дороги – выбор попутных благоприятных форм рельефа.
На топографических картах и планах рельеф изображается совокупностью условных знаков: горизонталями, бергштрихами, отметками точек и специальными условными знаками для показа крутых склонов. Для изображения рельефа используют коричневый цвет.
Горизонталь– линия, соединяющая точки с одинаковыми высотами. Горизонтали – плавные, замкнутые, непересекающиеся линии, получающиеся как след от сечения местности уровенными поверхностями, проведенными через равные интервалы. Этот интервал, т.е. расстояние ho между смежными уровенными поверхностями, считаемое по отвесной линии, называется высотой сечения рельефа(или сечением рельефа). Высота сечения зависит от характера местности, масштаба, назначения карты и в среднем определяется по формуле ho = 0,2×M , где М – знаменатель масштаба. Высота сечения подписывается на каждом листе топографической карты (плана) ниже масштаба. На планах применяют высоты сечения рельефа 0.5 м, 1 м, 2 м и 5 м; на топографических картах 2.5 м, 5 м, 10 м, 20 м и 40 м.
Виды горизонталей:
– основные; их проводят через превышения, равные высоте сечения;
– основные утолщенные; их применяют для облегчения счета горизонталей и большей наглядности рисунка рельефа; утолщается каждая пятая горизонталь при высоте сечения 1; 2; 5; 10; 20 м и каждая четвертая или десятая при высоте сечения 0.5 и 2.5 м;
– дополнительные (полугоризонтали); их проводят через половину высоты сечения;
– вспомогательные; их проводят на произвольной высоте.
Дополнительные и вспомогательные горизонтали показывают пунктиром. Толщина основных, дополнительных и вспомогательных горизонталей на планах принята равной 0.15 мм, утолщенных – 0.25 мм.
На картах и планах надписывают отметки точек местности, горизонтали (в их разрыве), относительные высоты отдельных форм рельефа. Надписи горизонталей ориентируют основанием цифр вниз по скату. Надписываться может любая горизонталь. Обычно надписывают утолщенные горизонтали.
Направление ската показывают с помощью бергштрихов(длиной 0.5 мм), которые ставят в характерных местах рельефа перпендикулярно горизонталям и ориентируют по скату.
На каждом квадратном дециметре плана подписывают не менее 5 отметок с включением наиболее характерных точек данной территории.
Расстояние между смежными горизонталями в плане называется заложением do. Угол наклона ската v называется крутизной ската. Очевидно, чем круче скат, тем меньше заложение. Связь между элементами ската устанавливается по рис. 2.12.
Уклончисленно равен тангенсу угла наклона ската:
i = tgv = ho/do .
Железнодорожники уклон выражают в тысячных долях единицы – промилле (‰ ). Например, ho = 1 м, do = 100 м, i = 0.010 = 10‰ .
По топографическим картам можно определять уклоны и крутизну ската, проводить линии с заданным уклоном, строить профили по заданным направлениям, определять водосборные площади и т.д.
2.6.2. Основные формы рельефа, их изображение горизонталями
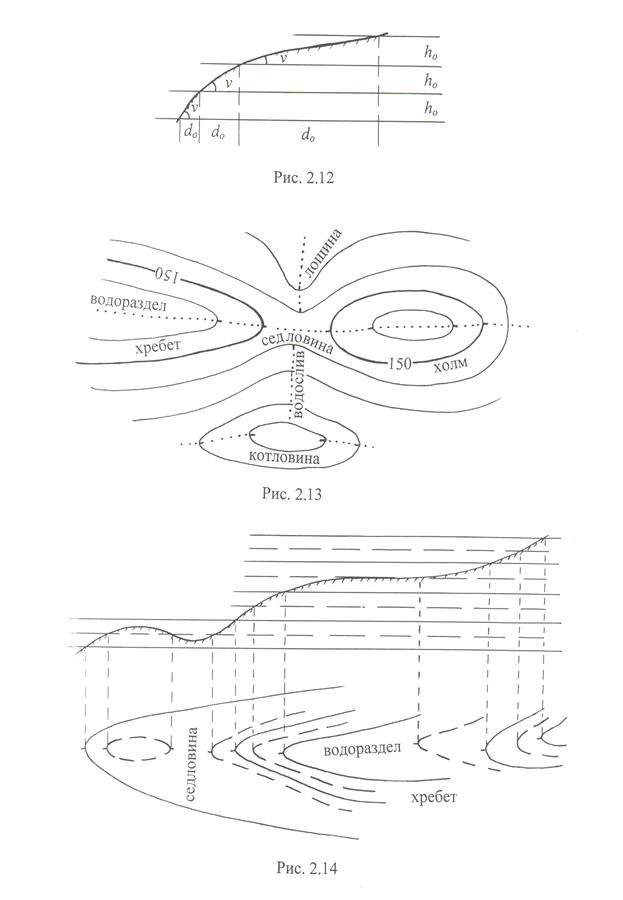
Всё многообразие форм рельефа можно свести к четырём основным и пятой производной: холм, котловина, хребет, лощина, седловина (рис. 2.13).
Холм – замкнутая выпуклая форма рельефа.
Котловина – замкнутая вогнутая формарельефа.
Хребет – вытянутая в одном направлении возвышенность.
Лощина – вытянутое в одном направлении понижение.
Пятая форма рельефа – седловина –это понижение между двумя возвышенностями, где сходятся два хребта и две лощины. Рисунок седловины обязательно включает четыре горизонтали. Бергштрихи на горизонталях хребтов направлены навстречу друг другу, на горизонталях лощин – в противоположные стороны.
Линия пересечения склонов хребта называется водоразделом. Линия пересечения склонов лощины называется водосливом (тальвегом). Водораздел и водослив – это две основные (структурные) линии рельефа.
Следует помнить, что линии водораздела и водослива проходят по местам наибольшего изгиба горизонталей и что на изображениях хребтов горизонтали имеют изгиб от вершины, а на изображениях лощин – к вершине.
Определять направление ската, проводить водораздельные и водосливные линии – основные задачи при чтении рельефа на карте.
Для показа характерных деталей рельефа, не изображающихся основ-ными горизонталями, а также изменений в крутизне склонов, используют дополнительные горизонтали (рис. 2.14). Дополнительные горизонтали обязательно проводят на участках, где расстояния между основными горизонталями превышает 2,5 см на плане.
Средние погрешности положения горизонталей не должны превышать 1/4 высоты сечения при углах наклона до 2 градусов и 1/3 при углах наклона от 2 до 6 градусов.
2.6.3. Цифровые модели местности и рельефа
Топографические карты и планы могут быть представлены в графическом и цифровом виде. Графическая (бумажная) карта более привычна. На такой карте информация о местности представлена в образно-знаковой форме. Цифровая карта, или цифровая модель местности (ЦММ) – это запись картографической информации о местности в цифровом виде на машинных носителях. ЦММ представляет собой отображение в виде пространственных координат множества точек земной поверхности, объединённых в единую систему по определённым математическим законам. Цифровая карта по содержанию полностью аналогична графической карте. Точность ЦММ отвечает точности топографических карт и планов соответствующих масштабов.
Цифровая карта (ЦММ) может быть выведена на экран монитора в виде электронной карты. ЦММ позволяют автоматизировать составление топографических карт и планов в разных масштабах, их обновление, тиражирование, выполнение проектирования и инженерных расчётов. Для этой цели разработано много программных комплексов (Кредо и др.).
Частью цифровой модели местности является цифровая модель рельефа (ЦМР). При съёмке местности точки выбирают на перегибах структурных линий рельефа и в местах изменения крутизны склонов. Получаемая таким образом ЦМР называется структурной.
По ЦМР можно провести горизонтали, т.е. преобразовать цифровую форму изображения рельефа в аналоговую. При проведении горизонталей по ЦМР с помощью ЭВМ точки с известными отметками по специальным программам располагаются в вершинах треугольников.
С помощью специальных устройств (сканеров, дигитайзеров) возможно обратное преобразование – аналоговой формы изображения рельефа в цифровую.
Цифровые модели местности и рельефа служат основой для составления геоинформационных систем (ГИС) – см. гл. 12.
Дата добавления: 2017-06-13; просмотров: 2825;

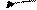
 Аm
Аm
 А
А В
В









