ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ ЛИНИЙ
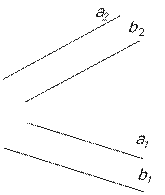
Если две прямые в пространстве параллельны, то и параллельны между собой одноименные проекции прямых. Если а║b, то а1║b1, а2║b2.
Для того, чтобы судить о параллельности двух прямых общего положения в пространстве, необходима и достаточна параллельность их проекций на двух плоскостях проекций (рис.14).
Параллельность профильных прямых не может быть определена по фронтальным и горизонтальным проекциям этой прямой. Для оценки их взаимного положения необходимо обратиться к профильной проекции, по которой и делают окончательный вывод (рис.15).
Если [АВ]║[СD], то [А3В3]║[С3D3].
| 
|
| Рис.14 | Рис.15. |
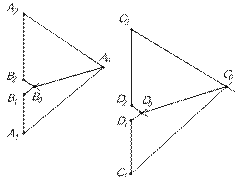
При безосной системе нужно сделать следующие построения (рис.16.). Применяя косоугольное проецирование строим А0В0 и С0D0.
|
| Рис. 16 |
[А1А0] ║ [В1В0] ║ [D1D0] ║ [С1С0] и
[А2А0] ║ [В2В0] ║ [D2D0] ║ [С2С0].
Если [В0А0]║ [D0С0], то │АВ│ ║ │СD│
Пересекающиеся прямые.
Пересекающиеся прямые имеют общую точку. Эта общая точка должна быть как в пространстве, так и на эпюре (рис.17).
Если прямые пересекаются, то точки пересечения их одноименных проекций должны находиться на одной линии связи. a  b=K; a1
b=K; a1  b1=K1; a2
b1=K1; a2 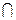 b2=K2.
b2=K2.
Для заключения о пересечении прямых общего положения достаточно иметь их проекции на две плоскости проекций.
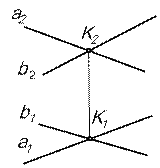
Если пересекаются профильные прямые, то необходимо построить их профильные проекции, а при безосной системе сделать дополнительные построения (рис.18).
| 
|
| Рис.17 | Рис.18. |
| Если [А0В0] ∩ [D0С0]=К0, то [АВ] ∩ [DC]=К. [А1А0] ║ [С1С0] ║ [В1В0] ║ [К1К0] и [А2А0] ║ [С2С0] ║ [В2В0] ║ [К2К0]. |
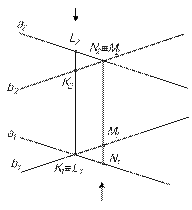
Скрещивающиеся прямые.
|
| Рис.19 |
Если прямые не пересекаются и не параллельны между собой, то точки пересечения их одноименных проекций не лежат на одной линии проекционной связи (рис.19).
L и К – на одном перпендикуляре к 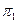 .
.
М и N – на одном перпендикуляре к 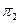 .
.
Дата добавления: 2017-10-04; просмотров: 1520;











