Деформационная теория при одноосном растяжении

При одноосном нагружении тензоры напряжений и деформаций имеют вид:

, ,

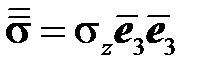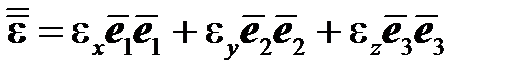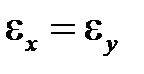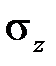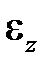где деформации, характеризующие сужение материала в направлениях, поперечных направлению нагружения, в силу изотропии материала равны друг другу . Такой вид нагружения удобен для наглядного представления закономерностей деформирования и нагружения, поскольку тензоры напряжений и деформаций при этом отображаются скалярами и (рис.1.1).

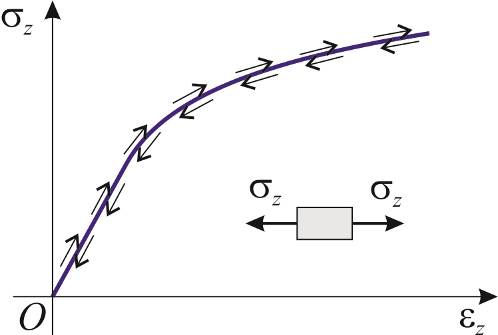
Рис.1.1

За недеформированное состояние примем ненагруженное, поэтому если 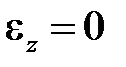, то и 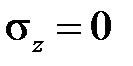. Заметим, что устойчивость упругого материала требует, чтобы функция 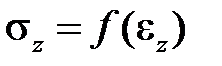, изображенная на рис.1.1, была монотонно возрастающей, поэтому существует и обратная функция , также монотонная. Модель материала, согласно которой точка состояния ( 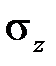, 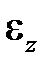) в процессе нагружения и разгрузки скользит по одной и той же кривой

,

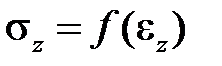называется теорией малых упругопластических деформаций, или деформационной теорией. Добавим, что эта теория также представляет собой модель нелинейно упругого материала с диаграммой, снимаемой с образца при нагружении, без проверки того, как выглядит процесс разгрузки.

При неизотермическом нагружении упругого тела деформация однозначно зависит от напряжения и температуры T

.

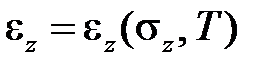Вспомним, что деформацию при нулевом напряжении называют тепловой 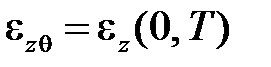. Температура, при которой 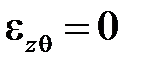, считается началом отсчета T₀ . Зависимость деформаций от напряжений удобнее записывать в виде суммы

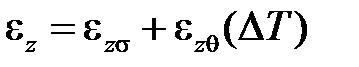, DT = T – T₀, (1.1)

разделяя деформацию на слагаемые: силовую деформацию 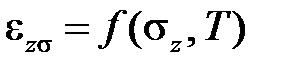и тепловую 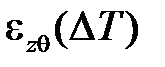. При снятии напряжения силовая деформация упругого материала исчезает. Выражение (1.1) определяет линейно или нелинейно ведет себя упругое тело в случае неизотермического нагружения. Линейно упругое тело определяется выражением

.

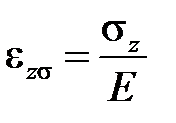Свойство упругости позволяет экспериментально определять тепловую деформацию 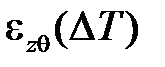, нагревая ненагруженные образцы. Зависимость тепловой деформации от температуры близка к линейной

,

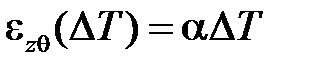где a – это коэффициент теплового расширения. Иногда это выражение уточняют следующим образом

,

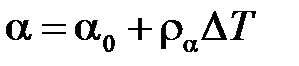где a₀ иr_a – это константы материала: величина a₀представляет значение производной 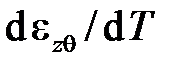при температуре начала отсчета T₀. Заметим, что в справочниках часто задают среднее значение a в том или ином температурном диапазоне, с тем или иным началом отсчета. Зависимость напряжений от деформаций имеет вид

,

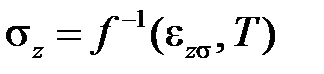где 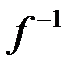– это функция, обратная функции f по первому аргументу.