Деформационная теория при сложном нагружении

Из постулата симметрии следует, что при простом нагружении происходит и простое деформирование с тем же направляющим девиатором

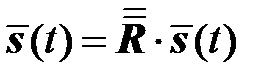
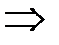
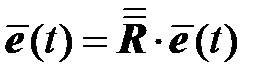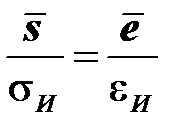, . (2.1)

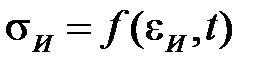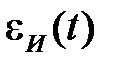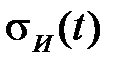Поскольку любые траектории любых двух простых нагружений всегда подобны, то и траектории соответствующих деформаций в L₅ также подобны. Следовательно, зависимости при всех простых нагружениях (растяжение, сжатие, сдвиг, растяжение со сдвигом) с одинаковой историей или одинаковы. Эти соображения с учетом ряда других лежат в основе деформационной теории.

Для склерономного материала с оговоркой на монотонность нагружения, можно утверждать, что при простом нагружении зависимость 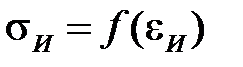одинакова и не зависит от направления направляющего девиатора. Если снять требование простоты нагружения и, таким образом, исключить из выражения (2.1) требование постоянства направляющих девиаторов, то получим деформационную теорию (теорию малых упругопластических деформаций), включающей в себя три основных соотношения:

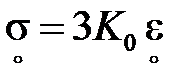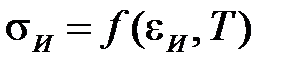, , . (2.2)

Здесь в первом соотношении 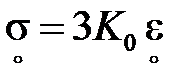постулируется линейная связь шаровых частей тензоров напряжений и деформаций, что подтверждается экспериментами. В третьем соотношении 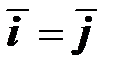постулируется равенство направляющих девиаторов, наблюдаемое в изотропных средах, строго говоря, лишь при простых нагружениях. Второе соотношение 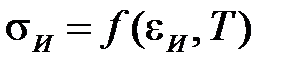является основным допущением, превращающим деформационную теорию в теорию нелинейной упругости, согласно которой свойства изотропных неупругих материалов, которые обнаруживаются при монотонном простом нагружении, абсолютизируются и предполагаются справедливыми при всех обстоятельствах. Все это позволяет получить весьма простую модель, сыгравшую, поэтому, важную роль в реологии.

Функцию, выражающую связь интенсивностей напряжений и деформаций при заданной температуре T

,

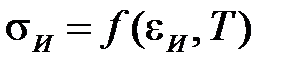называют обобщенной диаграммой деформирования (единой кривой деформирования в интенсивностях). Для ее построения можно использовать аппроксимацию (2.9), где модуль упрочнения m₀ определяют из выражения (2.7). При пропорциональном нагружении изотропных материалов такая аппроксимация хорошо подтверждается экспериментами. Для удобства также можно использовать более простую зависимость (2.1).

Девиатор деформации представляет собой сумму двух слагаемых: упругого 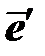и неупругого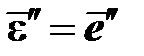

.

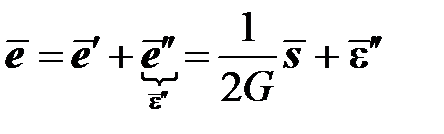С учетом этого выражения, а также принципа симметрии, следующего из постулата изотропии Ильюшина, траектория деформаций в девиаторном пространстве L₅ подобна не только траектории напряжений, но и траектории ее неупругой составляющей

,

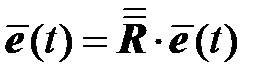
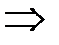
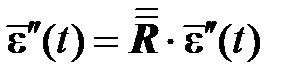что означает равенство направляющих девиаторов

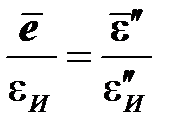
и обусловливает связь соответствующих интенсивностей (рис.2.3б)

.

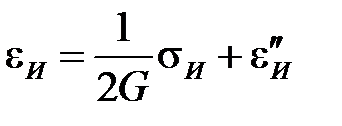Требование устойчивости материала в деформационной теории сводится к ограничениям на значения упругих характеристик, наследуемым из теории упругости, и к требованию положительности производной функции 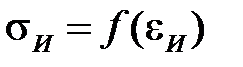. Иногда диаграмма деформирования принимается в виде диаграммы идеально пластического материала (например, при одноосном растяжении участок упругого деформирования 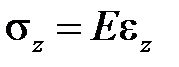сменяется участком предельного состояния 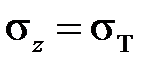, на котором производная равна нулю). Это предельный случай границы между устойчивым и неустойчивым материалом, при котором возможно лишь кинематическое нагружение.

При деформировании пластичных материалов пластические деформации, как правило, существенно больше упругих, поэтому принимается, что при пластическом деформировании изменение объема пренебрежительно мало. На основании этого по­ложения вводится гипотеза о несжимаемости материала.