Глава 3. ОРИЕНТИРОВАНИЕ ЛИНИЙ
3.1. Ориентирование. Ориентирующие углы
Ориентировать линию местности - значит определить ее направление. Под направлением линии понимают горизонтальный угол, образованный данной линией и другой, положение которой известно. Линии, положение которых известно или может быть весьма точно определено в любой точке земной поверхности, - меридианы: истинные или географические и магнитные. Горизонтальные углы, определяющие направления линий местности, называются ориентирующими. Это: истинные (географические) и магнитные азимуты и румбы; дирекционные углы и румбы.
3.2. Истинные азимуты и румбы линий местности
Истинным азимутом линии местности в данной точке называется горизонтальный угол А (рис. 2.17), отсчитываемый по ходу часовой стрелки от северной части истинного (географического) меридиана этой точки до ориентируемой линии. Истинные азимуты принимают значения от 0 до 360˚. В геодезии принято различать прямое и обратное направления линий местности. Так, если KL считать прямым направлением линии, то LK будет обратным направлением той же линии. В соответствии с этим угол А является прямым азимутом линии KL в точке M, а угол А' - обратным. Из рис. 17 видно, что 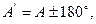 (3.1)
(3.1)
т.е. прямой и обратный азимуты линии в данной точке разнятся на 180˚ . В разных точках Земли меридианы не параллельны между собой, поэтому азимуты одной и той же линии в различных ее точках будут неодинаковы. Так, в точках Мо и М1 линии KL (см. рис. 3.1) истинные меридианы СоЮо и С1Ю1 не параллельны меридиану СЮ точки М. Поэтому азимуты линии KL в точках Мо и М1 равны
- 21-
соответственно Ао и А1. Если провести в этих точках линии С'Ю'΄, параллельные меридиану СЮ точки М, то 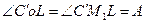 . Поэтому
. Поэтому
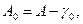 (3.2)
(3.2)
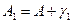 (3.3)
(3.3)
где 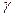 - сближение меридианов - угол между меридианами различных точек местности. Условились, для точек, расположенных к востоку (в точке М1 ) от данной точки (М), считать сближение положительным, а для точек, расположенных к западу от данной точки (в точке Мо), - отрицательным. Азимут линии KL в точке М1 согласно (3.1) будет
- сближение меридианов - угол между меридианами различных точек местности. Условились, для точек, расположенных к востоку (в точке М1 ) от данной точки (М), считать сближение положительным, а для точек, расположенных к западу от данной точки (в точке Мо), - отрицательным. Азимут линии KL в точке М1 согласно (3.1) будет  .
.
Подставив в эту формулу значение А по (3.2), получим
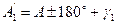 . (3.4)
. (3.4)
Истинные азимуты определяются из астрономических наблюдений.
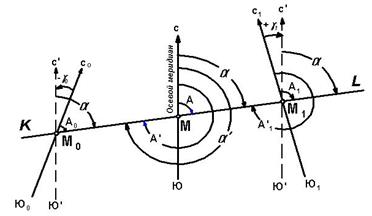
Рис. 3.1. Истинный азимут линии местности
Во многих случаях при ориентировании линий местности вместо азимутов пользуются румбами.
Истинным румбомлинии местности называется острый горизонтальный угол между ближайшей (северной или южной) частью истинного меридиана в данной точке и этой линией.
- 22 -
Численное значение румба сопровождают названием четверти, в которой находится линия.
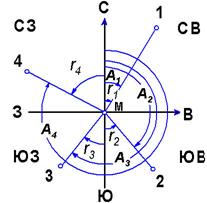 На рис. 3.2 показаны истинные
На рис. 3.2 показаны истинные
румбы линий во всех четырех
четвертях. Так, линия M-3 имеет
румб 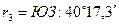 ;
;
линия M-4 имеет румб
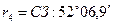 .
.
Из этого же рисунка видно, что
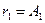 , (3.4)
, (3.4)
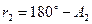 , (3.5)
, (3.5)
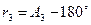 , (3.6)
, (3.6)
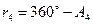 . (3.7)
. (3.7)
Эти формулы позволяют осу-
ществлять переход от азиму-
тов к румбам и обратно. Рис. 3.2. Связь азимутов ирумбов
3.3. Магнитные азимуты и румбы линий местности
Известно, что под влиянием земного магнетизма свободно подвешенная магнитная стрелка устанавливается в плоскости
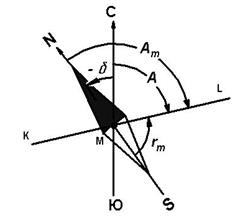
Рис. 3.3. Магнитные азимуты и румбы
- 23 -
магнитного меридиана данной точки. Это свойство магнитной стрелки позволяет ориентировать относительно нее линии местности.
Магнитным меридианом называется сечение поверхности Земли отвесной плоскостью, проходящей через концы магнитной стрелки, свободно подвешенной в данной точке.
Магнитным азимутом линии местности называется горизонтальный угол, отсчитываемый от северной части магнитного меридиана по ходу часовой стрелки до данной линии. Этот угол принимает значения от 0 до 360˚. Магнитным румбом линии местности называется острый горизонтальный угол, отсчитываемый от ближайшей части (северной или южной) магнитного меридиана до данной линии. На рис. 3.3: NS - магнитный меридиан, Аm – магнитный азимут линии KL в точке М, rm - магнитный румб этой линии, СЮ - истинный меридиан точки М, А - истинный азимут линии KL в точке М.
В каждой данной точке магнитный и истинный меридианы образуют между собой угол δ, называемый склонением магнитной стрелки. Северный конец магнитной стрелки может отклоняться от истинного меридиана к востоку или западу. В зависимости от этого различают восточное и западное склонение. Восточное склонение принято считать положительным, западное - отрицательным. Из рис. 3.3 видно, что
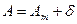 . (3.8)
. (3.8)
В различных точках Земли склонение магнитной стрелки имеет разную величину, так в пределах территории СНГ величина его колеблется от 0 до ±15˚. Но и в одной и той же точке она постепенно меняется. Различают суточные, годовые и вековые изменения склонений. Вследствие этого ориентирование линий с помощью магнитной стрелки допускается при топографо-геодезических работах, не требующих высокой точности. Форма записи магнитного румба соответствует форме записи истинного румба, включая формулы связи с азимутами.
3.4. Дирекционные углы и румбы линий местности
То обстоятельство, что азимуты линии в разных ее точках неодинаковы, ограничивает их использование для ориентирования геодезических построений, поэтому в большинстве случаев практики для этой цели используют дирекционные углы.
- 24 -
Дирекционным углом линии местности называется горизонтальный угол α, отсчитываемый по ходу часовой стрелки от северной части осевого меридиана зоны или линий ему параллельных до данной линии. Пусть СЮ (см. рис. 3.1) - осевой меридиан зоны, а С'Ю' - линии, ему параллельные; дирекционный угол линии KL в любой ее точке (Mо,M ,M1 и др.) равен α. Следовательно, в отличие от азимута дирекционный угол линии в любой ее точке сохраняет свою величину. Из рис. 3.1 видно, что прямой и обратный дирекционные углы линии разнятся между собой на 180˚, т.е.
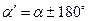 . (3.9)
. (3.9)
Понятие дирекционного румба rm, форма записи, cвязь с дирекционным углом - полностью соответствуют истинному и магнитному румбам. Для перехода от дирекционного угла α к дирекционному румбу r и обратно применяют формулы связи истинных азимутов Aи румбов. В связи с тем, что дирекционный румб используется широко и часто, слово «дирекционный» в его названии обычно опускают. Зависимость дирекционных углов с истинными и магнитными азимутами видна на рис. 3.1, 3.3 и выражается формулами:
 , (3.10)
, (3.10)
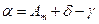 (3.11)
(3.11)
Средние величины 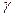 и
и 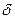 для территории, изображенной на листе топографической карты, приводятся за южной рамкой в виде текста и специальной диаграммы, показывающей взаимное расположение истинного, магнитного и осевого меридианов.
для территории, изображенной на листе топографической карты, приводятся за южной рамкой в виде текста и специальной диаграммы, показывающей взаимное расположение истинного, магнитного и осевого меридианов.
Приближенно сближение меридианов можно определить из следующих рассуждений. Примем в качестве фигуры относимости шар, равновеликий по объему эллипсоиду Ф.Н. Красовского, с радиусом 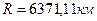 (рис. 3.4).
(рис. 3.4).
На параллели с широтой φвозьмем две точки К и L, линейное расстояние между которыми равно l км. В точках K и L проведем касательные к меридианам этих точек. Эти касательные называются полуденными линиями. Тогда угол γ между касательными представит сближение меридианов точек K и L. Для точек K и L, расположенных в пределах одной зоны, угол γ настолько мал, что расстоянии l можно рассматривать как дугу радиуса KT.
- 25 -
Тогда угол γ, выраженный в радианах, будет
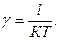 (3.12)
(3.12)
Но
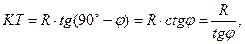
следовательно,
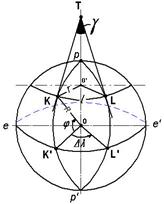
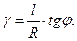 (3.13)
(3.13)
Так как в одном радиане 3438', то сближение меридианов, выраженное в минутах, будет равно
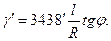 (3.14)
(3.14)
Подставив сюда вместо R его значение, получим
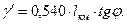 (3.15)
(3.15)
Если 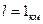 , то
, то
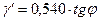 , (3.16)
, (3.16)
Рис. 3.4.Сближение меридианов
т.е. приближенно сближение меридианов на 1 км (выраженное в минутах) равно половине тангенса широты места.
При определении направлений во многих случаях погрешность в 1'считается допустимой. В таких случаях сближением меридианов на 1 км можно пренебречь, и на этом расстоянии меридианы в соответствующих точках можно рассматривать как параллельные.
3.5. Прямая и обратная геодезические задачи на плоскости
Прямая геодезическая задача. В геодезии и маркшейдерском деле часто приходится передавать координаты с одного пункта на другой. Зная исходные координаты XA, YA одного из концов отрезка линии местности AB, длину горизонтального проложения d и дирек-
- 26 -
ционный угол α, азимут A или румб r этой линии можно определить координаты XB, YBдругого конца отрезка ( рис. 3.5).
В такой постановке передача координат называется прямой геодезической задачей. Эта задача представляет значительные трудности при решении её для пунктов, расположенных на эллипсоиде; для пунктов на плоскости она решается следующим образом.
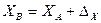 ;
; 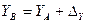 , (3.17)
, (3.17)
где 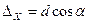 ;
; 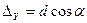 . (3.18)
. (3.18)
- приращения координат по осям абсцисс и ординат соответственно.

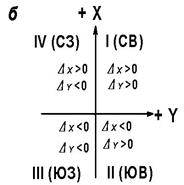
Рис. 3.5. Схемы к решению геодезических задач
Обратная геодезическая задача состоит в том, чтобы по известным координатам XA, YA, XB, YBконцов отрезка линии местности AB (см. рис. 3.5) определить длину горизонтального проложения d и направление α этой линии. Если, например, надо проложить по линии АВ просеку через лес или тоннель под проливом, то, рассчитав длину и направление линии, можно уверенно и с необходимой точностью выполнить поставленные задачи. Решение задачи выполняют в такой последовательности.
- 27 -
Вычисляют приращения координат 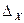 и
и 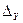 по формулам
по формулам
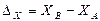 , (3.19)
, (3.19)
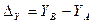 . (3.20)
. (3.20)
Находят численное значение румба rAB отрезка AB линии местности
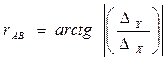 (3.21)
(3.21)
По знакам приращений координат (см. табл. 3.1) определяют название четверти, в которой расположен отрезок линии. От румба переходят к значению дирекционного угла α.
Для контроля правильности вычисленного румба можно воспользо-ваться формулой
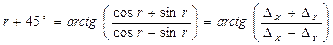 (3.22)
(3.22)
Полученный по этой формуле румб должен отличаться от вычисленного по формуле (3.21) ровно на 45˚ .
Таблица 3.1
Связь румбов и дирекционных углов
| Номер четверти | Название четверти | Знаки приращений координат | Значения дирекционных углов | |
| ∆Y | ∆X | |||
| I | СВ | + | + | 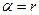
|
| II | ЮВ | + | - | 
|
| III | ЮЗ | - | - | 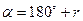
|
| IV | СЗ | - | + | 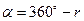
|
Длину горизонтального проложения d линии AB можно получить из прямоугольного треугольника (см. рис. 3.5).
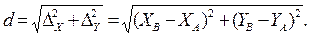 (3.23)
(3.23)
Для контроля dвычисляют по формулам
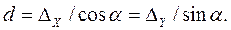 (3.24)
(3.24)
- 28 -
Дата добавления: 2021-07-22; просмотров: 607;











