ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ
4.1. Общие сведения об измерениях
Объектом изучения науки Геодезия является планета Земля – ее форма, размеры, внешнее гравитационное поле. Эти характеристики получают из различных измерений, выполняемых на поверхности Земли. Под измерением физической величины X понимают процесс сравнения этой величины с другой, однородной с ней величиной q, принятой в качестве меры - единицы измерения. Например, длину отрезка линии местности сравнивают с единицей линейных измерений - метром; горизонтальный угол, образованный отрезками линий на местности, сравнивают с градусом, градом, радианом.
Измерения различают: прямые; косвенные; равноточные; неравно-точные.
Под прямыми измерениями понимают такие, при которых определяемую величину получают путём непосредственного сравнения (сопоставления) её с единицей измерения или её производной. Например, длина отрезка линии измеряется стальной лентой или горизонтальный угол на местности измеряется теодолитом, а на бумаге транспортиром и т.д.
Косвенными называют измерения, определяемая величина в которых является функцией других непосредственно измеренных
величин. Так, для определения длины окружности или площади круга, необходимо непосредственно измерить радиус окружности.
Равноточными называют измерения, выполненные приборами одного класса точности, специалистами равной квалификации, по одной и той же технологии, в идентичных внешних условиях. При несоблюдении хотя бы одного из перечисленных условий измерения считаются неравноточными.
Результатом измерения l является число, показывающее, во сколько раз определяемая величина больше или меньше величины, с которой её сравнивали, т.е. величины, принятой за единицу измерения. Результаты измерений подразделяют на необходимые и добавочные (или избыточные). Так, если одна и та же величина (длина линии, угол треугольника и т.п.) измерена n раз, то один из результатов измерений является необходимым, а 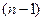 - добавочными. Добавочные измерения имеют весьма важное значение: их сходимость является средством контроля и позволяет судить о качестве результатов измерений; они дают возможность получить наиболее надежное значение искомой величины по сравнению с любым отдельно взятым результатом измерения.
- добавочными. Добавочные измерения имеют весьма важное значение: их сходимость является средством контроля и позволяет судить о качестве результатов измерений; они дают возможность получить наиболее надежное значение искомой величины по сравнению с любым отдельно взятым результатом измерения.
- 29 -
4.2. Погрешности результатов измерений
Результаты многократных измерений одной и той же физической величины (линии, угла, превышения и т.п.), как правило, различаются между собой и не совпадают с точным (истинным) значением измеряемой величины, т.е. содержат неизбежные погрешности, вызываемые различными причинами.
Под погрешностью 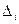 результата измерения
результата измерения 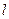 понимают разность между результатом измерения
понимают разность между результатом измерения 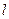 физической величины и точным (истинным) значением
физической величины и точным (истинным) значением 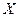 этой величины, т.е.
этой величины, т.е.
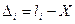 (4.1)
(4.1)
где 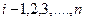 ; n - число выполненных измерений.
; n - число выполненных измерений.
По своим свойствам, характеру возникновения и влияния на результаты измерений, их функции, погрешности подразделяют на грубые, систематические и случайные.
Грубые погрешности (промахи) возникают вследствие невнимательности наблюдателя, неисправности прибора, несоблюдении технологии работ, не учёта влияния изменяющихся
внешних условий: температуры, ветра, видимости и т.п. Обнаружить грубые погрешности можно, используя геометрические свойства наблюдаемого объекта (например, сумму внутренних углов плоского многоугольника), а также выполнением повторных измерений. Так, например, при линейных измерениях, пропуск целого пролета, равного длине мерного прибора, можно обнаружить измерением отрезка линии нитяным дальномером, иногда - даже шагами.
К систематическим относят такие погрешности результатов измерений, которые входят в эти результаты по определенному закону. Так, если известна длина меры при температуре 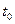 , а измерение длины линии местности выполнены при температуре
, а измерение длины линии местности выполнены при температуре 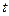 , то результат измерения длины линии будет содержать систематическую погрешность, пропорциональную разности температур
, то результат измерения длины линии будет содержать систематическую погрешность, пропорциональную разности температур 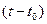 и длине линии. Влияние систематических погрешностей на результаты измерений исключают или сводят до пренебрегаемо малого значения выбором методики измерений или введением поправок в результаты.
и длине линии. Влияние систематических погрешностей на результаты измерений исключают или сводят до пренебрегаемо малого значения выбором методики измерений или введением поправок в результаты.
Случайные погрешности результатов измерений характеризуются тем, что при одинаковых условиях измерений они могут меняться по величине и знаку; их нельзя заранее предусмотреть, определить закон воздействия на результат.
- 30 -
Статистический анализ, т.е. анализ результатов больших рядов измерений, позволил для случайных погрешностей выявить ряд их свойств.
Первое свойство. Для данных условий измерений случайные погрешности по абсолютной величине не могут превосходить известного предела (свойство ограниченности), т.е.
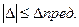 (4.2)
(4.2)
Второе свойство. Равные по абсолютной величине положительные и отрицательные случайные погрешности равновозможны, т.е. встречаются одинаково часто (свойство симметрии).
Третье свойство. Малые по абсолютной величине случайные погрешности при измерениях встречаются чаще, чем большие (свойство плотности).
Четвертое свойство. Среднее арифметическое из случайных погрешностей и их попарных произведений стремиться к нулю при
неограниченном возрастании числа измерений (свойство компенсации ), т.е.
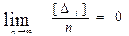 ;
; 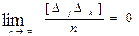 , (4.3)
, (4.3)
где 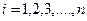 ;
; 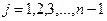 ;
; 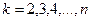 ;
;
n - число измерений; [ ]- Гауссов символ суммы.
4.3. Задачи теории погрешностей измерений
Как было отмечено выше, в результатах измерений неизбежно содержатся погрешности. Поэтому одной из задач теории погрешностей является изучение видов и свойств погрешностей измерений, причин их возникновения. Далее, выполнив измерения, всегда стремятся определить точность полученных результатов. Поэтому в теории погрешностей измерений устанавливаются критерии для оценки точности результатов измерений. Так как результаты измерений вследствие влияния погрешностей разнятся между собой, то возникает задача отыскания наиболее точного по вероятности значения определяемой величины из результатов многократных ее измерений.
Во многих случаях геодезической практики по результатам измерений вычисляют другие интересующие нас величины. Например, измерив сторону треугольника и два его угла, можно по известным формулам вычислить третий угол и две другие стороны.
- 31 -
В таких случаях результаты вычислений являются функциями измеренных величин. По указанной причине, перед теорией погрешностей возникает задача оценки точности функций измеренных величин.
Перечисленные задачи, которые решаются теорией погрешностей измерений, имеют большое значение для правильной организации, проведения геодезических работ и использования их результатов.
Кроме того, теория погрешностей геодезических измерений позволяет обоснованно выбрать необходимые для измерений приборы и инструменты, рассчитать ожидаемую точность измерений и окончательного результата, правильно выбрать метод обработки результатов измерений.
4.4. Равноточные измерения
4.4.1. Вычисление наиболее точного по вероятности значения
результата измерений одной и той же величины
Пусть некоторая величина, истинное (точное) значение которой
равно X, измерена равно точно n раз и получены результаты этих измерений: 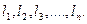 Составим разности
Составим разности
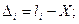 (4.4)
(4.4)
где 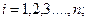 ;
; 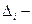 истинные случайные погрешности результатов liизмерений, т.е. уклонения результатов измерений от истинного (точного) значения измеряемой величины.
истинные случайные погрешности результатов liизмерений, т.е. уклонения результатов измерений от истинного (точного) значения измеряемой величины.
Найдем сумму уравнений (4.4) и разделим ее на число измерений.
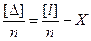 . (4.5)
. (4.5)
Введем обозначения:
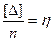 ; (4.6)
; (4.6)
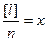 . (4.7)
. (4.7)
Величину 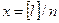 называют простой арифметической серединой или средним арифметическим из результатов
называют простой арифметической серединой или средним арифметическим из результатов 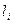 равноточных измерений.
равноточных измерений.
- 32 -
Выражение 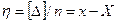 - есть истинная случайная погрешность простой арифметической середины, т.е. это уклонение простой арифметической середины от истинного (точного) значения
- есть истинная случайная погрешность простой арифметической середины, т.е. это уклонение простой арифметической середины от истинного (точного) значения 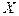 измеряемой величины.
измеряемой величины.
По четвертому свойству случайных погрешностей
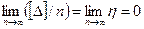 , (4.8)
, (4.8)
значит 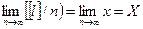 . (4.9)
. (4.9)
Таким образом, среднее арифметическое из результатов 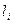 равноточных измерений стремится к истинному (точному) значению
равноточных измерений стремится к истинному (точному) значению 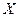 измеряемой величины при неограниченном возрастании числа измерений. Величину
измеряемой величины при неограниченном возрастании числа измерений. Величину 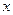 называют еще вероятнейшим значением измеряемой величины.
называют еще вероятнейшим значением измеряемой величины.
4.4.2. Оценка точности результатов ряда равноточных измерений.
В качестве критерия при оценке точности результатов геодезических измерений принята предложенная К.Ф. Гауссом средняя квадратическая погрешность, вычисляемая по формуле 
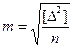 , (4.10)
, (4.10)
где Δ - истинная случайная погрешность результата, n - число измерений.
По величине средней квадратической погрешности можно определить предельную погрешностьΔпред., возможную для данного ряда измерений. В качестве предельной погрешности в геодезии принимают удвоенную среднюю квадратическую погрешность
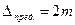 . (4.11)
. (4.11)
Если в ряду случайных погрешностей результатов равноточных измерений встречаются такие, которые по абсолютной величине превышают предельную, то такие погрешности считают грубыми. Измерения, в которых обнаружены эти погрешности, выполняют заново.
В ряде случаев для суждения о точности измерений недостаточно знания лишь абсолютного значения средней квадратической погрешности.
- 33 -
Например, измерены три отрезка линий местности:
L 1 = 240 м с погрешностью m 1 = ± 0,15 м;
L 2 = 600 м с погрешностью m 2 = ± 0,53 м;
L 3 = 500 м с погрешностью m 3 = ± 0,29 м.
Если сравнивать средние квадратические погрешности, то наиболее точно измерен первый отрезок. Однако, здесь следует учитывать и длину измеряемого отрезка, т.е. отнести погрешность к величине длины самого отрезка. В подобных случаях вводят понятие относительной погрешности, под которой понимают отношение абсолютной величины средней квадратической погрешности m к значению результата l измеряемой величины, т.е.
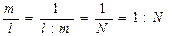 (4.12)
(4.12)
где 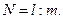
Для нашего примера относительные погрешности равны:

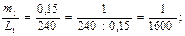

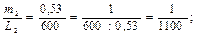
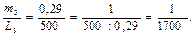
Сравнивая дроби, видим, что третье измерение является самым точным. В значении абсолютной величины средней квадратической погрешности и в знаменателе относительной погрешности следует удерживать две - три значащие цифры.
Вероятнейшие погрешности. Формула (4.10) К.Ф. Гаусса для средней квадратической погрешности справедлива в том случае, когда результаты  измерений сравниваются с истинным (точным) значением
измерений сравниваются с истинным (точным) значением  этой величины. В большинстве случаев практики топографо-геодезических и маркшейдерских работ истинное значение измеряемой величины неизвестно и поэтому используют вероятнейшее значение его
этой величины. В большинстве случаев практики топографо-геодезических и маркшейдерских работ истинное значение измеряемой величины неизвестно и поэтому используют вероятнейшее значение его 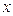 , определяемое по формуле (4.7). В этом случае среднюю квадратическую погрешность результата отдельного измерения ряда равноточных измерений определяют по вероятнейшим погрешностям.
, определяемое по формуле (4.7). В этом случае среднюю квадратическую погрешность результата отдельного измерения ряда равноточных измерений определяют по вероятнейшим погрешностям.
Пусть 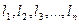 - результаты равноточных измерений одной и
- результаты равноточных измерений одной и
- 34 -
той же величины, 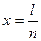 - простая арифметическая середина.
- простая арифметическая середина.
Составим разности 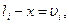 (4.13)
(4.13)
где 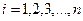 ;
; 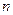 - число измерений;
- число измерений;
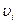 - вероятнейшие погрешности результатов
- вероятнейшие погрешности результатов 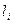 измерений т.е. уклонения значений каждого результата
измерений т.е. уклонения значений каждого результата 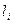 от простой арифметической середины, от вероятнейшего значения
от простой арифметической середины, от вероятнейшего значения 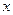 измеряемой величины. Найдём сумму уравнения (4.13) и разделим на их число
измеряемой величины. Найдём сумму уравнения (4.13) и разделим на их число
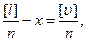 (4.14)
(4.14)
но 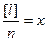 , тогда
, тогда
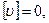 (4.15)
(4.15)
т.е. сумма вероятнейших погрешностей результатов равноточных измерений равна нулю при любом числе измерений.
Составим разности уравнений (4.1) и (4.13)
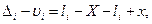 (4.16)
(4.16)
но, 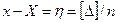 - истинная случайная погрешность простой арифметической середины, тогда
- истинная случайная погрешность простой арифметической середины, тогда
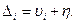 (4.17)
(4.17)
Выражение (4.17) есть уравнение связи истинных и вероятнейших погрешностей результатов равноточных измерений.
Возведем уравнения (4.17) в квадрат, сложим и разделим на их число
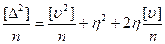 (4.18)
(4.18)
Но 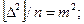
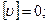
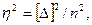
тогда 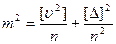 . (4.19)
. (4.19)
- 35 -
Второй член правой части уравнения ( 4.18 ) запишем в виде
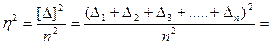
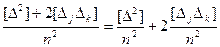 , (4.20)
, (4.20)
но 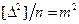 ;
; 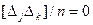 - по четвертому свойству случайных погрешностей.
- по четвертому свойству случайных погрешностей.
Уравнение (4.19) с учетом (4.20) примет вид
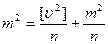 (4.21)
(4.21)
или 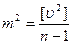 . (4.22)
. (4.22)
Окончательно
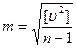 . (4.23)
. (4.23)
Выражение (4.23) является формулой Бесселядля средней квадратической погрешности результата отдельного измерения ряда равноточных измерений одной величины.
Практические рекомендации по вычислению простой арифме-тической середины.
1.Выбирают приближенное значение 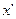 простой арифметической середины, в качестве которого лучше всего взять наименьшее из результатов
простой арифметической середины, в качестве которого лучше всего взять наименьшее из результатов 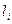 измерений, т.е.
измерений, т.е.
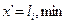 . (4.24)
. (4.24)
2. Находят разности
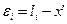 . (4.25)
. (4.25)
3. Вычисляют простую арифметическую середину
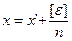 . (4.26)
. (4.26)
- 36 -
4.4.3. Оценка точности функций измеренных величин
В большинстве случаев практики топографо-геодезических и маркшейдерских работ искомые величины получают в результате вычислений как функции измеренных величин. Полученные при этом результаты будут содержать погрешности, которые зависят как от погрешностей аргументов (измеренных величин), так и от вида функций. Возникает задача оценки точности функций измеренных аргументов.
Средняя квадратическая погрешность функции общего вида
Дана функция
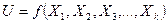 , (4.27)
, (4.27)
где 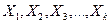 - точные (истинные) значения измеряемых величин.
- точные (истинные) значения измеряемых величин.
Пусть в результате измерений получены приближенные значения 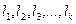 этих величин.
этих величин.
Тогда 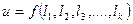 (4.28)
(4.28)
- приближенное значение функции 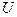 .
.
Составим разность уравнений (4.27) и (4.28)
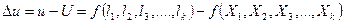 , (4.29)
, (4.29)
которая является истинной случайной погрешностью функции 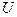 .
.
Разности 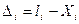 , (4.30)
, (4.30)
- суть истинные случайные погрешности аргументов 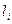 ,
, 
Тогда
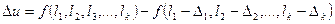 . (4.31)
. (4.31)
Чтобы найти линейную зависимость между погрешностями аргументов и погрешностью функции, продифференцируем функцию (4.28).
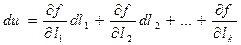 , (4.32)
, (4.32)
где 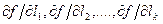 - частные производные функции по каждому из аргументов. Заменим в выражении (4.32) дифференциалы истинными случайными погрешностями функции и аргументов
- частные производные функции по каждому из аргументов. Заменим в выражении (4.32) дифференциалы истинными случайными погрешностями функции и аргументов
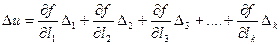 . (4.33)
. (4.33)
- 37 -
При многократном измерении аргументов, например n раз, получим
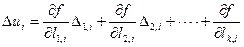 , (4.34)
, (4.34)
где 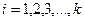 .
.
Производные функции по соответствующим аргументам в разных измерениях практически остаются постоянными и могут быть вычислены по приближенным значениям аргументов 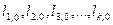 , в качестве которых можно взять
, в качестве которых можно взять
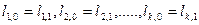 , т.е. значения аргументов, полученные при первом измерении определяемых величин.
, т.е. значения аргументов, полученные при первом измерении определяемых величин.
В соответствии с этим можно принять
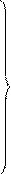

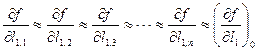 ,
,
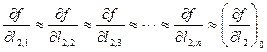 , (4.35)
, (4.35)
…………………………………………………
…………………………………………………
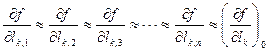 .
.
С учетом (4.35) выражение (4.34) примет вид
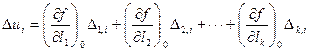 (4.36)
(4.36)
Возведем уравнения (4.36) в квадрат, сложим и разделим на их число
- 38 -
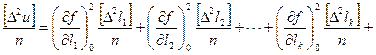
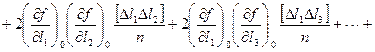
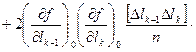 (4.37)
(4.37)
На основании (4.3) и (4.10) можно записать
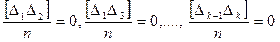
и 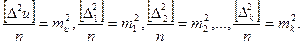 (4.38)
(4.38)
Выражение (4.37) с учетом (4.38) примет вид
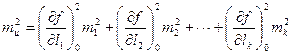 (4.39)
(4.39)
или 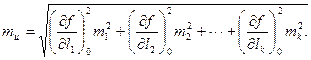 (4.40)
(4.40)
Таким образом, средняя квадратическая погрешность функции независимых аргументов равна корню квадратному из суммы квадратов произведений частных производных функции по каждому из аргументов на средние квадратические погрешности соответствующих аргументов.
- 39 -
Средняя квадратическая погрешность простой арифметической середины
Формулу (4.7) для простой арифметической середины перепишем в виде
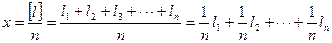 , (4.41)
, (4.41)
где 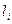 - результаты равноточных измерений одной и той же вели-чины; i = 1, 2, 3,..., n; n - число измерений.
- результаты равноточных измерений одной и той же вели-чины; i = 1, 2, 3,..., n; n - число измерений.
На основании (4.39) имеем
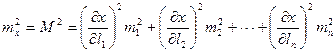 ,
,
но 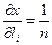 , тогда
, тогда
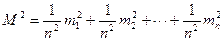 . (4.42)
. (4.42)
Так как измерения равноточные, т.е. 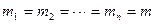 .
.
Средняя квадратическая погрешность простой арифмети-ческой середины в 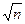 раз меньше средней квадратической погрешности результата каждого отдельного измерения.
раз меньше средней квадратической погрешности результата каждого отдельного измерения.
Следовательно, выражение (4.42) примет вид
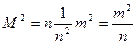 , (4.43)
, (4.43)
откуда 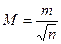 (4.44)
(4.44)
Сравнивая формулу (4.43) и второй член правой части уравнения (4.21), можно сделать вывод, что
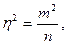
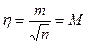 , (4.45)
, (4.45)
т.е. истинная случайная погрешность простой арифметической середины равна средней квадратической погрешности простой арифметической середины.
- 40 -
Оценка точности результатов угловых измерений
в триангуляции
Триангуляция - плановая геодезическая сеть, состоящая из треугольников (см. рис. 4.1), в которой измерены все внутренние углы треугольников и одна или несколько сторон - базисов. Вершины треугольников - пункты сети, положение (координаты) которых подлежат определению. Известно, что сумма внутренних углов плоского треугольника равна 180° ,
т.е. 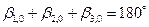 , (4.46)
, (4.46)
где 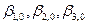 - истинные (точные) значения углов.
- истинные (точные) значения углов.
Пусть 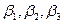 - результаты измерения этих углов, т.е. приближенные значения углов.
- результаты измерения этих углов, т.е. приближенные значения углов.
Тогда, согласно (4.1), имеем
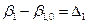 ,
,
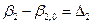 , (4.47)
, (4.47)
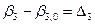
- истинные случайные погрешности результатов измерений.
Перепишем равенство (4.46) с учетом формул (4.47)

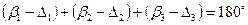 ; (4.48)
; (4.48)
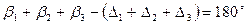 ; (4.49)
; (4.49)
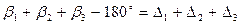 . (4.50)
. (4.50)
Обозначим
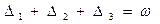 . (4.51)
. (4.51)
ω - называют угловой невязкой в треугольнике, т.е. это истинная случайная погрешность суммы внутренних углов треугольника.
Тогда уравнение (4.50) можно записать в виде
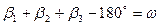
 (4.52)
(4.52)
или 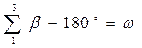 (4.53)
(4.53)
Пусть равно точно измерены углы в 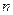 треугольниках, для каждого из которых справедливы равенства (4.51), т.е.
треугольниках, для каждого из которых справедливы равенства (4.51), т.е.
- 41 -
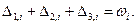 (4.54)
(4.54)
где 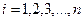 - номера треугольников.
- номера треугольников.
Возведем уравнения (4.54) в квадрат, сложим и разделим на их число
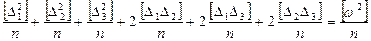 . (4.55)
. (4.55)
На основании (4.3) и (4.10) можно записать
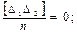
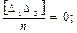
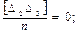
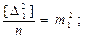
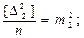
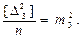
Тогда
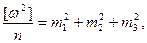 (4.56)
(4.56)
где 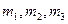 - средние квадратические погрешности результатов измерений углов
- средние квадратические погрешности результатов измерений углов 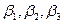 в каждом из треугольников.
в каждом из треугольников.
Так как измерения равноточные, т.е. 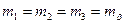 , то
, то
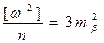 (4.57)
(4.57)
или 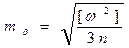 (4.58)
(4.58)
Это формула Ферреро, по которой обычно выполняется оценка точности результатов измерений горизонтальных углов в триангуляции.
4.4.4. Оценка точности результатов ряда двойных равноточных измерений
Очень часто в практике геодезических и маркшейдерских работ искомую величину определяют по результатам двукратных равноточных измерений этой величины. Например, горизонтальные углы измеряют двумя полуприемами, превышение на станции при геометрическом нивелировании определяется по черным и красным сторонам реек, длины отрезков линий местности находят из результатов измерений этих отрезков в прямом и обратном направлениях.
- 42 -
Возникает задача оценки точности этих результатов. Имеем ряд величин, истинные значения которых равны
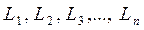 . (4 .59)
. (4 .59)
Пусть каждая из этих величин измерена равно точно дважды и получены результаты:
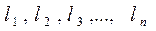 ; (4.60)
; (4.60)
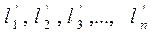 , (4.61)
, (4.61)
Составим разности между результатами измерений и их истинными значениями:
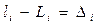 ; (4.62)
; (4.62)
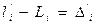 , (4.63)
, (4.63)
где 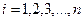 . Найдем разности уравнений (4.62) и (4.63)
. Найдем разности уравнений (4.62) и (4.63)
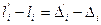 (4.64)
(4.64)
и обозначим 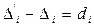 . (4.65)
. (4.65)
Здесь 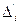 и
и 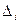 - истинные случайные погрешности результатов.
- истинные случайные погрешности результатов.
Возведем уравнения (4.65) в квадрат, сложим и разделим на их число
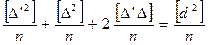 . (4.66)
. (4.66)
На основании (4.3) и (4.10) запишем
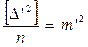 ;
; 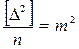 ;
; 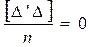 ,
,
тогда 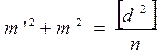 . (4.67)
. (4.67)
Так как измерения равноточные, т.е. 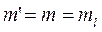 , то
, то
- 43 -
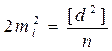 ,
, 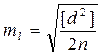 . (4.68)
. (4.68)
При двойных равноточных измерениях за окончательное значение принимают среднее арифметическое из результатов отдельных измерений, т.е. 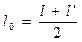 ,
,
тогда 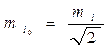 или
или 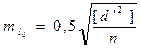 . (4.69)
. (4.69)
Формулы (4.68) и (4.69) справедливы лишь в том случае, если разности 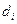 не содержат систематических погрешностей.
не содержат систематических погрешностей.
Пусть разности содержат систематическую погрешность 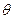 , т.е.
, т.е.
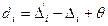 . (4.70)
. (4.70)
Сложим уравнения (4.70) и разделим на их число
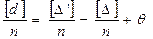 . (4.71)
. (4.71)
На основании четвертого свойства случайных погрешностей имеем
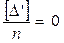 ,
, 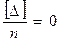 ,
,
т.е. 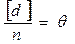 . (4.72)
. (4.72)
Среднее арифметическое из разностей результатов двойных равноточных измерений отлично от нуля и численно равно систематической погрешности этих результатов.
Вычтем из каждой разности 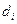 величину систематической погрешности
величину систематической погрешности 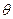 , т.е. образуем новые разности
, т.е. образуем новые разности
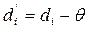 . (4.73)
. (4.73)
Сложив равенства (4.73) и поделив их на n, получим
- 44 -
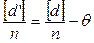 , но
, но 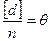 , тогда
, тогда
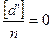 , (4.74)
, (4.74)
т.е. среднее арифметическое из разностей результатов двойных равноточных измерений, свободных от систематических погрешностей, всегда равно нулю.
Разности 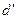 , как уклонения
, как уклонения 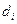 от простой арифметической середины и обладающие свойством
от простой арифметической середины и обладающие свойством 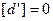 , можно считать вероятнейшими погрешностями разностей
, можно считать вероятнейшими погрешностями разностей 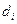 . Применяя к ним формулу Бесселя для средней квадратической погрешности, запишем
. Применяя к ним формулу Бесселя для средней квадратической погрешности, запишем
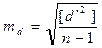 , (4.75)
, (4.75)
а 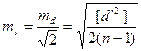 . (4.76)
. (4.76)
Средняя квадратическая погрешность среднего арифметического из результатов 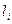 и
и 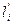 будет равна
будет равна
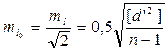 . (4.77)
. (4.77)
Вычисление значения числителя подкоренного выражения можно проконтролировать по формуле
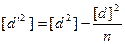 . (4.78)
. (4.78)
Примечание. Оценку точности по разностям результатов двойных равноточных измерений следует выполнять по формулам (4.68) и (4.69), если разности удовлетворяют условию
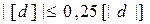 , (4.79)
, (4.79)
в противном случае, по формулам (4.75) - (4.77).
- 45 -
4.4.5. Примеры оценки точности результатов равноточных измерений одной величины и функций независимо измеренных величин
Задача №1. По результатам равноточных измерений горизон-тального угла девятью приемами (см. табл. 4.1) найти наиболее точное по вероятности значение угла, средние квадратические погрешности измерения каждого отдельного угла и простой арифметической середины.
Вычисления выполняют в следующей последовательности.
1. Выбирают приближенное значение 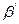 простой арифметической середины как наименьшее из результатов измерений, т.е.
простой арифметической середины как наименьшее из результатов измерений, т.е. 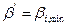 В нашем примере это значение равно
В нашем примере это значение равно 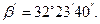
2. Вычисляют уклонения 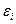 результатов измерений
результатов измерений 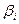 от этого приближенного значения
от этого приближенного значения 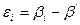 и сумму этих уклонений
и сумму этих уклонений
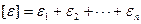
3. В колонке (4) вычисляют квадраты 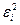 и их сумму
и их сумму 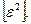
4. По формуле (4.26) вычисляют простую арифметическую середину 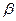 - наиболее точное по вероятности значение измеряемого угла.
- наиболее точное по вероятности значение измеряемого угла.
5. Находят вероятнейшие погрешности 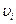 как разности результатов отдельных измерений и округленного значения
как разности результатов отдельных измерений и округленного значения 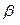 , т.е.
, т.е.
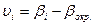 ,
,
их сумму 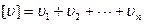
с контролем 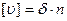 ,
,
где 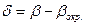 - погрешность округления среднего арифметического.
- погрешность округления среднего арифметического.
6. В колонке (6) вычисляют квадраты вероятнейших погрешностей 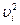 и их сумму
и их сумму
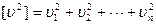
с контролем 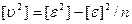 .
.
7. По формуле (4.23) Бесселя вычисляют среднюю квадратическую погрешность результата каждого отдельного измерения
- 46 -
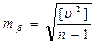 .
.
8. По формуле (4.44) находят среднюю квадратическую погрешность простой арифметической середины
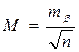 .
.
9. Окончательный результат записывают в виде
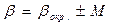 .
.
Задача №2. В каждом треугольнике микротриангуляции (рис. 4.1) измерено одинаково точно по три внутренних горизонтальных угла (см. табл. 4.1). Вычислить среднюю квадратическую погрешность результатов измерений каждого отдельного угла, применив формулу Ферреро
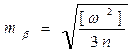 ,
,
где 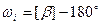 - угловые невязки в треугольниках, n – число треугольников.
- угловые невязки в треугольниках, n – число треугольников.
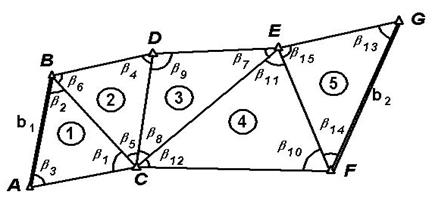
Рис. 4.1. Схема сети микротриангуляции
- 47 -
Таблица 4.1
 Оценка точности результатов измерения отдельного горизонтального угла
Оценка точности результатов измерения отдельного горизонтального угла
| Номера приемов i | Результаты измерений βi | εi | εi2 |
|
| Основные формулы, вспомогательные вычисления |
| 5 | 6 | |||||
| 32o 23´ 44" | + 4 | -0,6" | 0,36 | 1. 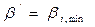
| ||
| -4,6 | 21,16 | 2. 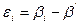
| ||||
| + 3 | -1,6 | 2,56 | 3. 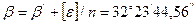
| |||
| + 5 | +0,4 | 0,16 | ||||
| + 6 | +1,4 | 1,96 | 4. 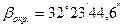
| |||
| + 3 | -1,6 | 2,56 | ||||
| + 8 | +3,4 | 11,56 | 5. 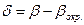
| |||
| + 5 | +0,4 | 0,16 | ||||
| 32o 23´ 47" | + 7 | +2,4 | 5,76 | 6. 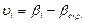 
| ||
| ∑ | + 42 | -0,4 | 46,20 | 7. 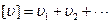
| ||
| β´ β β окр. | 32o 23´ 40" 32o23’44,56" 32o 23´ 44,6" | [ε]2=1681 mβ = ± 2,4" ; M = ± 0,80" Окончательный результат : β = 32º 23´ 44,6" ± 0,80" | Контроль: 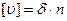
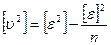 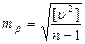
|
Таблица 4.2
Обработка результатов угловых измерений в микротриангуляции
| Названия углов | Номера треугольников и значения измеренных углов | ||||
| 80°07,7’ | 74°21,6’ | 36°39,2’ | 39°17,4’ | 69°49,6’ |
| 50 58,3 | 64 35,5 | 71 49,6 | 96 15,8 | 36 39,2 |
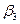
| 48 53,1 | 41 01,8 | 71 32,6 | 44 26,1 | 73 32,4 |
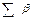
| 179°59,1’ | 179°58,9’ | 180°01,4’ | 179°59,3’ | 180°01,2’ |
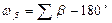
| - 0,9’ | - 1,1’ | + 1,4’ | - 0,7’ | + 1,2’ |
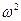
| 0,81 | 1,21 | 1,96 | 0,49 | 1,44 |
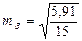 =
= 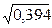 = ± 0,63'
= ± 0,63'
Задача №3. В теодолитном ходе равно точно измерено 11 горизонтальных углов, каждый со средней квадратической погрешностью 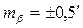 . Определить среднюю квадратическую и предельную погрешности суммы этих углов.
. Определить среднюю квадратическую и предельную погрешности суммы этих углов.
Имеем функцию 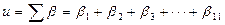 .
.
Частные производные ее по каждому из аргументов равны 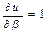 .
.
Тогда 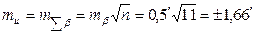 ;
;
и 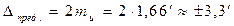 .
.
Задача №4. Горизонтальный угол β (см. рис. 4.2) измерен теодолитом 2Т30 одним полным приемом способом «приемов».
Определить среднюю квадратическую погрешность среднего арифметического из значений результатов измерений угла в полуприемах, если средняя квадратическая погрешность отсчетов по лимбу составила 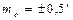 .
.
Дата добавления: 2021-07-22; просмотров: 566;











