Определение погрешностей моделирования (оценки средней вероятности ошибки) методом малых отклонений

Рассматривается методика, позволяющая установить соответствие между погрешностями моделирования параметров стохастического канала и отличием средней вероятности ошибки (СВО) СПДИ, полученной на модели канала, от величины СВО для его гипотетической модели.

Поставленная задача решается расчетно-аналитическим методом, использующим разложение в ряды.

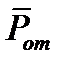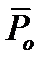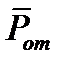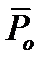Допустим, что для рассматриваемой реализации модели канала средняя вероятность ошибки при исследовании СПДИ отличается от значения средней вероятности ошибки , полученной на гипотетической модели. В качестве меры различия величин и можно принять некоторую функцию потерь 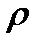. Например:

1) модульная функция потерь

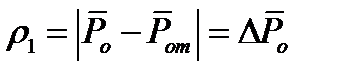; (11.1)

2) нормированная модельная функция потерь

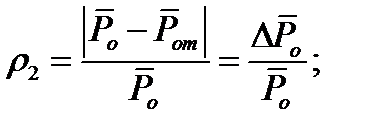(11.2)

3) квадратичная функция потерь

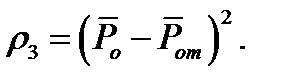(11.3)

Величину 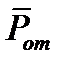будем считать не случайной в каждом эксперименте, поскольку она получена для конкретной реализации модели. В противном случае необходимо рассматривать среднее значение функции потерь .

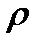Целесообразность введения меры адекватности на более низком иерархическом уровне, например, по адекватности энергетических или статистических характеристик модели и канала, показана в работе [].

Поскольку средняя вероятность ошибки для заданных способов приема и вида модуляции является функцией параметров сигнала на выходе канала.

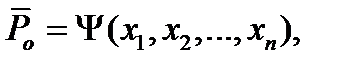(11.4)

то для величины можно записать

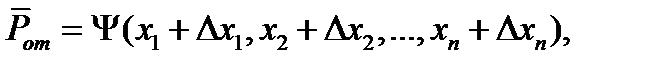(11.5)

где 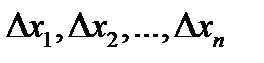– абсолютные погрешности моделирования отдельных параметров сигнала.

Представляя 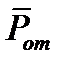рядом Тейлора и полагая отклонения параметров 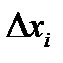малыми, получим

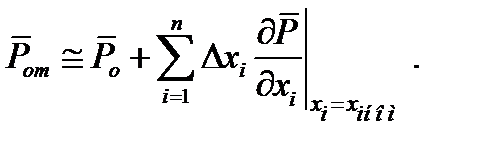(11.6)

Учет следующих членов ряда Тейлора вызывает увеличение объема вычислений, но не гарантирует получения существенно большей точности.

Относительная погрешность средней вероятности ошибки

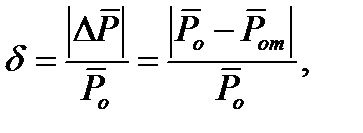
или с учетом (11.6)

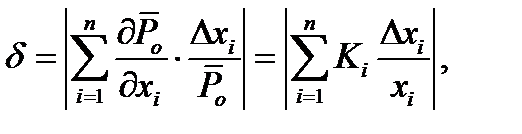(11.7)

где

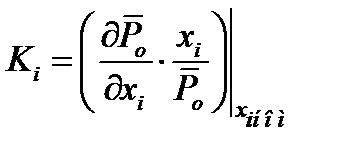(11.8)

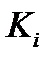– коэффициент влияния i-го параметра [], который характеризует степень влияния погрешности моделирования i-того параметра канала на общую погрешность (11.7).

Выражение (11.7) является приближенным, справедливым для достаточно малых отклонений 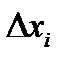и гладких функций .

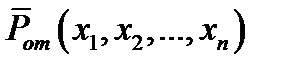Если известен интервал значений 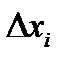, то максимальная погрешность

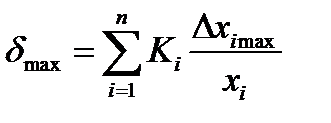(11.9)

соответствует такой ситуации, когда параметры всех элементов имеют максимальные по величине и такие по знаку отклонения, при которых возникает наибольшее по абсолютному значению отклонение величины .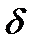

Часто 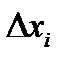являются случайными величинами. Как показано в [] использование выражения (11.9) при определении погрешности оценки СВО целесообразно при бимодальном распределении каждого из параметров .

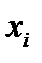При известных коэффициентах влияния 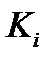, определенных аналитически в соответствии с (11.8) при известном выражении (11.4), либо экспериментально, можно сформулировать ограничения на значения допусков погрешностей при моделировании параметров 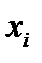с целью обеспечения заданной погрешности .

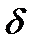При унимодальном распределении величин 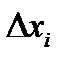для определения погрешности 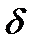целесообразно использовать метод моментов []. При этом определяются среднее значение ошибки

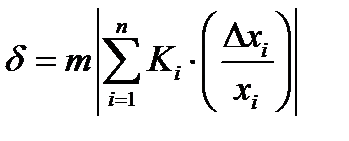(11.10)

и ее дисперсия

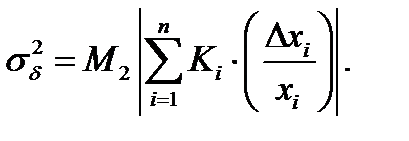(11.11)

Если допуски на ошибки параметров 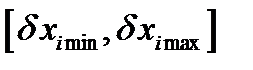известны или заданы, то можно использовать вероятностную меру погрешности 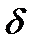. Вероятность попадания величины 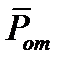в пределы 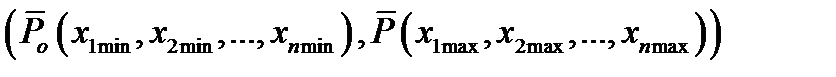при независимых 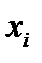и монотонной зависимости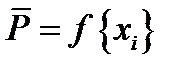

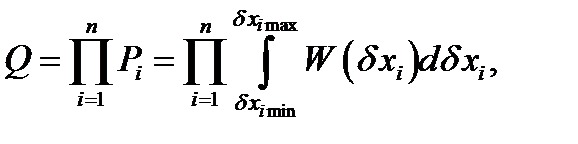(11.12)

где 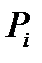– вероятность нахождения ошибки i-го параметра в интервале ;

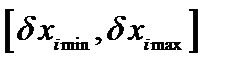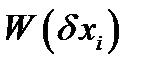– распределение ошибки .

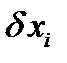Поскольку все расчеты, основанные на методе малых отклонений, предполагают знание коэффициентов чувствительности 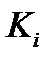, оценивающих влияние относительных отклонений 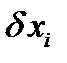параметра на относительное отклонение 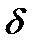СВО, остановимся на методах расчета коэффициентов влияния .

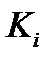1. Если известно аналитическое выражение средней вероятности ошибки, получаемой для исследуемой системы на математической модели, то расчет коэффициентов влияния производится по формуле (11.8).

2. При отсутствии аналитического выражения, связывающего среднюю вероятность ошибки с параметрами модели, очевидным примером для расчета 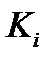является вычисление 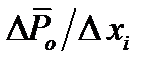при достаточно малой величине приращения 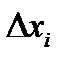. При наличии реальной СПДИ и макетно-агрегатной модели канала отношение 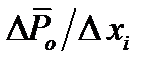может быть оценено путем изменения значения параметра 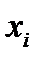на величину 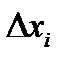и определения возникающего при этом отклонения .

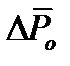3. Если отсутствует аналитическое выражение для 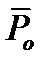и для исследуемой СПДИ составлен лишь алгоритм обработки сигнала, то определение коэффициентов влияния на основании отношения 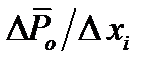можно возложить на компьютер, заложив в программу модель канала и алгоритм обработки сигнала и определяя для каждого 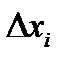(при номинальных значениях всех остальных параметров) величину .

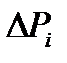Если величины 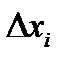являются случайными и известны их распределения, то с помощью компьютера можно найти распределение величины 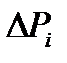, а также вероятность попадания случайной величины 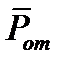в заданные пределы. Для этого используется метод случайных испытаний (метод Монте-Карло).

Таким образом, использование метода малых отклонений при оценке влияния погрешностей моделирования параметров канала на погрешность получаемой СВО позволяет обосновать требования к точности моделирования этих параметров.

Метод малых отклонений позволяет определять степень влияния на ОСВО только тех параметров канала, которые являются определяющими для 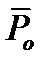и исключают из рассмотрения несущественные с этой точки зрения параметры, упрощая тем самым процесс моделирования.