СТРУКТУРА, СТРУКТУРИЗАЦИЯ, МЕТАОПЕРАЦИЯ

Структурность окружающего мира проявляется в единст­ве прерывности и непрерывности. Структурные уровни матери­альных систем простираются от элементарных частиц и полей до галактик и систем галактик, от отдельных молекул и живых клеток до организмов и их сообществ.

Структура предметной области (объекта наблюдений) оп­ределяется совокупностью устойчивых связей его элементов, обеспечивающих целостность и тождественность самому себе, т.е. то, что обеспечивает сохранение основных свойств при раз­личных внешних и внутренних изменениях [5].

Задача структуризации состоит в определении элементов структуры и их отношений, сохраняющих системные свойства, присущие объекту (предметной области).

Граф, как система элементов (вершин) и их отношений (ребер), является наиболее абстрактной формой представления каркаса структуры предметной области.

Размеченный и означенный граф служит моделью пред­метной области.

Для примера рассмотрим граф-схему представления ра­циональной системы, на основе которой субъект может моде­лировать поведение эмпирической системы наблюдений в зада­че о двух сигналах. Рациональная система открыта для расши­рения и приведена в приложении П.3.

Рациональные системы в приложении П3 представляют собой набор формул {Ф_i}, связанных отношением "выводимости" или "следования". Каждая Ф_i, тоже система по определению, элементами которой являются аргументы, а от­ношения определяются алгебраическими и реляционными опе­рациями.

Система Ф_i может быть представлена как ненаправленная (предикатная форма записи вида Ф_i @ 0) или направленная (функциональная форма записи, частный случай предикатной формы).

Например, для реляционной операции поиска макси­мума имеем:

Ф₁ @ 0: | X_i | - max { X_i } = 0. (8.1)

{х₁;....х_n} - порождающие переменные;

| X |- порождаемая переменная;

max X - оператор порождения, реляционная операция выбора максимального значения x_max Î Х.

В случае алгебраической операции, например: у = b₀+b₁Х, имеем: Ф₄ = 0 Û у- b₀-b₁Х = 0.

	x		Y = f(x)

направленная система;

			Ф4

ненаправленная.

Конституэнты b₀ и b₁ определяются по методу наимень­ших квадратов (см.П.3).

Рассмотрим структурные блоки системы {Ф₀;Ф₁₁} для за­дачи "Сигнал".

Блок 1 - формирование исходных данных:

Ф₀ ® Ф₁ ® Ф₀ / Ф₁ = 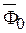. Здесь 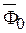- нормированные значения сиг­нала, т.е. {x_i / x_max } =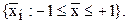

Блок 2 - вычисление по формулам Ф₂; Ф₃; Ф₄; Ф₁₁ из данных Ф₀ или Ф₁. Здесь процесс интегрирования заменяется суммированием по методу трапеций.

Блок 3 - тригонометрическая аппроксимация данных ря­дами Фурье, формулы Ф₅, Ф₆, Ф₇, Ф₈, Ф₉, Ф₁₀, Ф₁₁.

Блок 4 - определение метахарактеристик объекта от из­менения фактора F:

F Î { F₀; F₁; F₂; …}.

Блоки 1, 2, 3 определены при конкретном значении F.

Структуризация системы на уровне первых трех блоков позволяет перейти к метасистемам блока 4.

Рассмотрим метасистемы Ф₂ и Ф₃ для вычисления метапараметров Х_эф и Х_ср. В общем случае для непрерывного сигна­ла имеем:

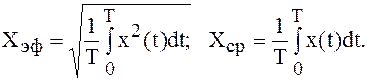(8.2)

Это функционалы, т. е. соответствия между множествами чисел с одной стороны (Х_эф; Х_срÎN) и множествами функций с другой стороны (х(t); х²(t)).

Гомоморфизм системы (8.2) заключается в том, что одно и то же значение (слева) может иметь множество различных функций х(t) (справа).

Другими словами, за счет неоднозначности отображения теряется информация о форме конкретного сигнала х(t).

При этом получается обобщенный параметр слева (метапараметр).

Подобные операции, связанные с невосстановимой поте­рей информации о форме сигнала х(t), относятся к классу метаопераций, а системы, реализующие гомоморфного типа опе­рации, метасистемами. В данном случае имеем метасистему по­рождения для поверхности отклика вида:

Х_эф = f(F) и Х_ср = f(F) при однократном эксперименте.

Отметим, что в основе вычислительного процесса для экспериментально полученной кривой х(t), лежат изоморфные преобразования типа оператора:

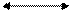
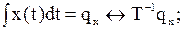(8.3)

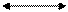x(t)

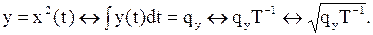
Оператор связывает одно множество функций с другим множеством функций . Введение связанных переменных в виде пределов интегрирования меняет математические свойства опе­рации :

-интегрирование в заданных пределах равносильно опре­делению конкретной площади;

-дифференцирование в заданной точке равносильно оп­ределению конкретной касательной;

-арность предикатной формы в логике предикатов снижа­ется на единицу по каждому связанному аргументу;

-ненаправленная форма представления системы транс­формируется в направленную.

-и т.п.

Операции, составляющие изоморфизм преобразований, называются опера­циями структуризации. При структуризации сохраняется переход от конкретного к конкретному в полном объеме. При метаоперации переход от конкретного к конкретному приобретает черты обобщения кон­кретного по выделенному свойству, выделение эквивалентных классов объектов по заданному свойству.

Если при наличии операции структуризации базис систе­мы остается без изменения, то получающиеся системы называ­ются структурированными. Двойственные по определению сис­темы называются метасистемами.

Для указанных операций и систем введем следующие ус­ловные обозначения:

сХ, mХ - однократная структуризация или метаоперация, в результате которой из системы ХÎ{I;D;F} получены структу­рированная или метасистема (исходная, данных, порождения).

С²Х, М²Х, СМХ, МСХ - двукратное последовательное применение указанных операций.

В принятой системе обозначений пошаговые преобразо­вания (8.3), направленные к вычислению параметров сигнала (8.1), можно определить в виде схемы "С-М" операций над X = {x_j}.

При конкретизации операций имеем :

С₁ - взятие неопределенного интеграла С₁Х = Q_x;

С₁^-1 - дифференцирование С₁ ^-1Х = Q_x;

С₂ - возведение в квадрат С₂Х = Q_у;

С₂^-1 - извлечение квадратного корня;

С₂^-1С₂ Q_у = X; и далее (см. рис. 8.1);

С₃ - умножение на параметр, в данном случае на Т^-1;

С₃^-1- деление на параметр;

С₄ - извлечение корня из данных на входе:

С₄ = С₂^0,5 ; С₄^-1 = С₂;

М₁ - метаоперация вычисления определенного интеграла на интервале [0;Т].

На рис. 8.1а тип (С или М) операции и ее конкретная форма указаны разметкой дуг. Уровень порождаемой системы и ее конкретное значение показаны разметкой вершины графа.

Упражнения

1. Форма нормированного сигнала х(t) определена на от­резке
–1 £ х(t) £ 1, известно значение Х_эф.

Требуется построить рациональную систему для опреде­ления Х_max в единицах измерения Х_эф.

2. Постройте план для двухфакторного эксперимента в случае
FÎ{ F₀; F₁...F_max} и Z_n= R_n={R₀; R₁;...R_max}.

а. Определите число испытаний по плану и в общем слу­чае при
FÎ {0,1,2,3,4,5}; R={0,1,3}.

б. Определите объем системы данных, получаемых с фо­тограмм, на каждой из которых записана система из двух сиг­налов i₁(t) и U₂(t) .

3. Постройте граф-схему и матрицу смежности для компо­зиций из операций структуризации и метаоперации для перехода от системы Х к системе Х_ср.

а. Для непрерывного методологического типа данных х(t)=Х.

б. Для дискретного методологического типа данных {х_j}, где х_jÎХ.

8.3. К ЗАДАЧЕ ПЕРЕЧИСЛЕНИЯ
МЕТОДОЛОГИЧЕСКИХ ТИПОВ СИСТЕМ

Абстрагируясь от конкретного содержания системологических операций {С_i} и {М_i}, решетку уровней структурированных и метасистем можно представить рис. 8.2.

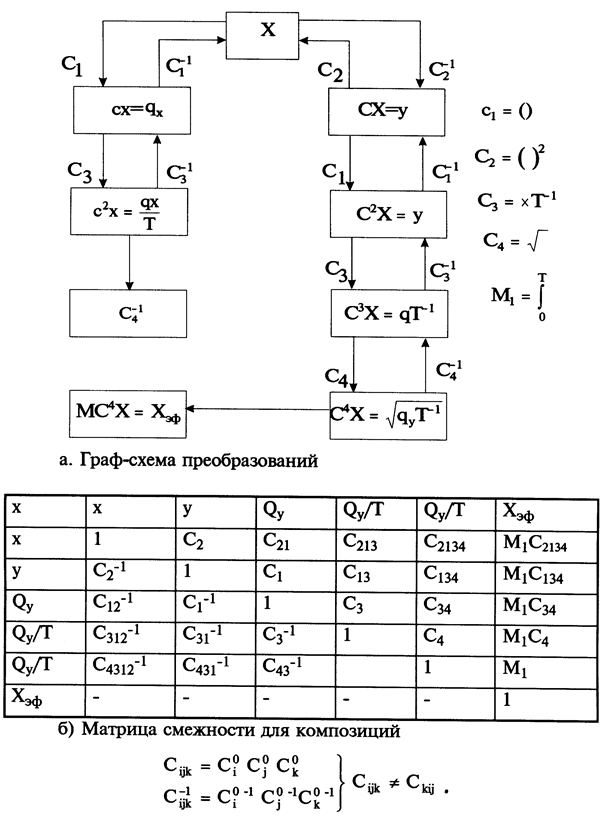
Рис. 8.1. Пример на применение операций структуризации и метаоперации над полем чисел X (для непрерывного сигнала X(t))

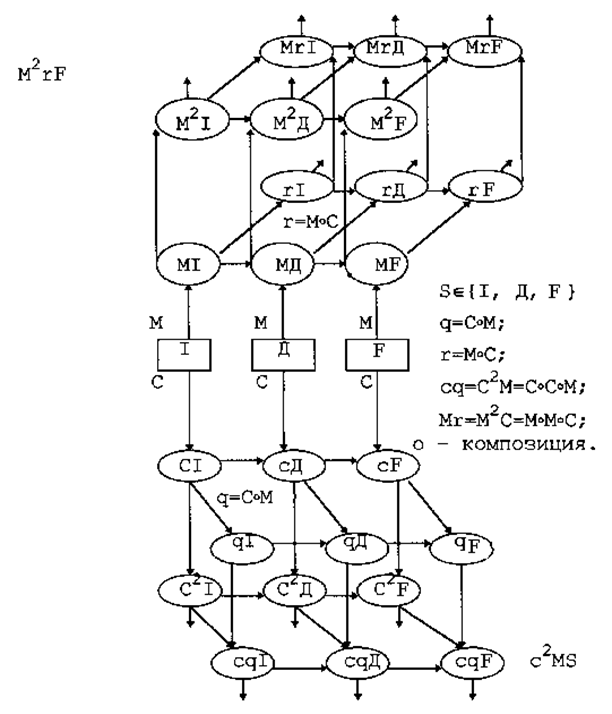
Рис. 8.2. Решетка структурированных уровней и метасистем порождения для X Ì {I, D, F}

Решетка имеет вид многослойной структуры. Первый слой определяет применение операций одного типа: унарных, бинар­ных ... и т.д.

Следующий слой отличается от предыдущего композицией операций С ° М = q и М ° С = r в соответствии с прави­лами образования первого слоя. Далее по индукции.

Проблема перечисления эпистемологических уровней опи­сания эмпирических систем решается с помощью изоморфизма математиче­ских свойств, присущих известным математическим моделям, а именно: треугольнику Паскаля, биномиальному ряду коэффици­ентов Ньютона, определению числа сочетаний на множестве N из М элементов.

Рис. 8.3 иллюстрирует процесс перечисления методологи­ческих типов систем, комбинируемых из исходного множества систем {I; D; F}путем многократного применения операций {C; M}.

ЗАКЛЮЧЕНИЕ

В настоящее время теория систем переживает новый этап своего развития, связанный с процессами создания систем зна­ний, с инженерией знаний. По своей сути наши знания являются общей системой по отношению к конкретным системам данных. Элементы знаний структурно связаны различными системами от­ношений. Это позволяет рассматривать знания как системы, а теорию систем как базовую науку инженерии знаний.

Изучение теории систем следует базировать на знании ис­тории возникновения и логике развития данного научного на­правления.

В списке литературы ряд книг содержит информацию исто­рического характера, связанную с процессом становления теории систем.

В [28, сс.79-109], например, имеется коммента­рий первоисточников с кратким историческим обзором. Здесь же рассматриваются различные подходы к математическому основанию общей теории сис­тем, кроме алгебраического. В [1] в примечаниях к каждой главе вынесена информация об авторах и их подходах при решении за­дач теории систем и системологии, как одного из вновь создавае­мых направлений в теории систем.

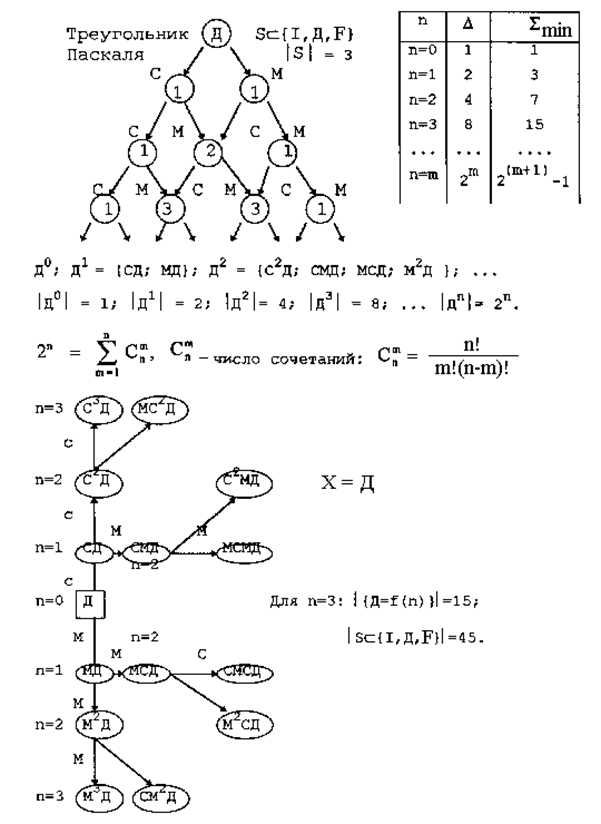
Рис. 8.3. Перечисление эпистемологических уровней системы

Не имея возможности в учебном пособии останавливаться на обзоре и анализе литературы, рекомендуем для самостоятель­ной проработки указанные два источника [1,28], через которые можно выйти в мир обширной библиографии по данной дисцип­лине.

Теория систем является научным направлением, при изучении которого остро ощущается недостаток в учебно-методической литературе.

В 1997 г. для студентов, обучающихся по специальности «Системный анализ в экономике и организации производства» подготовлен учебник по основам теории систем и системному анализу [31]. Учебник может служить справочным пособием для инженерных специальностей, связанных с проектированием сложных технических комплексов. Учебник содержит именной указатель и многостраничный список литературы, использованной авторами при написании учебника. Материалы учебника могут быть полезны и для специальности 220200.