Номинальная числовая апертура стекловолокна

Направим световой пучок на торец СВ так, как показано на рисунке 3.11. Пучок ограничен двумя крайними лучами 1 и 2. Луч 1 составляет угол g_к с осью симметрии СВ, луч 2 распространяется вдоль оси симметрии СВ.

Луч 1 преломляется на границе n_V ® n_С под углом b и превращается в луч 3. Соответствующая лучу 3 волна в точке B распадается на две, волна 4 преломляется в среду с АПП = n₀ под углом a, волна 5 отражается от границы n_С ® n₀.

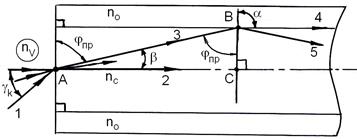
Рисунок 3.11 – Прохождение лучей в световоде

Назовем угол g_К – критическим и потребуем, чтобы ему соответствовал предельный угол падения j = j_ПР на границу раздела n_С ® n₀, как показано на рисунке 3.11. Тогда угол преломления 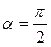и волна 4 скользит вдоль границы раздела n_С ® n₀. В окрестности точки A закон преломления света имеет вид: 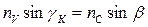, где n_v – АПП среды, из которой свет попадает на торец CB. Из треугольника ABC следует 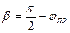; 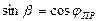. Следовательно

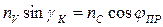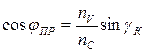, (3.12)

В окрестности точки B

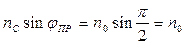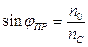, (3.13)

Возводя во вторую степень (3.12) и (3.13) складывая их почленно, имеем

, ,

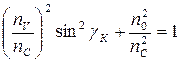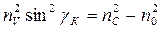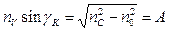. (3.14)

Выражение (3.14) носит название нормальной числовой апертуры стекловолокна. Согласно рисунков 3.11 и 3.12, при g < g_К в окрестности точки B имеет место ПВО, и свет распространяется вдоль СВ по зигзагообразной траектории. При g > g_К условие ПВО не выполняется, и энергия волны 3 постепенно переводится в оболочку.

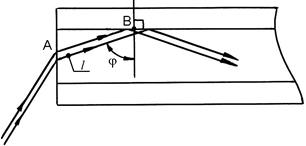
Рисунок 3.12 – К определению цифровой апертуры